Imaginary Numbers

reply to post by QuantumCounterfeit64

Yet. Debt is negative balance

You seem to be unable to distinguish between a concept and a tangible thing. A negative balance is typically a representation of a 32 bit integer stored on a PC. Debt is purely a concept, there is no actual negative dollar bills circulating around is there. Think carefully about what you are saying and then get back to us.

Originally posted by QuantumCounterfeit64

Originally posted by vind21

Originally posted by QuantumCounterfeit64
reply to post by ChaoticOrder

 

You said negative numbers cannot exist. Yet. If I owe someone 5 dollars whether I pay them back or not I still have -5 dollars. Because I still owe them until it's paid back. If you have an atom and you take away 5 neutrons and it's supposed to have 10. It is negative 5 neutrons even with the positive 5.

Root point though we can't visually observe negative numbers they do exist.

This is not correct. If you owe someone 5 dollars, you have "debt" which is a thing. You have purchased that debt with your 5 dollars or you have created an action that generated debt.

Is you take away 5 neutrons from an atom you end up with a radio active isotope.

Negative numbers are an idea, they precit the future or they describe a state of imbalance at best. That is why "when you get a negative number as an aswner, it's wrong"

edit on 11-6-2013 by vind21 because: (no reason given)

Your argument is flawed. Either you don't comprehend that debt is being in a negative area or you are just trying to look smarter then you've previously shown. Alot of people when they feel inadequate around someone they open there mouth to try to show to a observing group that they are either above or equivalent. I notice this is common on this site.

For example in the op the argument was presented that negative numbers don't exist. Yet. Debt is negative balance. Foreclosures on houses!!! You owe money You lose possessions. Negative. If I'm supposed to have 2 lungs and 1 gets removed I'm -1 lung. Plain and simple.

If someone makes a good point the argument moves to like it has that it still means nothing when talking about imaginary numbers. Ok so then why was the argument made int he first place? Why are we moving that argument out of the conversation?

So now when we move to what matters does it really matter int he first place because reality doesn't exist anyway it's just a dream! A creation of hallucinogenic chemicals in the brain. So infact nothing exists.

I don't even know how to reply to this...

If you have two lungs and you loose a lung, then you have 1 lung....that's called subtraction.

If I had 2 lungs and lost 2 lungs, I would have 0 lungs.

If I have 500 dollars and loose 600 dollars gambling, I still only have 0 dollars. I am in debt for 100 dollars, which is a description of a future event where I will loose 100 dollars once I accumulate more dollars.

reply to post by ChaoticOrder


I've actually already replied to this before it was wrote. i agreed you can't actually own something that's negative.

Originally posted by QuantumCounterfeit64
reply to post by ChaoticOrder

 

I've actually already replied to this before it was wrote. i agreed you can't actually own something that's negative.

Great, so then we're back to square one. Of course a negative balance can exist, no one is disputing negative as a mathematical concept. The point here is attempting to show examples of negativity in the physical world.

Originally posted by QuantumCounterfeit64
reply to post by vind21

 

You can own a negative balance that automatically gets deducted from any positive balance you deposit. Sure you can't own -1 dollar. But you are still -1 dollar.

That is still basic subtration.....OK maybe in banker world, and on the small level you are relating to, the anaolgy works.

Your still saying that your employer is negative xxxx$ becasue they have to pay you for your work, and still talking about basic subtraction. Or the fulfilment of a future condition.

And why has no one chimed in and given a black hole as an example of a negative exsistance...?

reply to post by vind21


I agree black hole! The color black, Shadows, Empty jars.

Originally posted by ChaoticOrder

Originally posted by QuantumCounterfeit64
reply to post by ChaoticOrder

 

I've actually already replied to this before it was wrote. i agreed you can't actually own something that's negative.

Great, so then we're back to square one. Of course a negative balance can exist, no one is disputing negative as a mathematical concept. The point here is attempting to show examples of negativity in the physical world.

I agree black hole! The color black, Shadows, Empty jars.

Im going to assume you were "joking" once again quantum....


How about electric current? That's still not the absence of a thing, but it could at least be a description of a negative number.

The idea of negative numbers was often considered suspect even into the 1800's. I've read a book by a mathematician of that time trying to present algebra in a way that didn't treat negative numbers as
real; he called them fictitious, and presented them as just a shorthand for operations that should properly be done in reverse. But e admitted that using negative numbers made the work easier, always gave the right answer (when interpreted correctly), and unified what would otherwise have required several cases (depending
on which number is greater, for example). That is, negative numbers serve as a good, though imperfect, MODEL--you don't have to recognize the existence of the negative numbers themselves as concrete entities
in order to make good use of them. (And, by the way, even counting numbers are really an abstract concept too--you never saw a "three" by itself, did you? ALL numbers live in the math world, not the real one.)

What we are doing when we use negative numbers is translating a real problem into a problem about, say, ocations on a number line (which correspond to amounts of money you have or owe, say), solving that new problem, and then deciding how to translate the answer back into the real world problem. The negative numbers live in this separate world of math, and may have various meanings or lack of meaning in the real world

reply to post by vind21

The idea of negative numbers was often considered suspect even into the 1800's. I've read a book by a mathematician of that time trying to present algebra in a way that didn't treat negative numbers as
real; he called them fictitious, and presented them as just a shorthand for operations that should properly be done in reverse. But e admitted that using negative numbers made the work easier, always gave the right answer (when interpreted correctly), and unified what would otherwise have required several cases (depending
on which number is greater, for example). That is, negative numbers serve as a good, though imperfect, MODEL--you don't have to recognize the existence of the negative numbers themselves as concrete entities
in order to make good use of them. (And, by the way, even counting numbers are really an abstract concept too--you never saw a "three" by itself, did you? ALL numbers live in the math world, not the real one.)

That is the point I was making about both negative and imaginary numbers in the opening post. Imaginary numbers can be thought of as an algebraic tool which completes algebra system and allows us to solve any algebra equation, even if the answer is an imaginary number.

However I was alluding to the fact that negativity does seem to have a physical manifestation, in the form of negative energy, and it can help explain the origins of the universe. Read something by Hawking on the topic of negative energy or watch a lecture on the topic by Lawrence Krauss. I took that point and used it to suggest that imaginary numbers may also have a real world basis, even if subtle like negative energy, based on the fact that we can use imaginary numbers to solve all sorts of complex problems which go right to the heart of reality.

reply to post by ChaoticOrder


I disagree with hawking most of the time. If you have read some of my other threads you know that I am much more inclined with EU than GR.

In 1948 Dutch physicist Hendrik B. G. Casimir showed that two uncharged parallel metal plates alter the vacuum fluctuations in such a way as to attract each other. The energy density between the plates was later calculated to be negative. In effect, the plates reduce the fluctuations in the gap between them; this creates negative energy and pressure, which pulls the plates together.

The Casimir effect has recently been measured by Steve K. Lamoreaux of Los Alamos National Laboratory and by Umar Mohideen of the University of California at Riverside and his colleague Anushree Roy. Similarly, in the 1970s Paul C. W. Davies and Stephen A. Fulling, then at King’s College at the University of London, predicted that a moving boundary, such as a moving mirror, could produce a flux of negative energy.


For both the Casimir effect and squeezed states, researchers have measured only the indirect effects of negative energy.


Even in the case of negative energy, a postive result is produced....if negative energy can still produce work, is it really negative? Or do we jsut have a really bad example as our baseline observation? It could be that humans, are just bad at math.

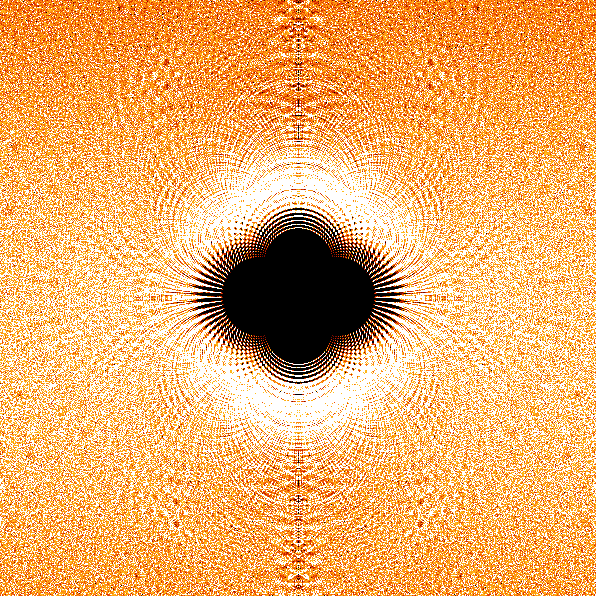
john baez: algebraic roots

the image here is a color density plot of the solutions of all polynomials in the vicinity of 'i'. i highly recommend reading the link and checking out the other images of the solution space.

imaginary numbers are completely valid and widely accepted. the idea was mathematically formalized by Clifford, and is of necessity a geometric concept. in other words, it makes little use to try to make sense of this type of number outside of the pythagorean identity (a^2 +b^2 = c^2).

of further interest are the set of hypernumbers, which are a very fringe mathematical concept.

reply to post by ChaoticOrder


Just looks like a more complicated math to me (multilayered). They can't be imaginary numbers if they have real world uses.
Maths therefore is incomplete.

reply to post by vind21

Even in the case of negative energy, a postive result is produced....if negative energy can still produce work, is it really negative?

I can see the point you are getting at but I think what you have said is a generalization of what actually happens. Just because positive energy is produced alone with some sort of negative energy doesn't make it strange. But I'm certainly not an expert on negative energy and the way it works so I don't have an exact answer to any of this. Anyway I'm quite tired and my brain isn't working properly so I'll check back on this thread later after I'd had a bit of sleep.

reply to post by tgidkp


Coolest post of the day award!



And yes, everything I have been saying are generalizations and real world actions that are best described by imaginary numbers. I wouldn't try to read into it to much.

reply to post by ManFromEurope

I've always preferred it when written as e^-(i*π) +1 = 0

You get all the main operands (addition, multiplication, and exponents), as well as 1 and 0, i, and a couple of irrational constants to boot! The only thing really missing is infinity.

Seems more all-encompassing and symmetrical to me in that form.

reply to post by ChaoticOrder


Maybe theses values relate to the existence of 3 dimensions, and also value increasing over the dimension of time? Like left is -1. Right is +1. up is i. down is + i. Or something like that (I have minimal math experience so am just throwing out thoughts in hopes to maybe give you an idea), and so the different changing of a value moving through a 3-d plane perhaps there are inherent qualities of space, which cause a particle to not give its intrinsic energetic and charge and spin properties to the space that surrounds it. because maybe space is purely space and nuetral. this could relate to particles traveling in waves. Because there are always values surrounding a particle, whether gravity or attraction or repulsion, or EM radiation, or dark matter or energy, surrounding a traveling particle, there are fluxing of energy levels, so perhaps after a particle is released from an environment, that enivronments surrounding fluxes are imparted on the particles trajectory, which the particle keeps, and this is the particles wave function. and perhaps this wave function because it is vibrating and swirling and waving in 3-d perhaps the troughs and crests and horizontal vibes can be represented with i,-i,1,+1. And the starting from a value, the system progresses over time, and so that is why the number values exponentially get bigger, because its a plotting of a value moving through space, and over time.

Also maybe how negative numbers and imaginary numbers relate to reality have to do with some mysterious circumstances surrounding anti matter, like the 'back in time' theories, and even why and how it exists. Also maybe relating to the idea behind energy cannot be created or destroyed and entropy, recycling, order. The number line needs dimension perhaps, or the fact that a single value can do multiple things, be used for multiple things, change directions, change velocity, impart velocity to multiple objects, do complex swirling and looping patterns with different velocity then its neighboring objects. Idk. Intriguing OP though

It's simpler than it sounds. i is basically a polarity flipper. Also, it's perhaps better to think of numbers like these in terms of distances, not quantities. It's easier to imagine a negative distance than a negative quantity. Distance is always relative, while quantity is usually absolute (neither +/-).

I find it easier to understand i when we break down our understanding of square roots a bit.
Example: 2 is the square root of 4, because 2*2=4. Note the following expressions:
+2 * +2 = +4
-2 * -2 = +4
+2 * -2 = -4
-2 * +2 = -4

When we get the square root of 4 we default to a single answer when in fact a dual answer would be more appropriate. Both +2 and -2 are the root of +4, because either one times itself = +4. But since a single result is expected, in order to get the root of -4 we use i to flip the polarity during the expression.

I think it's kinda dumb personally that dual answers aren't the norm with roots. I'm guessing it's because roots & negative numbers developed separately from each other. Then they met and had a baby named i.

Imaginary numbers, despite their name, have a very real location as it relates to the unit circle and trigonometry. Otherwise the circle wouldn't be whole.

reply to post by circlemaker

But since a single result is expected, in order to get the root of -4 we use i to flip the polarity during the expression.

That's what I was getting at when I mentioned that our operators don't apply the same way to imaginary numbers because of the way i shifts through negative and positive values when taken to the power of n. But it's not just polarity shifting, the numbers can also shift between real and imaginary numbers. For example an imaginary number multiplied by an imaginary number seems to result in a real number, however a real number multiplied by an imaginary number seems to give an imaginary number. So When you do i^2 you're really saying (i x i), which gives a real number of -1. However if you do i^3 then it's the result of i^2 multiplied by i, and the result of i^2 is a real number. So we switch back to imaginary numbers again, and the result of i^3 is -i.

When you multiply a real number by an imaginary number you simply change the magnitude of the imaginary number but you don't make it real and don't make it shift polarity (eg. -1 x i = -i). But a good example of how the polarity flipping works is when you multiply an imaginary number by another imaginary number. So for example i^4 is (-i x i) and the result is a real number of course, but it's not -1, the answer is positive 1. So unlike normal numbers, a negative imaginary number multiplied by a positive imaginary number will result in a positive real number. The sign has been shifted in the opposite way as normal.

Originally posted by vind21
Hmmm.....

Is there a reason I feel like im being led to a conversation about dipoles?

Well, no. A dipole is a structure with a positive and negative charge - like, say, a proton and electron.

By standard rules.....does this not describe an ionizing magnetic field? Or possibly the negative portion of a dipole? A monopole?

Magnetic fields don't ionize. The negative portion of a dipole is usually an electron. Electric charges are monopoles. It's questionable if magnets have monopoles.

Originally posted by ManFromEurope
e^-(i*Pi) = -1

The freaking most beautiful equation in the universe!

e and ln are pretty oddball the first time you see them too.