It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
share:
NOTE: if you haven't heard of imaginary numbers or complex numbers, I would suggest doing a quick Google or YouTube search and familiarizing yourself
with this topic at least a little bit bit before you attempt to read this thread. A great starting point for the beginner is
this page.
This is a topic which, although extremely interesting, hasn't received much attention from ATS members and researchers. One reason for this is probably because the topic is so complex and abstract, not to mention most mathematicians will admit we know barely anything about imaginary numbers or whether they really even exist. Some people argue we shouldn't even use them because they are made up nonsense with no basis in reality.
However one might also argue that negative numbers have no basis in reality because you can't have "negative something". Yet clearly mathematicians agree that negative numbers are "real" because they can easily be visualized, where as it's supposedly impossible to visualize an imaginary unit. Now, I think it's important to consider what "negative something" really means. When you think about it, the phrase "something" can be reduced to "matter".
According to Einstein we can really just think of matter as one possible form of energy. In fact modern cosmology is quickly adopting the concept of "negative energy". There are theories which predict the total amount of energy in the universe is 0 because all the negative energy cancels out all the positive energy. In essence the theory is an attempt to answer the question of why does something exist rather than nothing.
So there may in fact be a physical manifestation of "negative energy" which only further confirms the mathematical foundations of reality. When you realize that all particles are really particle-waves and can be expressed with a wave function you realize just how math-based our reality is. So getting back to the main topic at hand... what does any of this have to do with imaginary numbers you ask? Well it should be obvious.
Perhaps these imaginary numbers aren't so imaginary after all and they really do have some basis in reality. After all, imaginary numbers are crucial to electronic engineering and quantum mechanics. These so called imaginary numbers also appear to have a basis in the real world, which is quite extraordinary if you ask me. Consider the reasons for why we started to use imaginary numbers in the first place.
It was to fill a gap, a discrepancy between what we could express algebraically and what we could solve algebraically. Put simply: we had equations which were impossible to solve without introducing imaginary numbers. For example the square root of -1 or any negative number for that matter cannot be solved without imaginary numbers. Now it's obvious why the square root of -1 cannot be solved if you think about it.
The square root is the opposite of the square of a number, so to find the square root you must find a number which when multiplied by itself equals the number you are looking for the square root of. However, any positive number multiplied by its self equals a positive number and any negative number multiplied by its self equals a positive number. There is absolutely no number on the real number line which is the square root of -1.
This is why many people argue against the use of imaginary numbers, their use violates the known rules of mathematics and introduces units which shouldn't even exist. However there was also a time when any solution to an equation which resulted in a negative number was considered to be the "wrong" answer. It's important to keep in mind that imaginary numbers are merely an algebraic tool to solve equations, and the rules for using them work.
However, the algebraic tool required is an "extra-dimensional" number system which exists outside of the real number line and contains all the imaginary numbers. Now what is the real number line? Well imagine 0-dimensions as a point with no width, height, or depth. Now if we give our point width it becomes a 1-dimensional line. The real number line is simply a 1-dimension line which extends infinitely in both directions.
We pick an arbitrary point on the line and call it 0. To the left of 0 we have the negative range of numbers and to the right of 0 we have the positive range of numbers, extending to infinity of course. So we can clearly visualize negative numbers in this way. On the other hand we cannot visualize imaginary numbers in a similar way. Now the next step would be to stretch the line out vertically and give it height, creating a 2-dimensional surface.
At this point you might be thinking "well what about the complex plane, that's a 2D plane with an imaginary axis and a real axis and it gives us a way to visualize imaginary numbers". My response to that thinking would be that you are confused, the complex plane plots complex numbers, and complex numbers have both a real part and an imaginary part. That is not the same thing as plotting out the structure of an imaginary number.
The spacings on the imaginary line are completely arbitrary and mean nothing because we have no way of visualizing an imaginary quantity. The expression (2i < 3i) is not even necessary true. If imaginary numbers really are some type of multi-dimensional numbers with multiple components, like a vector with 2 components, we should be able to apply simple vector math to them and also visualize them in a nice way.
You might say all real numbers would exist on the "event horizon" of the imaginary number space, meaning that all real numbers would have a y component equal to 0. However there is no vector which when multiplied by itself results in a vector where x=-1 and y=0 (aka the real number -1). We run into the same problem, a negative vector multiplied with a negative vector is a positive vector. I wish it were that easy, but if it were it would have been figured out already.
There is a deeper secret to the mystery of the imaginary numbers. Personally I don't believe imaginary numbers represent a multi-dimensional number. The math just doesn't work out any way you try it, these numbers don't appear to operate like normal numbers. In fact the answer may be that our mathematical operators apply differently to imaginary numbers. It's the only way to actually reach the square root of -1 when you think about it.
i^2 = i x i = -1
i^3 = -1 x i = -i
i^4 = -i x i = 1
i^5 = 1 x i = i
The pattern above will repeat on, so i^6 is -1 and i^7 is -i, and so on. Now think about how absurd that is. You can take the real number 1 to the power of anything and the answer will always be one, but with the imaginary unit that is not the case. Each time we multiply i by itself we shift through negative and positive, real and imaginary values. It's as if each exponential operation on the imaginary number has some sort of repeating recursive behavior causing it to shift between real and imaginary.
The only way we can explain this and possibly hope to visualize imaginary numbers is to understand and define the strange operational rules that apply to imaginary numbers. Perhaps a good analogy might be to picture another universe where the laws of physics behave completely differently. It appears that we have inadvertently stumbled across a new universe of numbers where our old rules don't apply the same way.
And yet the most mysterious thing is that these imaginary numbers seem to have a real world manifestation and basis in reality. One must question whether our mathematical rules are incomplete or built on a faulty premise. If we have missed something important the mysterious world of imaginary numbers may just be the road to completing our understanding of mathematics, and thusly understanding the true nature of reality.
This is a topic which, although extremely interesting, hasn't received much attention from ATS members and researchers. One reason for this is probably because the topic is so complex and abstract, not to mention most mathematicians will admit we know barely anything about imaginary numbers or whether they really even exist. Some people argue we shouldn't even use them because they are made up nonsense with no basis in reality.
However one might also argue that negative numbers have no basis in reality because you can't have "negative something". Yet clearly mathematicians agree that negative numbers are "real" because they can easily be visualized, where as it's supposedly impossible to visualize an imaginary unit. Now, I think it's important to consider what "negative something" really means. When you think about it, the phrase "something" can be reduced to "matter".
According to Einstein we can really just think of matter as one possible form of energy. In fact modern cosmology is quickly adopting the concept of "negative energy". There are theories which predict the total amount of energy in the universe is 0 because all the negative energy cancels out all the positive energy. In essence the theory is an attempt to answer the question of why does something exist rather than nothing.
So there may in fact be a physical manifestation of "negative energy" which only further confirms the mathematical foundations of reality. When you realize that all particles are really particle-waves and can be expressed with a wave function you realize just how math-based our reality is. So getting back to the main topic at hand... what does any of this have to do with imaginary numbers you ask? Well it should be obvious.
Perhaps these imaginary numbers aren't so imaginary after all and they really do have some basis in reality. After all, imaginary numbers are crucial to electronic engineering and quantum mechanics. These so called imaginary numbers also appear to have a basis in the real world, which is quite extraordinary if you ask me. Consider the reasons for why we started to use imaginary numbers in the first place.
It was to fill a gap, a discrepancy between what we could express algebraically and what we could solve algebraically. Put simply: we had equations which were impossible to solve without introducing imaginary numbers. For example the square root of -1 or any negative number for that matter cannot be solved without imaginary numbers. Now it's obvious why the square root of -1 cannot be solved if you think about it.
The square root is the opposite of the square of a number, so to find the square root you must find a number which when multiplied by itself equals the number you are looking for the square root of. However, any positive number multiplied by its self equals a positive number and any negative number multiplied by its self equals a positive number. There is absolutely no number on the real number line which is the square root of -1.
This is why many people argue against the use of imaginary numbers, their use violates the known rules of mathematics and introduces units which shouldn't even exist. However there was also a time when any solution to an equation which resulted in a negative number was considered to be the "wrong" answer. It's important to keep in mind that imaginary numbers are merely an algebraic tool to solve equations, and the rules for using them work.
However, the algebraic tool required is an "extra-dimensional" number system which exists outside of the real number line and contains all the imaginary numbers. Now what is the real number line? Well imagine 0-dimensions as a point with no width, height, or depth. Now if we give our point width it becomes a 1-dimensional line. The real number line is simply a 1-dimension line which extends infinitely in both directions.
We pick an arbitrary point on the line and call it 0. To the left of 0 we have the negative range of numbers and to the right of 0 we have the positive range of numbers, extending to infinity of course. So we can clearly visualize negative numbers in this way. On the other hand we cannot visualize imaginary numbers in a similar way. Now the next step would be to stretch the line out vertically and give it height, creating a 2-dimensional surface.
At this point you might be thinking "well what about the complex plane, that's a 2D plane with an imaginary axis and a real axis and it gives us a way to visualize imaginary numbers". My response to that thinking would be that you are confused, the complex plane plots complex numbers, and complex numbers have both a real part and an imaginary part. That is not the same thing as plotting out the structure of an imaginary number.
The spacings on the imaginary line are completely arbitrary and mean nothing because we have no way of visualizing an imaginary quantity. The expression (2i < 3i) is not even necessary true. If imaginary numbers really are some type of multi-dimensional numbers with multiple components, like a vector with 2 components, we should be able to apply simple vector math to them and also visualize them in a nice way.
You might say all real numbers would exist on the "event horizon" of the imaginary number space, meaning that all real numbers would have a y component equal to 0. However there is no vector which when multiplied by itself results in a vector where x=-1 and y=0 (aka the real number -1). We run into the same problem, a negative vector multiplied with a negative vector is a positive vector. I wish it were that easy, but if it were it would have been figured out already.
There is a deeper secret to the mystery of the imaginary numbers. Personally I don't believe imaginary numbers represent a multi-dimensional number. The math just doesn't work out any way you try it, these numbers don't appear to operate like normal numbers. In fact the answer may be that our mathematical operators apply differently to imaginary numbers. It's the only way to actually reach the square root of -1 when you think about it.
i^2 = i x i = -1
i^3 = -1 x i = -i
i^4 = -i x i = 1
i^5 = 1 x i = i
The pattern above will repeat on, so i^6 is -1 and i^7 is -i, and so on. Now think about how absurd that is. You can take the real number 1 to the power of anything and the answer will always be one, but with the imaginary unit that is not the case. Each time we multiply i by itself we shift through negative and positive, real and imaginary values. It's as if each exponential operation on the imaginary number has some sort of repeating recursive behavior causing it to shift between real and imaginary.
The only way we can explain this and possibly hope to visualize imaginary numbers is to understand and define the strange operational rules that apply to imaginary numbers. Perhaps a good analogy might be to picture another universe where the laws of physics behave completely differently. It appears that we have inadvertently stumbled across a new universe of numbers where our old rules don't apply the same way.
And yet the most mysterious thing is that these imaginary numbers seem to have a real world manifestation and basis in reality. One must question whether our mathematical rules are incomplete or built on a faulty premise. If we have missed something important the mysterious world of imaginary numbers may just be the road to completing our understanding of mathematics, and thusly understanding the true nature of reality.
edit on
11/6/2013 by ChaoticOrder because: (no reason given)
Hmmm.....
Is there a reason I feel like im being led to a conversation about dipoles?
By standard rules.....does this not describe an ionizing magnetic field? Or possibly the negative portion of a dipole? A monopole?
I mean, I guess it's a stretch to say the square of -1 = i = -i is a monopole, but, just saying, they are oddly related concepts.
Wiki:
A magnetic monopole is a hypothetical particle in particle physics that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice-versa). In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence.
Magnetism in bar magnets and electromagnets does not arise from magnetic monopoles, and in fact there is no conclusive experimental evidence that magnetic monopoles exist at all in the universe.
To be precise: for the definition of the dipole moment one should always consider the "dipole limit", where e.g. the distance of the generating charges should converge to 0, while simultaneously the charge strength should diverge to infinity in such a way that the product remains a positive constant.
Is there a reason I feel like im being led to a conversation about dipoles?
By standard rules.....does this not describe an ionizing magnetic field? Or possibly the negative portion of a dipole? A monopole?
I mean, I guess it's a stretch to say the square of -1 = i = -i is a monopole, but, just saying, they are oddly related concepts.
Wiki:
A magnetic monopole is a hypothetical particle in particle physics that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice-versa). In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence.
Magnetism in bar magnets and electromagnets does not arise from magnetic monopoles, and in fact there is no conclusive experimental evidence that magnetic monopoles exist at all in the universe.
To be precise: for the definition of the dipole moment one should always consider the "dipole limit", where e.g. the distance of the generating charges should converge to 0, while simultaneously the charge strength should diverge to infinity in such a way that the product remains a positive constant.
edit on 11-6-2013 by vind21 because: (no reason given)
e^-(i*Pi) = -1
The freaking most beautiful equation in the universe!
Source of course
Edit: Sorry for the f*-word, but its xkcd! XKCD! Honor that!
The freaking most beautiful equation in the universe!
Source of course
Edit: Sorry for the f*-word, but its xkcd! XKCD! Honor that!
edit on 11-6-2013 by ManFromEurope because: (no reason given)
reply to post by vind21
i^2 = -1 and i -i
And I also don't really see how this relates to monopoles given that your above assertions are incorrect.
i^2= -i
...
-1 = i = -i
i^2 = -1 and i -i
And I also don't really see how this relates to monopoles given that your above assertions are incorrect.
edit on 11/6/2013 by ChaoticOrder
because: (no reason given)
They are very useful in the expression of electromagnetic waves. In other words, they work. In fact they don't just work, they are indispensable for
any number of RF applications many take for granted.
Pure conjecture:
Conceptually, imaginary numbers could represent an additional dimension of the universe that we express in mathematics which is (essentially) counting quanta in 4 dimensions. The oscillating i axis could be 5 (or 4.5) dimensional geometry projected in 4 dimensions. We don't currently have an extra-dimensional model that is "solid" yet. I believe science is getting closer.
Opinion:
I don't think quantum entanglement is "spooky" at all. I just don't think we understand the geometry of space yet.
Pure conjecture:
Conceptually, imaginary numbers could represent an additional dimension of the universe that we express in mathematics which is (essentially) counting quanta in 4 dimensions. The oscillating i axis could be 5 (or 4.5) dimensional geometry projected in 4 dimensions. We don't currently have an extra-dimensional model that is "solid" yet. I believe science is getting closer.
Opinion:
I don't think quantum entanglement is "spooky" at all. I just don't think we understand the geometry of space yet.
reply to post by ManFromEurope
I prefer tau over pi myself:
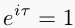
I prefer tau over pi myself:
edit on 11/6/2013 by ChaoticOrder because: (no reason given)
reply to post by ChaoticOrder
I find the concept of imaginary numbers fascinating. In your example you point out situations that arise with positive and negative numbers when considering "powers". However, you could also have imaginary number systems with other "odd" behaviors. For instance, consider a number system where 1 + 1 does equal 3 - possible in your imaginary number system.
Try creating other number systems with alternative behaviors. Then try doing basic math and see how your new number system behaves. Can you graphing your results? You may discover a new way of looking at math and its place in the universe.
I find the concept of imaginary numbers fascinating. In your example you point out situations that arise with positive and negative numbers when considering "powers". However, you could also have imaginary number systems with other "odd" behaviors. For instance, consider a number system where 1 + 1 does equal 3 - possible in your imaginary number system.
Try creating other number systems with alternative behaviors. Then try doing basic math and see how your new number system behaves. Can you graphing your results? You may discover a new way of looking at math and its place in the universe.
using something as simple as a wave, it's easy to see how negative values have importance. It's not the absence of something, it has to do with
where the base is located. We locate it at zero with positive and negative infinity on each side. It's not a matter of a negative value, merely a
negative position. Imaginary numbers just signify root functions involving numbers in a negative position. Think in terms of vectors as opposed to
scalars.
reply to post by InverseLookingGlass
That is an extremely fascinating concept, although I think I've heard a similar idea described some where before. My thinking would be along the same lines as you on this. If we are required to invent new math to make our physics equations work nicely it should be saying something to us about the nature of reality. There seems to be some sort of hidden dimension(s) which contribute to the way the laws of physics work in our dimension and we are describing this hidden dimension indirectly through imaginary numbers and complex numbers.
Conceptually, imaginary numbers could represent an additional dimension of the universe that we express in mathematics which is (essentially) counting quanta in 4 dimensions.
That is an extremely fascinating concept, although I think I've heard a similar idea described some where before. My thinking would be along the same lines as you on this. If we are required to invent new math to make our physics equations work nicely it should be saying something to us about the nature of reality. There seems to be some sort of hidden dimension(s) which contribute to the way the laws of physics work in our dimension and we are describing this hidden dimension indirectly through imaginary numbers and complex numbers.
reply to post by ChaoticOrder
There seems to be some sort of hidden dimension(s) which contribute to the way the laws of physics work in our dimension and we are describing this hidden dimension indirectly through imaginary numbers and complex numbers.
Sorry I typo'd the first one, and changed to -1= i = -i saying that if a negative number can equal an imaginary number, it must also be equal to a negative imaginary number. I was not giving a value for i directly, sorry for the horrible explination. I would leave out any value for i and simply focus on the "state" of the number, being positive or negative.
I would argue that if I can multiply two real positive number together and achive the same state, I should be able to multiply two negative real numbers together and achive the same state. This is not any more ludicrious than the use of relativity to describe a universe with no mass. IE does the exsistance of imaginary numbers and thier pratical application in quantum mechanics quietly insist a duality to the universe we have yet to understand.
Dipoles relate directly to this subject on the basis of EMF and is the only place were imaginary numbers are used in a practical application. This is why I was wondeing if you were leading us in that direction. The quote above from you is what I was thinking you were getting at.
edit on 11-6-2013 by vind21 because: (no reason given)
edit on 11-6-2013 by vind21 because: (no reason given)
reply to post by JacobsLadder
Yes that is a good point and I was going to say a few words on that but decided to skip over it. However I would point out that if you want to consider the concept of physical existence and energy, you have to consider the state of nothing as the base point.
using something as simple as a wave, it's easy to see how negative values have importance. It's not the absence of something, it has to do with where the base is located.
Yes that is a good point and I was going to say a few words on that but decided to skip over it. However I would point out that if you want to consider the concept of physical existence and energy, you have to consider the state of nothing as the base point.
reply to post by ChaoticOrder
You said negative numbers cannot exist. Yet. If I owe someone 5 dollars whether I pay them back or not I still have -5 dollars. Because I still owe them until it's paid back. If you have an atom and you take away 5 neutrons and it's supposed to have 10. It is negative 5 neutrons even with the positive 5.
Root point though we can't visually observe negative numbers they do exist.
You said negative numbers cannot exist. Yet. If I owe someone 5 dollars whether I pay them back or not I still have -5 dollars. Because I still owe them until it's paid back. If you have an atom and you take away 5 neutrons and it's supposed to have 10. It is negative 5 neutrons even with the positive 5.
Root point though we can't visually observe negative numbers they do exist.
Originally posted by QuantumCounterfeit64
reply to post by ChaoticOrder
You said negative numbers cannot exist. Yet. If I owe someone 5 dollars whether I pay them back or not I still have -5 dollars. Because I still owe them until it's paid back. If you have an atom and you take away 5 neutrons and it's supposed to have 10. It is negative 5 neutrons even with the positive 5.
Root point though we can't visually observe negative numbers they do exist.
This is not correct. If you owe someone 5 dollars, you have "debt" which is a thing. You have purchased that debt with your 5 dollars or you have created an action that generated debt.
Is you take away 5 neutrons from an atom you end up with a radio active isotope.
Negative numbers are an idea, they precit the future or they describe a state of imbalance at best. That is why "when you get a negative number as an aswner, it's wrong"
edit on 11-6-2013 by vind21 because: (no reason given)
reply to post by vind21
I would rephrase that to say debt is a concept, not a thing. But the gist of what you are saying is correct.
you have "debt" which is a thing.
I would rephrase that to say debt is a concept, not a thing. But the gist of what you are saying is correct.
reply to post by ChaoticOrder
thing, concept, idea.... its all the same in the end.
a thing = concept = -idea hehe i = 1 = -i
thing, concept, idea.... its all the same in the end.
a thing = concept = -idea hehe i = 1 = -i
reply to post by vind21
I would beg to differ. The whole premise of your argument relies on a distinction between a concept and a real physical thing. A debt is a concept and therefore not a physical example of something being truly negative.
If you accept that, you accept negative numbers and nothing more. That still doesn't help anyone accept imaginary numbers because they are a whole other thing which exist outside of the real number line.
thing, concept, idea.... its all the same in the end.
I would beg to differ. The whole premise of your argument relies on a distinction between a concept and a real physical thing. A debt is a concept and therefore not a physical example of something being truly negative.
A negative number can only exsist in refference to a positive one. If you acept that, you can easily acept imaginary numbers.
If you accept that, you accept negative numbers and nothing more. That still doesn't help anyone accept imaginary numbers because they are a whole other thing which exist outside of the real number line.
Originally posted by vind21
Originally posted by QuantumCounterfeit64
reply to post by ChaoticOrder
You said negative numbers cannot exist. Yet. If I owe someone 5 dollars whether I pay them back or not I still have -5 dollars. Because I still owe them until it's paid back. If you have an atom and you take away 5 neutrons and it's supposed to have 10. It is negative 5 neutrons even with the positive 5.
Root point though we can't visually observe negative numbers they do exist.
This is not correct. If you owe someone 5 dollars, you have "debt" which is a thing. You have purchased that debt with your 5 dollars or you have created an action that generated debt.
Is you take away 5 neutrons from an atom you end up with a radio active isotope.
Negative numbers are an idea, they precit the future or they describe a state of imbalance at best. That is why "when you get a negative number as an aswner, it's wrong"edit on 11-6-2013 by vind21 because: (no reason given)
Your argument is flawed. Either you don't comprehend that debt is being in a negative area or you are just trying to look smarter then you've previously shown. Alot of people when they feel inadequate around someone they open there mouth to try to show to a observing group that they are either above or equivalent. I notice this is common on this site.
For example in the op the argument was presented that negative numbers don't exist. Yet. Debt is negative balance. Foreclosures on houses!!! You owe money You lose possessions. Negative. If I'm supposed to have 2 lungs and 1 gets removed I'm -1 lung. Plain and simple.
If someone makes a good point the argument moves to like it has that it still means nothing when talking about imaginary numbers. Ok so then why was the argument made int he first place? Why are we moving that argument out of the conversation?
So now when we move to what matters does it really matter int he first place because reality doesn't exist anyway it's just a dream! A creation of hallucinogenic chemicals in the brain. So infact nothing exists.
Originally posted by ChaoticOrder
reply to post by vind21
thing, concept, idea.... its all the same in the end.
I would beg to differ. The whole premise of your argument relies on a distinction between a concept and a real physical thing. A debt is a concept and therefore not a physical example of something being truly negative.
A negative number can only exsist in refference to a positive one. If you acept that, you can easily acept imaginary numbers.
If you accept that, you accept negative numbers and nothing more. That still doesn't help anyone accept imaginary numbers because they are a whole other thing which exist outside of the real number line.
Ok ok, one second... do we both agree you can never have "negative" anything? That is to say I cannot have negative cars in my drive way, we can never have "negative" physiacal objects?
edit on 11-6-2013 by vind21 because: (no reason given)
reply to post by vind21
For the most part, yes, we are saying the same thing. However, I would say you can have negative energy in the same way Stephen Hawking would say you can have negative energy.
Ok ok, one second... do we both agree you can never have "negative" anything? That is to say I cannot have negative cars in my drive way, we can never have "negative" physiacal objects?
For the most part, yes, we are saying the same thing. However, I would say you can have negative energy in the same way Stephen Hawking would say you can have negative energy.
reply to post by vind21
You can own a negative balance that automatically gets deducted from any positive balance you deposit. Sure you can't own -1 dollar. But you are still -1 dollar.
You can own a negative balance that automatically gets deducted from any positive balance you deposit. Sure you can't own -1 dollar. But you are still -1 dollar.
new topics
-
Christianity superior to other faiths for very specific reasons. Awaken to true FREEDOM..!!
Conspiracies in Religions: 4 minutes ago -
It's all Kicking off at Eurovision 2024
Music: 4 hours ago -
The biggest problem with the Hush money trial
US Political Madness: 5 hours ago -
Armadillos moving north
Fragile Earth: 8 hours ago -
Million dollar idea, and good for your feelz!
Rant: 8 hours ago -
Is there a dependence on the number of children in the family and its well-being?
New World Order: 8 hours ago
top topics
-
Armadillos moving north
Fragile Earth: 8 hours ago, 6 flags -
The biggest problem with the Hush money trial
US Political Madness: 5 hours ago, 5 flags -
Is Taco Bell Satanic?
Education and Media: 17 hours ago, 4 flags -
Barron Trump has prior commitments?
Politicians & People: 14 hours ago, 4 flags -
Million dollar idea, and good for your feelz!
Rant: 8 hours ago, 3 flags -
Is there a dependence on the number of children in the family and its well-being?
New World Order: 8 hours ago, 2 flags -
It's all Kicking off at Eurovision 2024
Music: 4 hours ago, 1 flags -
Christianity superior to other faiths for very specific reasons. Awaken to true FREEDOM..!!
Conspiracies in Religions: 4 minutes ago, 0 flags
active topics
-
The biggest problem with the Hush money trial
US Political Madness • 80 • : Annee -
Multipal Solar Storms Coming Our Way This Weekend
Fragile Earth • 38 • : Dalamax -
Christianity superior to other faiths for very specific reasons. Awaken to true FREEDOM..!!
Conspiracies in Religions • 0 • : FlyInTheOintment -
The geography of Eden
Religion, Faith, And Theology • 7 • : Station27 -
Barron Trump has prior commitments?
Politicians & People • 77 • : RickinVa -
-@TH3WH17ERABB17- -Q- ---TIME TO SHOW THE WORLD--- -Part- --44--
Dissecting Disinformation • 942 • : Thoughtful3 -
Russia Ukraine Update Thread - part 3
World War Three • 5774 • : Imhere -
Is there a dependence on the number of children in the family and its well-being?
New World Order • 36 • : RussianTroll -
Is Taco Bell Satanic?
Education and Media • 32 • : Ohanka -
Bibi’s Dilemma
Middle East Issues • 162 • : DBCowboy

