Refutation of the NIST-Bazant Collapse Hypothesis

This, 01-21-09, paper, points out 'critical' flaws in Bazant/NIST hypothesis....flaws that are blatantly obvious, and, hopefully, will help lead to criminal action. ..but, you do need to know how to read and have 'basic' math skills.....that kind of messes with most of you shills though....sorry!

read the paper

and before you say....NIST never said anything about a 'jolt',-

NCSTAR 1-6, pp. 416, 238, 196 “Since the stories below the level of collapse initiation provided little resistance to the tremendous energy released by the falling building mass, the building section above came down essentially in free fall, as seen in videos.”...“The potential energy released by the downward movement of the large building mass far exceeded the capacity of the intact structure below to absorb that through energy of deformation.”

Bazant said, "when the top part fell and struck the stories beneath it, there had to be a powerful jolt."

I think the "jolt" issue was addressed by Architects and Engineers for Truth in their video presentation on the destruction of the towers. No jolt. No deceleration of the upper portion.

When are the American people going to drag the perps out of their limos and down to the police station to be booked?

Originally posted by hgfbob
NCSTAR 1-6, pp. 416, 238, 196 “Since the stories below the level of collapse initiation provided little resistance to the tremendous energy released by the falling building mass, the building section above came down essentially in free fall, as seen in videos.”

That's funny. Here's the NIST team saying the WTC Towers "came down essentially in free fall, as seen in videos," yet there are clowns here who have convinced themselves that the collapses were "a lot" slower that free-fall. Not even NIST was that blindly biased, but then again, NIST actually fesses up to a lot more in their reports than people realize. It's mainly only their actual hypotheses (that they never tested) that contradict the data they present and go way out of line.

“The potential energy released by the downward movement of the large building mass far exceeded the capacity of the intact structure below to absorb that through energy of deformation.”

Even if this is assumed instantaneously, they can't say this is going to be the case for the entire collapse. It should definitely lose energy and slow down as it progresses further and further into intact structure that requires more and more energy to rip apart. And most of the mass was going straight out the sides in all directions, not straight down.

"It is also important to note here that Bazant was off by a factor of ten in his calculation of the stiffness of the columns, with his 71 GN/m estimate. [8] The actual stiffness, calculated here using the actual column cross sections, is approximately 7.1 GN/m. (see Appendices B and C)
[19][20] This error of Bazant’s caused him to significantly overestimate the potential amplifying effect of the impulse or jolt he claims occurred after a one story fall of the upper block."

paper

This alleged "refutation" was addressed by a few qualified structural engineers and scientists.

Jof911 Studies claim it is a "peer reviewed" paper. It is not.

Anyway, I thought I would share some of the comments regarding the latest paper from the Journal of 911 Studies.

Let's suppose, for sake of argument, we accept their argument, we accept their method, and we accept their data analysis -- we don't, of course, but just suppose -- and we agree with their conclusion that the upper block doesn't experience the "Big Jerk." What does this mean? The authors claim that it invalidates Bazant & Zhou's progressive collapse paper. But is this true?

We've discussed Bazant & Zhou any number of times here. The criticism generally concerns their model of the collapse, rather than the calculations themselves. In their model, an admittedly simplified one, a simplified, rigid upper block is dropped the height of one story onto a simplified lower block, under the influence of gravity (and slightly opposed by the collapsing story -- a small correction is included for columns considered to be at their yield point at the start of the trial). This leads to a big bang, which as they calculate, cannot possibly be resisted by the columns on the next floor. Therefore, collapse progresses.

The authors observe that (again, playing along with their argumentation) there is no big bang. The opposing force supplied by the lower structure is a relatively continuous function (to the inadequate level of resolution present in their data, but again, play along). And this, they say, invalidates Bazant & Zhou's model, and thus their paper is wrong, collapse shouldn't have happened at all, 9/11 Was an Inside Jerb.

This is wrong. This is, in fact, undifferentiated zebra puke.

Bazant & Zhou do not require a "Big Jerk." Their model, as anyone who comprehends their paper knows, is about energy and momentum. These are aggregate quantities -- energy is force times distance, i.e. the force is integrated over a period of motion. So if there's a "Big Jerk" or not, so long as the total energy absorbtion of the lower structure is accounted for correctly, it will provide the right answer.

The authors of this paper, however, are looking at instantaneous acceleration. They aren't dealing with a quantity that averages out. So they need much more precision, precision that isn't found in Bazant & Zhou's model. It isn't needed for that problem.

So, rather than show "Bazant & Zhou is wrong," they've shown "Bazant & Zhou is a poor model of instantaneous acceleration." Big deal. That's not what we're interested in. We're interested in the collapse.

One could also argue, with equal effectiveness, that the collision between the two blocks was not axial, and therefore Bazant & Zhou is wrong. The collisions are not axial, this is true; there is no reason at all to suspect the columns above just happened to land exactly on the columns below. But, again, this doesn't matter. They model it this way because an axial impact is the best possible case if you want the structure to survive.

What Bazant & Zhou present is an upper bound. They put in all kinds of unlikely assumptions that favor collapse arrest. Axial impact is one of them. A square impact between upper and lower block is another. Mr. Szamboti and Dr. MacQueen are, really, taking issue with one of those assumptions, an assumption that we already knew from Day One was unrealistic.

So, what happens if we put in more realism?

We know the impact was not square. This is because the upper blocks tilted first. The tilt smears out each and every impact.

Suppose each floor was 3.2 meters high. The structures were 64 meters across. So, if I tilt the structure by an angle of θ = sin-1(3.2 / 64) = 2.9 degrees, the bottom edge will be tilted over the height of an entire floor. At this amount of tilt or higher, at every instant, the upper block is in contact with the lower floors at the top, bottom, and everything in between. Were the upper blocks tilted by 2.9 degrees or more? You bet they were.

As a result, we don't expect a "Big Jerk" in the first place. At any given instant, the upper block is failing columns gradually. There will be some that are just coming into contact, some that are reaching their buckling point, and some that have completely failed. There is no "Big Jerk" but a steady loading and failing of individual elements. As a result, there's no reason to suspect a sudden change in the structure's resistance. It is a fairly smooth phenomenon.

In fact, Mr. Szamboti and Dr. MacQueen's observation is evidence in favor of a gravity-driven collapse. Think about it. They say there's no "Big Jerk." I agree with them. What this means is that the lower structure, in addition to being hit with an enormous force, was hit asymmetrically. Had there been a "Big Jerk," that would mean the structure, across its entire breadth, was resisting at once, rather than being hit piecemeal, one row of columns at a time. The square impact is more likely to survive. The absence of the "Big Jerk" is only further evidence that Bazant & Zhou overestimated the structure's strength with their model, and therefore the collapse is even less in doubt than it was.

QED.

This is just another black eye for Dr. Jones and his ridiculous self-promotion. One would have to be deeply non-technical to even consider this argument plausible.

- NASA Scientist Ryan Mackey
Entire quote here




[edit on 31-1-2009 by CameronFox]

Architect Dave Rogers also disagrees with the paper:

The actual velocity calculation done in the paper is rather bizarre, and mathematically invalid. The authors are calculating the acceleration required to reach each point in the elapsed time, assuming constant acceleration, and from that deriving the velocity at that point relative to the velocity at the previous point. What they are therefore calculating is not the true velocity; in effect, they're applying a smoothing algorithm based on averaging all the previous points. Looking at their results in rather more detail, it turns out that the reason for this is that they are measuring movements of small numbers of pixels, so a velocity graph obtained by numerical differentiation - which would give a correct velocity - would show pronounced steps in the velocity. This in itself invalidates the entire analysis. The authors are taking a dataset which consists of discontinuous steps in velocity, applying a smoothing algorithm so as to produce a continuous function, then pointing out that the first derivative of this function contains no discontinuities.

Quite simply, the resolution of the data is insufficient to carry out the analysis, and the attempt to rectify this by effectively smoothing the data renders the conclusion invalid. I'll be charitable and describe this as lack of understanding of data resolution and experimental error issues by the authors, rather than deliberate intent.

Dave Rogers


I will post his more detailed explanation for those that are interested.

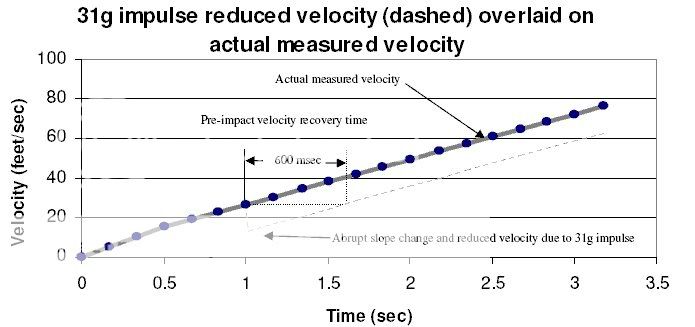
I commented in post #24 that the analysis technique used in the paper is effectively smoothing the data, then commenting on the fact that no discontinuities can be observed in the smoothed data. I thought a little more analysis might be in order, to demonstrate just how serious a fault this is. McQueen and Szamboti claim that the effect they are looking for, which may be summarised as a 13.13ft/sec decrease in velocity at one second into the fall, should be seen as a step in the velocity graph, and represent this as the dotted line in their figure 4, reproduced below [1]. This dotted line is not backed up by any calculations, simply asserted as fact.

To determine the actual appearance of an abrupt 13.13ft/sec decrease in velocity at 1 second elapsed time, I set up an Excel spreadsheet using the time points from McQueen and Szamboti's paper. I then calculated velocities and hence displacements downward for the following scenario:

1. Upper block falls at 1G acceleration for one second.
2. Upper block then experiences an abrupt reduction in velocity by 13.13ft/sec.
3. Upper block then continues to accelerate downwards at 1G.

This closely reproduces the scenario that McQueen and Szamboti claim will produce a large negative step in their analysed data.

Using this dataset, I then reproduced the expected measurements by rounding each displacement point to a multiple of 0.88 feet, corresponding to the pixel spacing calculated in the paper. The resulting dataset was then analysed using the methodology outlined in the paper. Results are shown below in a table, and the calculated velocity is plotted as a graph against time.

The result is that, despite the presence of an abrupt deceleration in the original data, no step discontinuity can be seen in the calculated velocity, in contradiction to the assertion in the paper. This is, as I previously commented, a consequence of the methodology used for analysis, which effectively applies a smoothing function to the data.

The conclusion of the paper is therefore comprehensively refuted. The analysis methodology used by the authors renders it impossible to detect any abrupt change in velocity. Their failure to do so is therefore unrelated in any way to their starting data.

Dave Rogers

I hope I didn't jump the gun too quick. I believe the OP posted an "updated" paper. The original paper released by Journal of 911 Studies was released back on or around the 15th of January. Apparently, after they were contacted by a few people, their "peer review" paper was somewhat revised with corrections.

Originally posted by hgfbob

"It is also important to note here that Bazant was off by a factor of ten in his calculation of the stiffness of the columns, with his 71 GN/m estimate. [8] The actual stiffness, calculated here using the actual column cross sections, is approximately 7.1 GN/m. (see Appendices B and C)
[

If this is true, then they just rendered their whole video analysis useless.

They should have corrected his data, then look for a jolt that corresponds to THAT instead.

Originally posted by CameronFox
I hope I didn't jump the gun too quick. I believe the OP posted an "updated" paper. The original paper released by Journal of 911 Studies was released back on or around the 15th of January. Apparently, after they were contacted by a few people, their "peer review" paper was somewhat revised with corrections.

Kinda questions the value of their peers then, eh?

Anyways, the thing that will escape the TM is that this is a best case scenario that skews the scenario in every way for halting the collapse, and assumes that the buckling columns will come down and hit the lower columns squarely and not slide off, etc.

Clearly, this didn't happen, nor could it ever happen.

The true scenario is that the columns missed each other, and the descending columns/upper block would have hit the floors instead. Even if we again skew this scenario into the unreal and say that the upper block descended squarely, the floors couldn't hold the weight without either breaking from their mounts or just coming apart as the columns punched through. Again, even if you skew the scenario into the unreal and gently place the columns on the floors, and forget any KE, they'll fail. And if we skew it even further and say that the columns buckled exactly in the middle, and the descending columns contact the lower floors at the same time as the lower columns contact the descending floors, the result is the same. They fail.

As a side note, it is important to remember that as these floors fail, columns become unbraced, and more susceptible to buckling and/or breaking at the welds. This becomes important to collapse progression.

So the collapse progresses. the columns hit the next floor, and the scenario is the same - they fail. After several floors fail, the above mentioned columns have no become unbraced over 30-40' and would buckle/break at the welds, and add to the descending mass in the case of the core columns. The ext columns would presumably be pitched over the side and probably not add much to the descending mass.

All this is so simple, that it is no wonder why NIST didn't bother to do any analysis of it.

the results are self evident.

reply to post by Seymour Butz


They were ignoring the folks that were pointing out their errors. (two of them truthers)

Yeah, great peer review process huh?

I find it so sad that those members here that actually know what a crock this article is don't step in to try and educate the TM.

The biggest screwup in this article, IMHO, is how a structure that they state has a FOS of 3, can supply a 31g jolt to the descending upper block.

So the opportunity to educate is lost.

So sad....

Originally posted by Seymour Butz

Originally posted by hgfbob

"It is also important to note here that Bazant was off by a factor of ten in his calculation of the stiffness of the columns, with his 71 GN/m estimate. [8] The actual stiffness, calculated here using the actual column cross sections, is approximately 7.1 GN/m. (see Appendices B and C)
[

If this is true, then they just rendered their whole video analysis useless.

They should have corrected his data, then look for a jolt that corresponds to THAT instead.

they did, if you would have read the paper, you would have known that

and the 31g jolt to the descending upper block, is from Bazants paper

Originally posted by hgfbob

they did, if you would have read the paper, you would have known that

and the 31g jolt to the descending upper block, is from Bazants paper

So they looked for a 31g jolt, that they say is wrong because the columns aren't that stiff. So according to this, the "jolt" should have been less, right?

Bazant says that the lower structure would have been overloaded by 31x. He does not say that the UPPER structure would have seen a 31g jolt. Your peeps made that up.

I dare you to find the part where he says what you claim, or admit that due to intellectual bankruptcy, you are repeating the lies that you read without understanding them.

The paper in question can be found here: www.911-strike.com...

Do you agree with what I wrote a couple of posts back, where i stated that this is just an engineering exercise, and halting the collapse REALLY depends on the FLOORS halting the collapse?

Still so sad that no SE's in the TM have decided to come to this thread and explain to others in the TM exactly WHY this paper is junk.

I think this speaks volumes.

The TM thrives on speculation, and not on facts.

Originally posted by Seymour Butz
Anyways, the thing that will escape the TM is that this is a best case scenario that skews the scenario in every way for halting the collapse, and assumes that the buckling columns will come down and hit the lower columns squarely and not slide off, etc.

I've held off on commenting on Mackey's post because if that were actually posted on ATS, it would have been removed because of it's crudeness.

One must be so full of themselves to talk as such.

Anyway, moving on.

Mackey says that a full-on axial collapse is the best case scenario for building sustainability. How is this possible?

One could also argue, with equal effectiveness, that the collision between the two blocks was not axial, and therefore Bazant & Zhou is wrong. The collisions are not axial, this is true; there is no reason at all to suspect the columns above just happened to land exactly on the columns below. But, again, this doesn't matter. They model it this way because an axial impact is the best possible case if you want the structure to survive.

If the columns did not collide axially, then the columns below would be able to punch through the floor pans above the same as they want us to believe that the columns from above would punch through the floor pans below. Equal and opposite reactions and all.

I'll leave it at that. Like others who are nothing but crude, Mackey is not worth my time.

The true scenario is that the columns missed each other, and the descending columns/upper block would have hit the floors instead.

And the columns below would have hit the upper floors. What do you think happens then? That the columns still would loose and buckle?

Originally posted by Seymour Butz
And if we skew it even further and say that the columns buckled exactly in the middle, and the descending columns contact the lower floors at the same time as the lower columns contact the descending floors, the result is the same. They fail.

How can the lower (stronger) columns fail against the floors that have the same strength as the floors below when the columns above (weaker) are able to destroy the floors below that have the same strength as above?

All this is so simple, that it is no wonder why NIST didn't bother to do any analysis of it.

the results are self evident.

Yes, like magic bullets.

Originally posted by Seymour Butz
Do you agree with what I wrote a couple of posts back, where i stated that this is just an engineering exercise, and halting the collapse REALLY depends on the FLOORS halting the collapse?

Do you agree that the lower columns would have punched through the upper floors the same?

Originally posted by Griff

And the columns below would have hit the upper floors. What do you think happens then? That the columns still would loose and buckle?

I agree with everything you said, other than the unnecessary character assassaination.

Yes, BOTH would be happening at the same time. Floors on both the descending upper block would fail, as would the lower floors when the columns descended onto them. Even if you gently placed them thus, it wouldn't change that, for the weight would be concentrated on the column ends. We'll ignore the fact that offsetting the upper block would mean that some ext columns would be "hanging" ouside the lower block.

Anyways, those floors would fail or be punched through, then on to the next set - upper and lower - floors. they would fail also. After a few floor failures, the columns would be unbraced over a considerable length, and prone to buckle at that point.

Originally posted by Griff

How can the lower (stronger) columns fail against the floors that have the same strength as the floors below when the columns above (weaker) are able to destroy the floors below that have the same strength as above?

The descending columns would either punch through the floors, since the weight is concentrated on the column ends, or if they happened to come down/up on a floor connection, the floor connections couldn't be expected to hold the weight of the upper block.

So the floors would be compromised, leaving the columns unbraced to some degree.

And since the collapse was at an angle, the now minimally/unbraced columns would buckle and/or break welds.

So it wouldn't happen immediately, but after a few floor's worth of drop.