Dividing by zero

Not that it will help, because no one wants to hear what real scientists have to say, but the above poster is correct when he says black holes have nothing to do with this. Just because someone once mentioned the word infinity with both does not mean it will help you understand the problem here.

The "problem" with the back hole singularity is not that there's an "infinity," but that a theorem on existence and uniqueness of solutions to certain kinds of partial differential equations fails due to one of its assumptions no longer being satisfied, causing the initial value problem for trajectories intersecting the singularity to be not well-defined. In normal GR, this is okay, because once you hit the singularity you do not come out. It does indicate that the solution is not complete--the complete equations would be well-posed. But this is only an issue to worry about when you want to understand the quantum mechanics of black holes. Nothing to do with dividing by zero.

reply to post by yampa


How do you explain that dividing a number (for example, 5) by 0.00000000000000000000000000000000000000000000000000000000000000000000000000000001 results in a giganormous number? What happens if you keep adding decimal zeroes to the divisor? We're staring the infinity in the face, and that's what makes mathematicians throw their hands up in the air and declare the result undefined.

@Moduli - does the gravitational collapse stop at some point, or does the collapsing body indeed diminish to a point of zero volume? With all the talk about equations and relativity, this question is fairly simple.

Originally posted by wildespace
reply to post by yampa

 

How do you explain that dividing a number (for example, 5) by 0.00000000000000000000000000000000000000000000000000000000000000000000000000000001 results in a giganormous number? What happens if you keep adding decimal zeroes to the divisor? We're staring the infinity in the face, and that's what makes mathematicians throw their hands up in the air and declare the result undefined.

No, it isn't, seriously, does anyone here even bother to think for themselves?

Consider:
5 / -.000001 vs. 5 / .000001
5 / -.00000001 vs. 5 / .00000001
5 / -.0000000001 vs. 5 / .0000000001
5 / -.0000000000000001 vs. 5 / .0000000000000001
etc

Consider this property of basic grade-school arithmetic:
Every real number x different from zero has the property that
there exists another number, denoted 1/x, which satisfies the property:
x * 1/x = 1/x * x = 1.
Zero does not have this property!

etc, etc, etc.

Originally posted by wildespace
@Moduli - does the gravitational collapse stop at some point, or does the collapsing body indeed diminish to a point of zero volume? With all the talk about equations and relativity, this question is fairly simple.

To an external observer, the black hole is the size of its event horizon. An observer who has fallen through the event horizon sees no matter until he slams into the singularity and dies.

No observer ever "sees" a single point which contains all of the mass of the black hole.

Originally posted by Moduli
In normal GR, this is okay, because once you hit the singularity you do not come out. It does indicate that the solution is not complete--the complete equations would be well-posed. But this is only an issue to worry about when you want to understand the quantum mechanics of black holes. Nothing to do with dividing by zero.

The source I cited earlier said it's thought if we had complete well-posed equations, there won't be a singularity. Are you saying there will be a singularity no matter what?

What about the density of the singularity? How can you say that has nothing to do with dividing by zero? If the volume of the singularity is zero, how do you calculate the density without dividing by zero?

Originally posted by Arbitrageur

Originally posted by Moduli
In normal GR, this is okay, because once you hit the singularity you do not come out. It does indicate that the solution is not complete--the complete equations would be well-posed. But this is only an issue to worry about when you want to understand the quantum mechanics of black holes. Nothing to do with dividing by zero.

The source I cited earlier said it's thought if we had complete well-posed equations, there won't be a singularity. Are you saying there will be a singularity no matter what?

What about the density of the singularity? How can you say that has nothing to do with dividing by zero? If the volume of the singularity is zero, how do you calculate the density without dividing by zero?

A singularity is a result of rotations across the axes. It's a purely mathematical artifact. It is also completely dependent on whether you are doing discrete, finite, numerical calculations or mathematically masturbating over infinitesimals. In either case, nothing about the complexities of physical reality are encoded over the simple unit period defined by the number line (including complex intersections).

These people would have rather have you spend your life talking about infinitesimals, infinities and singularities than understand the real structure of the field of numbers and real physics.

Originally posted by yampa
These people would have rather have you spend your life talking about infinitesimals, infinities and singularities than understand the real structure of the field of numbers and real physics.

You speak of real physics.

Do we know the real physics of a black hole singularity without a theory of quantum gravity? Apparently not, and that's part of the problem, which gives us mass divided by a volume of zero in a density calculation for the singularity.

We do have lots of real physics with relativity and quantum mechanics, but since we haven't yet figured out the correct way to make those models compatible, there are gaps between those models, and the black hole singularity apparently falls in one of those gaps.

reply to post by Moduli


I dont think you understood his point.


5 / 0.0001

is a bigger number then 5 / 0.01 ... right?

So that would mean taking a number and dividing it by a number, results in an increasingly larger number, the closer one gets to 0.

so the more 0's you add to, 5/ 0.00001 .... 5/ 0.0000000001 the bigger a number you will get. So is part of this problem you cant say 0.infinite 0's 1 .. because there needs to be an exact finite amount of numerals before the 1 at the end? Basically asking what is the smallest divisible number before 0 is reached, and what is the nature of that fence between that number and 0. And how come smaller numbers yield larger results when divided by, wouldn't 0 yield the largest?

Originally posted by Arbitrageur

Originally posted by yampa
These people would have rather have you spend your life talking about infinitesimals, infinities and singularities than understand the real structure of the field of numbers and real physics.

You speak of real physics.

Do we know the real physics of a black hole singularity without a theory of quantum gravity? Apparently not, and that's part of the problem, which gives us mass divided by a volume of zero in a density calculation for the singularity.

We do have lots of real physics with relativity and quantum mechanics, but since we haven't yet figured out the correct way to make those models compatible, there are gaps between those models, and the black hole singularity apparently falls in one of those gaps.

Which still has absolutely nothing to do with the number line or observed data.

reply to post by ImaFungi

No, I think he understands it very well. What a few here seem to miss is, that you only get larger numbers (approaching infinity) with a positive divisor. With a negative divisor you will get smaller numbers (approaching negative infinity).

Just have a look at the function 1/x

The are ways to work with this by mapping negative infinity onto positive (Riemann sphere). But you'll still have this issues: Infinity cannot be added to itself, and 0/0 is still undefined.

Originally posted by yampa
Which still has absolutely nothing to do with the number line or observed data.

I'm usually the one arguing about the importance of observed data, so you have a point there.

However the topic of this thread is dividing by zero. The number line you drew doesn't exactly match the topic, because it shows zero itself, but not dividing by zero.

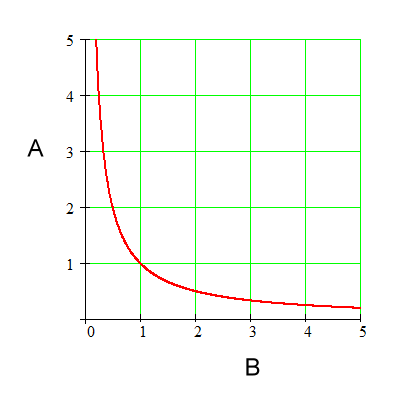
If you want to see what dividing by zero looks like plotted on a number line, here is an example:



As B approaches zero, the plot approaches infinity (A=1/B). So, it's not really possible to show dividing by zero precisely in this fashion, though we can imagine the limit of where the red line goes as B approaches zero, and try to visualize it that way. You can also reflect this graph for negative numbers. This isn't quite the same picture you painted with your number line here:

Originally posted by yampa
Zero makes a lot more sense when you put in the axes. The number line is positional, each space takes a unit, zero allows you to use all 10 positions from the decimal system etc. It allows you to use the same set of numbers for negative and positive on the same line.

In some ways it seems like you're trying to change the topic of the thread from dividing by zero, to just zero. It's not exactly the same topic, though zero itself is also an interesting topic, as the Greeks didn't even have a symbol for zero, etc. But I think that could be a separate thread.

After a little bit of further thought I understand why dividing by 0 does not yield infinity, and is termed undefined.

6/3 is asking, 3 groups of what number will give you 6? The answer is 3 groups of the number 2 will give you 6.

6/0 is asking, 0 groups of what number will give you 6? There is no answer because it is an illogical question. You cant arrive at the positive number 6, with 0 groups of any number. So the answer cant be 0, 0 groups of 0 is 0. cant be 1, 0 groups of 1 is not 6. etc. So it is unanswerable and unaskable.

reply to post by Arbitrageur


That is not a graph of dividing anything by zero. None of the points on that graph would be met by dividing anything by zero. You are pretending to envision an infinitesimal, but as you say, that is never actually calculated (or even attempted, numerically).

And none of this says anything to do with physical reality. And none of this has anything to do with black holes.

Just don't do it. I am kind of math inclined and am okay with 1/0=oo(infinity)...or as you approach 0, the solution approaches infinity.

Originally posted by wildespace
There are two things that show this (at least the two that I'm aware of):

1. Black holes. Density = mass / volume. The singularity at the centre of a black hole is an infinitely small point with infinite density. For a black hole, the formula is density = mass / 0 and the result is infinity.

2. Divide a number by a divisor that is 0, for example 0.5 ... Note the result. Then decrease the divisor by half (to 0.25) and note what happens to the result. Keep halving the divisor, and you'll see that as it approachers zero, the result approaches infinity.

For me, the two examples are quite enough to conclude that dividing by zero results in infinity.

Point 1 shows the flaws of our current physical models rather than adding support to any other hypothesis. A quick fix for this would be to alter gravity to become repulsive below the Schwartzchild radius, effectively distributing the mass around the event horizon which must always have a > 0 surface area and therefore volume.

Point 2 is logical but X / 0 = Infinity isn't right because that would lead to 0 * Infinity = X. Logically I think X / 0 = Undefined is the correct answer

Maybe the universe is a physical representation of 1/0. Starting with 1 whole, and trying to make it equal 0. Infinitesimally dividing 1. Kind of the idea of entropy. And how would that relate to 1/infinity?

Also I have heard there are different types of infinity, so is it wrong to use the word infinity in math? For the math inclined, can It be true that Infinity ≠ Infinity... In which case it would be possible for Infinity > then Infinity x Infinity?

Or is there one supreme = infinity, and then everything else is conditionally infinite, as in a specific irrational number with the potential to infinitely compute its irrational fraction?

Originally posted by yampa
I have no interest at all in listening to Michio Kaku. He is basically a propagandist.

For whom?

Black holes are completely tenuous, totally abstract mathematical theories. They have nothing to say about the simple and natural division of the number line.

The reality is exactly the opposite. Black holes are physical real things.

The number line is a totally abstract mathematical construction.

And totally abstract human mathematicians have worked out the problems with infinities and their various types in the late 19th century.

Originally posted by mbkennel

Originally posted by yampa
I have no interest at all in listening to Michio Kaku. He is basically a propagandist.

For whom?

Black holes are completely tenuous, totally abstract mathematical theories. They have nothing to say about the simple and natural division of the number line.

The reality is exactly the opposite. Black holes are physical real things.

The number line is a totally abstract mathematical construction.

And totally abstract human mathematicians have worked out the problems with infinities and their various types in the late 19th century.

edit on 31-8-2013 by mbkennel because: (no reason given)

Err, no, the natural structure of numbers is not created by humans. It is only rediscovered. And if you calculate something, as in, actually run the numbers - then that ties you to using non infinitesimal methods (name me an algorithm, counting machine or numerical calculation which computes over infinites).

Black holes were created as purely mathematical constructs. Then they went out and tried to fit data to their speculation. Maybe there are physical phenomena which match that model, maybe there aren't. It's unknown, and certainly not physically concluded in any way (but you wouldn't guess that by the way popular science outlets phrase their articles and insert misleading photos).

What is known is that the basis for the original black hole speculation is a complete hack. It's a hack which sources from misunderstandings of Relativity. Einstein knew that, that's why he knew the idea was silly. Not silly because massive gravity wells cannot possibly exist, silly because the models sourced from a poor understanding of mathematical theories. The absurd romancing of singularities is one of the primary causes of this.

Michio Kaku works for himself, PR and western industrialism. People on this forum generally know to be distrustful of the types of truth which emanate that type of person - it's just that people haven't caught on to the reality that occupational lying has infected modern science as badly as it's infected everything else.

reply to post by yampa


If not a black hole, what exists at the center of the galaxy?

What is your understanding of the term black hole and what it physically means?

I don't think a black hole represents zero or infinity. So far as I could presume or calculate, black hole mass still conserves mass. I think it's just that the mass that is co-located becomes so large that the normal separation between the nucleus and electrons starts to become really compressed, if not on top of each other altogether. When the size of the mass becomes that large, then the bending of light due to gravity sucks it in and doesn't allow it out, hence 'black hole'.