It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
18
share:
Analysis of the Cecconi silver photograph
by Antoine Cousyn (myself) and Francois Louange
This thread is the continuation of this one: An in-depth review of the Cecconi Case Photos were I begun to be interested in the case and to search for the original unmodified photo.
It tooks me more than two months efforts to finally succeed in finding the original B&W 6x6 plate, with the help of E. Russo from the Italian CISU. (Many thanks to him BTW)
Here's the original scanned photography, resized (640x480) to fit within the forum screen:

Photographic parameters
• Picture taken on June 18th 1979, above the Treviso airport (Italy), with a Vinten F-95 camera
• Film format 70x70 mm
• Unknown focal length, with 4 possible preset values: 76 mm, 100 mm, 152 mm or 300 mm.

Geometric parameters

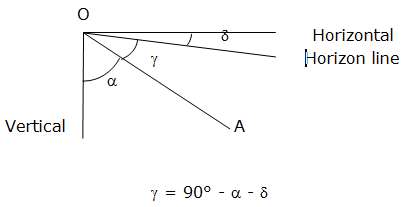
Consider the following points:
O : camera’s lens
H : vertical projection of O on the ground
A et B : extremities of a known parcel on the ground
B’ : projection of point A on OB
Assuming points H, A and B are aligned (approximately), we have the following sketch in the vertical plane that contains H, A and B:
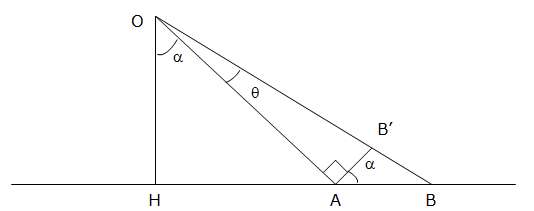
• Known flying altitude:
OH = 7000 ft = 2134 m
• Known length of the AB parcel spotted on the ground:
AB = 381 m
• Unknown alpha angle between the OH vertical and the OA line
Attempt to determine the focal length
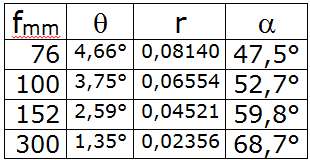
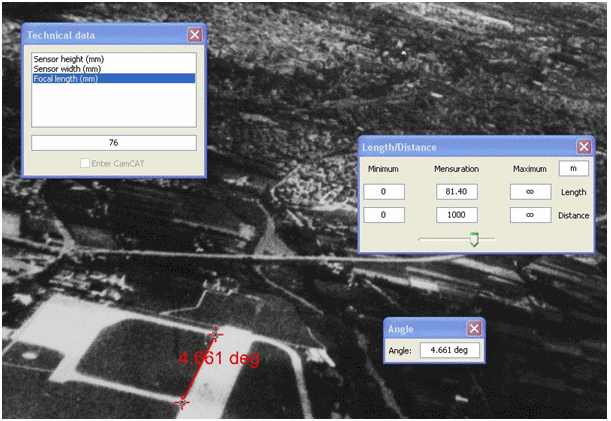
After inputting the film’s dimensions (70 mm x 70 mm) and the focal length (76 mm, 100 mm, 152 mm or 300 mm) into the Camera menu of our favorite analysis software, one may measure the alpha angle and infer the value of the r ratio, thanks to the Length/Distance function:
r = AB’ / OA
Knowing that:
AB’ = AB cos alpha
OA = OH / cos alpha
One infers:
r = (AB / OH) cos2 alpha
Thus:
alpha = arccos alpha (r / 0,17857)
Measurements with our favorite analysis software (see diagram below) give the following results:
In order to determine the most probable value for the focal length, we shall make use of the horizon line, visible on the picture.
Let us compute first the angle value between the line of sight towards the horizon and the horizontal from the camera, which is at an altitude of 7000 feet (2134 m).
The following sketch shows the Earth, with its R radius, the previously defined points O, H and A, the horizon line and the horizontal passing through O.
The wanted angle is delta:
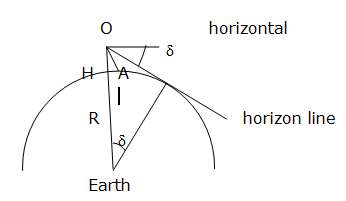
Knowing the values of the altitude OH = h'c' and of the Earth’s radius R:
h'c' = 2134 m
R = 6371000 m
One computes:
Delta = arccos [R / (R + hc)]
Delta = 1,5 °
The angle gamma between the camera’s line of sight towards point A and the camera’s line of sight towards horizon is inferred from alpha, previously estimated for each of the possible focal lengths, and from the delta angle:
For each possible value of the focal length, we shall measure gamma with the Angle function of our favorite analysis software, and compare the result to that given by application of the previous formula.

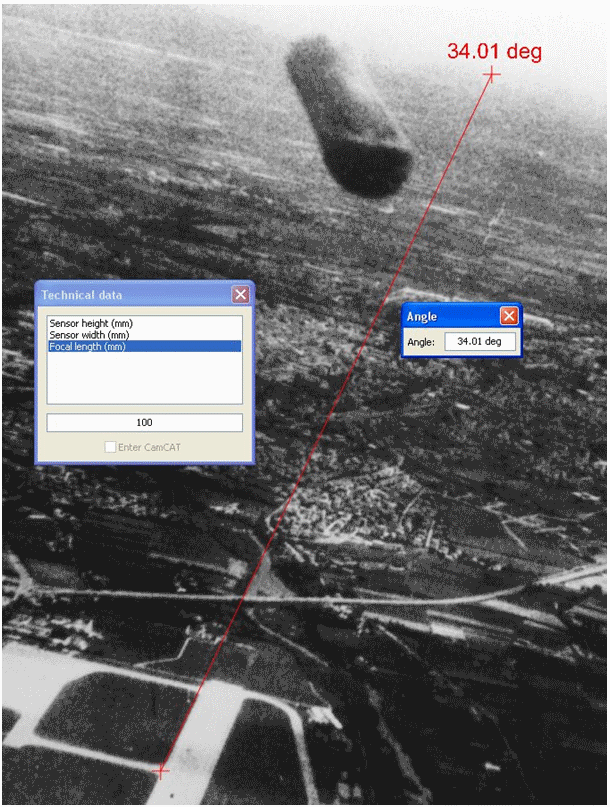
Measurement for f = 100 mm
The most coherent result, expressed by a minimum difference in absolute value (taking into account simplifications in computations and uncertainties in measurements), corresponds to:
f = 100 mm
It should be noted that values of « gamma computed» and of « difference », indicated in the table above, increase or decrease if the flying altitude increases or decreases as compared to 7000 feet. More precisely, calculation shows that the “difference” would be null if we assumed:
f = 76 mm and h = 7800 ft
OR
f = 100 mm and h = 6400 ft
Without finally discarding the value of 76 mm, for which coherence is not very significantly worse, we shall therefore retain the value of 100 mm for the following study, bearing in mind that the residual uncertainty will not call into question the orders of magnitude which will be evaluated.
Study of the unidentified object
The object appears approximately in the form of a “cigar” (cylinder), the nearest extremity of which is dark. Flying at an altitude slightly lower than that of the plane, it is lighted from above, which is compatible with natural lighting by the sun, and its main axis is parallel to the ground.
The angular measurement of its diameter gives:
3,473 °

To this angular size corresponds a ratio between the diameter of the object and its distance d from the camera:

Attempt to estimate the distance from the unidentified object
If the nearest extremity of the object is really black or very dark, comparison of its apparent luminance with that of the darkest elements of the ground should provide information on the ratio between camera-to-object and camera-to-ground distances, taking into consideration atmospheric diffusion.
The following illustration displays the measurement of the darkest pixel, respectively in 3 strips of the image and at the dark extremity of the object.

It appears that dark points on the ground are far darker than the object. This would imply, if the object was really black, that it would be farther away than the ground in the strips, i.e. farther than 10000 feet.
If it had been 10000 feet away from the camera, the object would have had a diameter in the order of 200 m. On the other hand, the value of its h'ufo' altitude would have been inferred from the h'c' value of the camera’s altitude through the following simplified formula:
h'ufo' = h'c' – d sin ( phi + gamma)
where gamma is the above-defined angle and phi the angle between the camera’s line of sight towards the object and the camera’s line of sight towards the horizon line.

h'ufo' = 7000 – 10000 sin (5,49 + 1,5)
h'ufo' = 5800 ft
Now, an object with a 200 m diameter, flying at an altitude of 5800 ft (1800 m), could certainly not have gone unnoticed from the ground, in particular in an urban area and on a relatively clear day.
This only proves that the original assumption was wrong: the object was not completely dark, and therefore could be at any distance from the camera (less than 1000 ft).
edit on 20-10-2012 by elevenaugust because: typo
edit on 20-10-2012 by elevenaugust because: (no reason
given)
edit on 20-10-2012 by elevenaugust because: (no reason given)
extra DIV Conceivable explanations
The type of known object which is most comparable to the cigar-shaped object displayed on the photograph is a balloon: either an airship, or a toy “solar airship”.
Airship
Modern airships, produced by around 15 manufacturers around the world (Airship Industries, Zeppelin , Goodyear, Huajiao Airship, Voliris, WDL, etc.) have diameters ranging from 8 m to 16 m, the value of 14 m appearing to be the most common one. They can fly at altitudes far higher than 7000 ft.
Under that hypothesis, estimated distance between airship and plane:
For a diameter of 8 m: 130 m
For a diameter of 14 m: 230 m
For a diameter of 16 m: 260 m
However, the general aspect of the picture, the impression of the object’s closeness, and - above all - the object’s irregular shape, do not really suggest a commercial or military airship.
Toy solar airship
This type of toy has been popularized in France by the Pif Gadget fanzine (special issues in July 1981 and June 1982), but it already existed before in several countries, in particular in Germany, with the similar YPS fanzine (YPS n° 450 and Yps-Extra n°3 in May 1980: the Solarzeppelin triggered then a wave of UFO reports), Pif in Spain and Romania, as well as others in other countries.
The solar balloon, or “solar UFO”, appears as a cylinder with a length from 2 to 3 m and a diameter from 60 cm to 2 m, 1 m being the most current value. Certain models are supposed to fly up to 9000 ft.
Under that hypothesis, estimated distance between balloon and plane:
For a diameter of 60 cm: 10 m
For a diameter of 1 m: 16 m
For a diameter of 2 m: 33 m

The solar balloon hypothesis seems credible, if one considers:
• The object’s aspect
• The object’s color (dark but not black, because reflecting)
• The order of magnitude of the length/diameter ratio
• The closeness between the camera and the object
• The existence of other rather similar testimonies or photographs, sometimes with the established presence of a toy “UFO airship”.
• Examples found on the Internet for the same period (not checked):
- Mestre (Italy), June 1979:
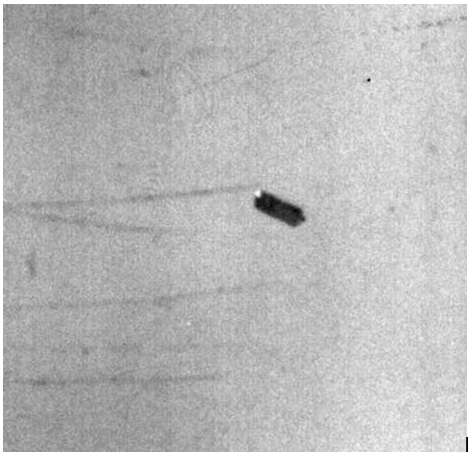
- Hamburg (Germany), July 1980:

It should be mentioned that if the photograph under study effectively displays a balloon of this type, it cannot be a model originating from Pif Gadget, taking into account the publication dates, later than the picture.
(Provisional) conclusion
No formal demonstration could be made, but the most credible rational explanation remains that by a solar airship (toy), which would have been photographed from the plane, at nearly the same altitude, from a distance of around 15 meters.
Thanks for their help in this investigation to:
- My partner François Louange
- Edoardo Russo (CISU)
- Gerald Drape of the German NARCAP and MUFON.
The type of known object which is most comparable to the cigar-shaped object displayed on the photograph is a balloon: either an airship, or a toy “solar airship”.
Airship
Modern airships, produced by around 15 manufacturers around the world (Airship Industries, Zeppelin , Goodyear, Huajiao Airship, Voliris, WDL, etc.) have diameters ranging from 8 m to 16 m, the value of 14 m appearing to be the most common one. They can fly at altitudes far higher than 7000 ft.
Under that hypothesis, estimated distance between airship and plane:
For a diameter of 8 m: 130 m
For a diameter of 14 m: 230 m
For a diameter of 16 m: 260 m
However, the general aspect of the picture, the impression of the object’s closeness, and - above all - the object’s irregular shape, do not really suggest a commercial or military airship.
Toy solar airship
This type of toy has been popularized in France by the Pif Gadget fanzine (special issues in July 1981 and June 1982), but it already existed before in several countries, in particular in Germany, with the similar YPS fanzine (YPS n° 450 and Yps-Extra n°3 in May 1980: the Solarzeppelin triggered then a wave of UFO reports), Pif in Spain and Romania, as well as others in other countries.
The solar balloon, or “solar UFO”, appears as a cylinder with a length from 2 to 3 m and a diameter from 60 cm to 2 m, 1 m being the most current value. Certain models are supposed to fly up to 9000 ft.
Under that hypothesis, estimated distance between balloon and plane:
For a diameter of 60 cm: 10 m
For a diameter of 1 m: 16 m
For a diameter of 2 m: 33 m

The solar balloon hypothesis seems credible, if one considers:
• The object’s aspect
• The object’s color (dark but not black, because reflecting)
• The order of magnitude of the length/diameter ratio
• The closeness between the camera and the object
• The existence of other rather similar testimonies or photographs, sometimes with the established presence of a toy “UFO airship”.
• Examples found on the Internet for the same period (not checked):
- Mestre (Italy), June 1979:

- Hamburg (Germany), July 1980:

It should be mentioned that if the photograph under study effectively displays a balloon of this type, it cannot be a model originating from Pif Gadget, taking into account the publication dates, later than the picture.
(Provisional) conclusion
No formal demonstration could be made, but the most credible rational explanation remains that by a solar airship (toy), which would have been photographed from the plane, at nearly the same altitude, from a distance of around 15 meters.
Thanks for their help in this investigation to:
- My partner François Louange
- Edoardo Russo (CISU)
- Gerald Drape of the German NARCAP and MUFON.
edit on 20-10-2012 by elevenaugust because: (no reason given)
Tonio, you set the bar higher than most can reach. Excellent presentation!
I can't add much more than in the first thread and remain intrigued by the object and mystified as to why the other images weren't released. As much as I want to keep the sense of mystery alive, the probability is high that we're discussing a solar zeppelin-type balloon.
I have one question. Would a solar zeppelin balloon reach that altitude? I've had a quick look and couldn't find a sensible answer.
I also have a point to make and that's the problem of the first claimed explanation. The teacher who claimed responsibility described creating the object from bags which casts doubt on a mass-produced solar zeppelin although not the premise that a cylindrical balloon had been released.
Anyway, I'm just thinking aloud and will go away and re-read the other thread.
I can't add much more than in the first thread and remain intrigued by the object and mystified as to why the other images weren't released. As much as I want to keep the sense of mystery alive, the probability is high that we're discussing a solar zeppelin-type balloon.
I have one question. Would a solar zeppelin balloon reach that altitude? I've had a quick look and couldn't find a sensible answer.
I also have a point to make and that's the problem of the first claimed explanation. The teacher who claimed responsibility described creating the object from bags which casts doubt on a mass-produced solar zeppelin although not the premise that a cylindrical balloon had been released.
Anyway, I'm just thinking aloud and will go away and re-read the other thread.
reply to post by elevenaugust
Well done. Very well done indeed.
Solar balloon does indeed fit the profile.
It wouldn't be too far fetched for a large number of 'cigar' shaped UFO reports also to be such.
Questions that arise with this are time period, material availability, cost, and relative weight of material available at the time period.
Were there sufficiently light weight/thin and readily available plastics as common today in 1979?
Contemporary plastics of extremely thin/light-weight and low cost are common now. Then?
Other materials possible for use?
Well done. Very well done indeed.
Solar balloon does indeed fit the profile.
It wouldn't be too far fetched for a large number of 'cigar' shaped UFO reports also to be such.
Questions that arise with this are time period, material availability, cost, and relative weight of material available at the time period.
Were there sufficiently light weight/thin and readily available plastics as common today in 1979?
Contemporary plastics of extremely thin/light-weight and low cost are common now. Then?
Other materials possible for use?
edit on 20-10-2012 by Druscilla because: (no reason given)
Just wanted to say great work, obviously must have taken some time and really worthwhile.
The object in the photo appears to be pretty parallel to the ground whereas all of the pics I have seen of solar balloons of this shape show them to be tipped, with one end pointing more to the ground. Course you could argue gust of wind etc and the end facing the camera does look as if it could be partially deflated.
The object in the photo appears to be pretty parallel to the ground whereas all of the pics I have seen of solar balloons of this shape show them to be tipped, with one end pointing more to the ground. Course you could argue gust of wind etc and the end facing the camera does look as if it could be partially deflated.
That image is most-definitely of a solar balloon. No doubt about it.
IN the top area of the object,noticed a hump and by the close end is flat.......i see the solar balloons are in round shape......just my 2.
reply to post by elevenaugust
Thank you for a great image analysis... and a rather reductionistic conclusion.
I encourage everyone to visit the first part/thread of this image anlysis, where you can find additional source material:
www.abovetopsecret.com...
I do so because if you do study the case in-depth, the OP's conclusion doesn't really seem realistic.
Take for instance the UFOcasebook article on the subject and read it with care:
www.ufocasebook.com...
Here are some things that caught my attention:
the pilot ... approached the UFO up to a distance of 70-80 meters and at speeds estimated at 300 knots (450-500 km.
It is my personal opinion that such an approach would create enough airstreams to send a balloon (solar-zeppelin) flying in all different directions, in any case I believe it to be enough for an experienced pilot to identify a free-flying, lighter-than-air obect for what it is. It become even stranger when we read that :
Cecconi made seven to eight passes close to the object and each time took gun camera film of the UFO...
So, eight passes wasn't enough for Cecconi to identify "a balloon" as a balloon. Perhaps it has something to do with the fact that the object didn't behave as a balloon.
The apparent UFO was stationary relative to the G-91, but the radar center confirms to Cecconi that it was moving, course and speed defined... He was in close pursuit at 7,000 feet altitude but did not know its wake. When the Pilot closed on the object it made up and down movements at 1,000 feet at a time, climbing up to 13,000 feet.
We have radar confirmation on this.
The airport ground staff followed the scene with binoculars. The Treviso Control Tower personnel called Cecconi to warn him that the object was discharging a strange "blue trail."
The airport ground staff weren't able to identify the 'balloon' as a balloon either, even though they are - as pilots - trained to identify any type of flying objects. And what about the "strange blue trail"? All in their imagination I suppose, a collective hallucination no doubt...
The witness recalled a "gas tank" of matte black and the presence of a small white or clear "dome," located on the upper side, of the slightly flattened object.
This is not apparent in the photograph, so in that context the image analysis does not need to take it into consideration. But if we're going to give any credence to the main witness - a trained and experienced pilot - shouldn't we at least take his observations into account? After all, radar and ground witness observations confirm his report.
The "dome" was like a kind of shaped like those found on sports cars. While Cecconi was making yet another tack to get back to doing another round of photographs, Istrana radar called to report the object suddenly disappeared from theirs and other radars.
After a few seconds, the Treviso control tower confirmed the UFO had visually disappeared. A few minutes later, the plane landed and the films were removed and quickly developed.
The natural debunker explanation to this must be that the solar airship broke and fell to the ground. But none of the parties observing the object were apparently able to see this, and no solar-zeppelin was ever found to my knowledge.
So, I conclude that in order to reach the conclusion that this was but a solar-zeppelin, all you need to do is to ignore that:
The object did not behave like a balloon.
None of the involved parties were able to identify it as a balloon.
The object did not have the same characteristics as the mentioned solar-zeppelin in the sense that the object was described as "matte black" (which the photograph shows), while the solar zeppelins shown on picture are clearly glossy. Neither does it have a dome.
The trick here is to ignore the accounts of trained air and ground personnel plus radar reports and reduce the whole case to a simple image analysis, well done but misleading if you actually pretend to understand the case as a whole and what this object really was.
So you're suggesting that the pilot risked his life - in spite of air regulations and his own report - by flying as close to the object as 15 meters? You're whole reasoning depends on this totally illogic assumption.
Yeah right, no doubt whatsoever.
Thank you for a great image analysis... and a rather reductionistic conclusion.
I encourage everyone to visit the first part/thread of this image anlysis, where you can find additional source material:
www.abovetopsecret.com...
I do so because if you do study the case in-depth, the OP's conclusion doesn't really seem realistic.
Take for instance the UFOcasebook article on the subject and read it with care:
www.ufocasebook.com...
Here are some things that caught my attention:
the pilot ... approached the UFO up to a distance of 70-80 meters and at speeds estimated at 300 knots (450-500 km.
It is my personal opinion that such an approach would create enough airstreams to send a balloon (solar-zeppelin) flying in all different directions, in any case I believe it to be enough for an experienced pilot to identify a free-flying, lighter-than-air obect for what it is. It become even stranger when we read that :
Cecconi made seven to eight passes close to the object and each time took gun camera film of the UFO...
So, eight passes wasn't enough for Cecconi to identify "a balloon" as a balloon. Perhaps it has something to do with the fact that the object didn't behave as a balloon.
The apparent UFO was stationary relative to the G-91, but the radar center confirms to Cecconi that it was moving, course and speed defined... He was in close pursuit at 7,000 feet altitude but did not know its wake. When the Pilot closed on the object it made up and down movements at 1,000 feet at a time, climbing up to 13,000 feet.
We have radar confirmation on this.
The airport ground staff followed the scene with binoculars. The Treviso Control Tower personnel called Cecconi to warn him that the object was discharging a strange "blue trail."
The airport ground staff weren't able to identify the 'balloon' as a balloon either, even though they are - as pilots - trained to identify any type of flying objects. And what about the "strange blue trail"? All in their imagination I suppose, a collective hallucination no doubt...
The witness recalled a "gas tank" of matte black and the presence of a small white or clear "dome," located on the upper side, of the slightly flattened object.
This is not apparent in the photograph, so in that context the image analysis does not need to take it into consideration. But if we're going to give any credence to the main witness - a trained and experienced pilot - shouldn't we at least take his observations into account? After all, radar and ground witness observations confirm his report.
The "dome" was like a kind of shaped like those found on sports cars. While Cecconi was making yet another tack to get back to doing another round of photographs, Istrana radar called to report the object suddenly disappeared from theirs and other radars.
After a few seconds, the Treviso control tower confirmed the UFO had visually disappeared. A few minutes later, the plane landed and the films were removed and quickly developed.
The natural debunker explanation to this must be that the solar airship broke and fell to the ground. But none of the parties observing the object were apparently able to see this, and no solar-zeppelin was ever found to my knowledge.
So, I conclude that in order to reach the conclusion that this was but a solar-zeppelin, all you need to do is to ignore that:
The object did not behave like a balloon.
None of the involved parties were able to identify it as a balloon.
The object did not have the same characteristics as the mentioned solar-zeppelin in the sense that the object was described as "matte black" (which the photograph shows), while the solar zeppelins shown on picture are clearly glossy. Neither does it have a dome.
The trick here is to ignore the accounts of trained air and ground personnel plus radar reports and reduce the whole case to a simple image analysis, well done but misleading if you actually pretend to understand the case as a whole and what this object really was.
Originally posted by elevenaugust
(Provisional) conclusion
No formal demonstration could be made, but the most credible rational explanation remains that by a solar airship (toy), which would have been photographed from the plane, at nearly the same altitude, from a distance of around 15 meters.
So you're suggesting that the pilot risked his life - in spite of air regulations and his own report - by flying as close to the object as 15 meters? You're whole reasoning depends on this totally illogic assumption.
Originally posted by _BoneZ_
That image is most-definitely of a solar balloon. No doubt about it.
Yeah right, no doubt whatsoever.
edit on 20-10-2012 by Heliocentric because: You rice-field maidens! The only things not muddy Are the songs you sing.
reply to post by Heliocentric
Yes, and that's why I said "provisional conclusion", as it's just, as of today, an image analysis.
Of course, to consider it as a full investigation wasn't the purpose here but, your points (that I'm fully aware of), will be taken into account for the following.
Thanks for taking the time to gather all the witnesses informations, it will be useful!
Edit: and I would like to add that the most interesting part will be to compare the image analysis conclusion and all the testimonies 'analysis' conclusion.
Yes, and that's why I said "provisional conclusion", as it's just, as of today, an image analysis.
Of course, to consider it as a full investigation wasn't the purpose here but, your points (that I'm fully aware of), will be taken into account for the following.
Thanks for taking the time to gather all the witnesses informations, it will be useful!
Edit: and I would like to add that the most interesting part will be to compare the image analysis conclusion and all the testimonies 'analysis' conclusion.
edit on 20-10-2012 by elevenaugust because: (no reason given)
reply to post by elevenaugust
It wasn't my intention to jump down your throat, and your analysis is well-made, bravo!
But people must understand that there is more to this case than just the image analysis.
It wasn't my intention to jump down your throat, and your analysis is well-made, bravo!
But people must understand that there is more to this case than just the image analysis.
That is a fantastic picture, I congratulate you on your hard work getting the original. It looks like an object I saw in a video that was taken in my
city. Cigar shaped, silver in color, it is a most astonishing video and this helps complement the video (or vice versa i suppose). Also many people
have reported UFO's of that shape, this is almost undeniable proof. again, fascinating and congratulations.
Postscript
After a review of the testimony from the picture’s author, conducted investigations, availability of complementary data (photographs, radar...), the previously mentioned hypothesis, presented as the most acceptable conventional explanation for the photograph alone, seems unacceptable for the whole file, in particular because of the stability of the object’s attitude throughout the observation, as well as the altitude - far higher than 7000 feet - at which it would have kept being observed.
At this stage, and without access to all available technical data, one may only file the Cecconi case as unexplained (until further notice).
After a review of the testimony from the picture’s author, conducted investigations, availability of complementary data (photographs, radar...), the previously mentioned hypothesis, presented as the most acceptable conventional explanation for the photograph alone, seems unacceptable for the whole file, in particular because of the stability of the object’s attitude throughout the observation, as well as the altitude - far higher than 7000 feet - at which it would have kept being observed.
At this stage, and without access to all available technical data, one may only file the Cecconi case as unexplained (until further notice).
I concur with the OP's evaluation of the case, unexplainable for now.
new topics
-
Proof of Cleptocracy
US Political Madness: 2 hours ago -
Boy Scouts to be renamed next year
Other Current Events: 6 hours ago -
Pfizer agrees to settle over 10,000 Zantac lawsuits after cancer causing substance found in drug
Medical Issues & Conspiracies: 6 hours ago -
Judas Iscariot Slips The Hangman's Noose
Political Issues: 10 hours ago -
Murder Suicide Investigation Still Active 4 months later?
Other Current Events: 10 hours ago
top topics
-
Ooooh...it worked!!
Members: 14 hours ago, 17 flags -
Judas Iscariot Slips The Hangman's Noose
Political Issues: 10 hours ago, 10 flags -
New House GOP Bill To Send Pro Hamas College Law Breakers to Gaza for 6 Months
Social Issues and Civil Unrest: 17 hours ago, 9 flags -
A Shout-out To truthseeker45 Hoot Hoot
General Chit Chat: 12 hours ago, 4 flags -
Pfizer agrees to settle over 10,000 Zantac lawsuits after cancer causing substance found in drug
Medical Issues & Conspiracies: 6 hours ago, 4 flags -
Murder Suicide Investigation Still Active 4 months later?
Other Current Events: 10 hours ago, 3 flags -
Boy Scouts to be renamed next year
Other Current Events: 6 hours ago, 2 flags -
Proof of Cleptocracy
US Political Madness: 2 hours ago, 2 flags
active topics
-
Boy Scouts to be renamed next year
Other Current Events • 35 • : Annee -
Judge Postpones Trump Classified Docs Trial INDEFINITELY
US Political Madness • 144 • : xuenchen -
Chris Cuomo, who pushed vaccine shots on CNN, admits Moderna vaccine destroyed his health
Mainstream News • 64 • : rdambroso -
NASA Black Hole Visualization - Go Beyond the Brink
Space Exploration • 10 • : andy06shake -
Russia police launch major manhunt after troops massacred by comrade in occupied Ukraine
Other Current Events • 23 • : andy06shake -
Breaking--Hamas Accepts New Cease Fire
Middle East Issues • 298 • : AlongCameaSpider -
Proof of Cleptocracy
US Political Madness • 4 • : ADVISOR -
Candidate TRUMP Now Has Crazy Judge JUAN MERCHAN After Him - The Stormy Daniels Hush-Money Case.
Political Conspiracies • 1412 • : Annee -
Pentagon UFO Hunter Reveals What He Knows About Aliens: Nothing
Aliens and UFOs • 10 • : crayzeed -
New House GOP Bill To Send Pro Hamas College Law Breakers to Gaza for 6 Months
Social Issues and Civil Unrest • 89 • : network dude
18
