Serious math question: Why is the diagonal in a rectangle shorter?

This isn't at all the same as calculus because the line is not getting any closer to the answer. It remains 20 cm no matter how many steps are compressed into it.

Also I don't believe that the smallest unit of space is set up like a grid, so it is possible to move in a straight line. The thing is that nothing is perfectly still. All atoms are vibrating, even at absolute zero, so I would say that nothing has ever yet moved in a truly straight line.

Originally posted by PurpleChiten
you'll enjoy this site very much!!

www.khanacademy.org...

I really love the doodles section, entertaining as well as informative!

www.khanacademy.org...



if ya'll don't mind, there's an unofficial election experiment going on for an imaginary office called "Regent", please feel free to click on the link in my signiture to vote for me...just flag the thread to cast your vote, nothing big and complicated... (this is shameless campagining for a fake position...what can I say...)

Also plan to use this when discussing grad classes particularly related to this book: books.google.com...

ya'll may enjoy it.

Love the stuff you can find on the Khan academy web site, great source of knoledge.

Originally posted by Wide-Eyes
If you're talking about intentionally zig-zagging then I gues it's like angles of a triangle always add up 180degrees. Guess that's what Phage meant about Pythagoras.

edit on 3-7-2012 by Wide-Eyes because: (no reason given)

A triangle drawn on the surface of a sphere will not have angles that add up to 180 degrees. Don't get hung up on Euclid.

Originally posted by Wide-Eyes
reply to post by UnixFE

 

Am I missing something here?

Yes.

Say you have a 10x10 square.

If you travel along its sides from one corner to an opposite corner, you would travel 20 units (10 units along one side, then 10 units along the other. However, if you travel in a diagonal line (the red line in the drawing below) between the two opposite corners of that square, your length of travel would be 14.142 units (there are actually more digits to the right of the decimal, but for simplicity, we'll call it 14.142).

This diagonal length can be found using the Pytagoriam Theorum:

a^2 + b^2 = c^2
10^2 + 10^2 = c^2
100 + 100 = c^2
200 = c^2
√200 = c
14.142 = c

The shortest path between the two corners would be this diagonal line measuring 14.142 units:




Now, imagine if that diagonal line wasn't diagonal, but really made up of a zig-zaggy "stepped" line -- say, for example -- of 10 line segments, like a set of steps.


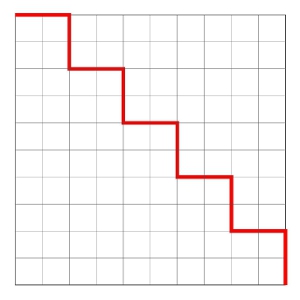
Would the path STILL be shorter? No. if you measure the total distance traveled along the "stepped" path, it would be equal to the length of the path if you traveled along the sides. It you measured along this stepped path, you would see it measures 20 units, which is equal to if you would have simply followed the two sides rather than taking this stepped path



NOW, let's imagine another zig-zag "stepped" line -- but this time the steps in that zig-zag line gets much smaller (and the number of steps more numerous).


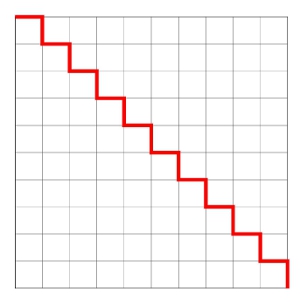
Again, if you measure the total distance traveled along the "stepped" path, it would be equal 20 units -- the same as the length of the path if you traveled along the sides, and the same as the image above with slightly larger steps.


Let's go with even smaller steps:


AGAIN, if you measured the total path along those steps, it will be 20 units



Lets now get finer still:


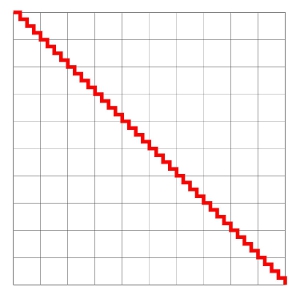
This zig-zag "stepped" path is looking more and more like the straight diagonal line, but again, if you measured the zig-zag path, it would STILL measure 20 units -- while the diagonal measures only 14.142 units


No matter how tiny I make the zig-zags in the stepped line, the total path traveled is still 20 units, rather than 14.142 units along the diagonal. EVEN IF I make those zig-zags so tine that you can only see them with a microscope -- that is to say, so tiny that the zig-zag line actually appears to be diagonal, the path traveled along those infinitesimally tiny zig-zagged steps would still be 20 units, while the "true" diagonal is 14.142 units.

I think the OP is asking "Why?" Why would a line that -- for all intents and purposes LOOKS like a straight diagonal, but is actually made up of thousands or millions of microscopic zig-zag steps -- WHY would that line be 20 units, but the true diagonal be 14.142 units?

The answer lies in calculus.

It's always going to cost you added distance using steps and more energy in some cases.

A diagonal line doesn't have to have a thickness, since all a line is, is 2 points connected.

As long as you have two points you can have an infinitely small line.

By adding steps, you add points, thus more space is required.

Originally posted by IndieA
It's always going to cost you added distance using steps and more energy in some cases.

A diagonal line doesn't have to have a thickness, since all a line is, is 2 points connected.

As long as you have two points you can have an infinitely small line.

By adding steps, you add points, thus more space is required.

I agree, but it seems counter-intuitive that two lines that LOOK exactly the same to the naked eye (one a straight diagonal, and the other the looks diagonal but is made up of millions of microscopic "steps") would be so different in length from a mathematical standpoint.

reply to post by Soylent Green Is People


Think about how much information is needed for a line with millions of steps compared to a line that just has two points.

Originally posted by ImaFungi
reply to post by jiggerj

 

a square is a rectangle,,,


I think he means straight diagonal is shorter then the steps,,,,,, but is wondering why if he shortens the length of each step,, untill they are barely steps,,, but like a jagged wave almost a straight line,,, why its not shorter then the original steps...

edit on 3-7-2012 by ImaFungi because: (no reason given)

i think its because each jagged step,,,, the shorter you make them,,,, the more steps you make,,, and they will still equal the distance,,, because the more kinks the more deviations of straight they are taking,,

edit on 3-7-2012 by ImaFungi because: (no reason given)

Bingo!

reply to post by UnixFE


The tiny zig zig line is not straight whereas your assuming the sides of the rectangle are which is why it is longer. If your arguing that atoms are like little steps and that no line is straight then the two sides of the rectangle can't be straight either, so long as the 'jaggedness' of the sides is equivalent then Pythagorean theorem still holds.

Something we refer to in Graph Theory is the "shortest longest path". I realize it seems a bit oxymoronic, but the shortest distance between the two points is the straight line, but there are other possible paths existant. The shortest of those other possible paths would be the one without any changes in direction making the stairstep model no matter how miniscule.

In application, that straight line is often theoretical but is still the actual diagonal. We only approximate the diagonal in many cases, such as with the stair steps due to physical constraints. As the number of "steps" approach infinity, the staircase would approach the straight line, the theoretical diagonal.

Remember that any time there is a change in direction, another vertex or point is added, thus, it is no longer the distance between two points, but the distance between two points with other points in between them, giving a longer length.


....
....
for some silly "fun stuff:...

We're having a pseudo electional experiment over in BTS for an office that doesn't actually exist... a bit like the "widget" product to theorize the starting of companies...

but anyway, please represent the "NERD VOTE". All you have to do is flag the thread of the 'party candidate' you are supporting (no democrats vs republicans in it at all).

Please take a moment to flag my thread so I can "win" the unofficial, non-existant office

Vote Purple Chiten!

reply to post by 4chi11e

This isn't at all the same as calculus because the line is not getting any closer to the answer.

The line isn't – but the area bounded by the zigzag line and the other two sides more closely approaches the area of the triangle bounded by those two sides as the length of the zigzags approaches zero. That's calculus.

reply to post by UnixFE


Your just replicating the original again but on an increasingly smaller scale.

Pretty cool thought / idea though.

good post.