It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
share:
mumbo jumbo deleted that had nothing to with science or tech but my limited philosophical beliefs that I easily debunk myself the more I think about
it.
edit on 17-2-2019 by InhaleExhale because: (no reason given)
Well, no one replied to my statement, but I stand by my viewpoint, that an actual instance of verifiable infinity does not exist within our
Universe.
I challenge anyone to come up with an example that is actually fully infinite.
There is not.
I challenge anyone to come up with an example that is actually fully infinite.
There is not.
a reply to: Phage
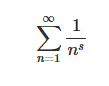
Riemann Zeta Function
If you re-arrange the function using the Euler Product you end up with a function that looks like: 1/(1 - (1/p^s))
[Note: there is more stuff around it but that is not the point]
The graph looks like:

Source: Mathworld.Wolfram.com
The right hand graph shows what happens to the value of the Zeta function as your value of, 1/p^s, approaches 1 from both the negative side and the positive side: the graph shoots towards infinity in either direction.
As a place holder among integers it looks like:
..., -2, -1, "no thing", 1, 2, ...
You can call it Beowulf if you like!
..., -2, -1, Beowulf, 1, 2, 3, 4, ...
Beowulf sits one unit away from -1, and 1. Beowulf sits two units away from -2, and 2. Therefor, Beowulf is an even number.
When used as a functional term like RZ, division by zero leads to infinity. Since that is true for all cases, it is not allowed. All I am saying is, "depends how you are using it [zero], functionally or as a discrete object."
Oddly enough, in the Zeta function, I think it rather elegantly shows that 1 is not a prime number!
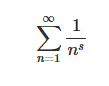
Riemann Zeta Function
If you re-arrange the function using the Euler Product you end up with a function that looks like: 1/(1 - (1/p^s))
[Note: there is more stuff around it but that is not the point]
The graph looks like:

Source: Mathworld.Wolfram.com
The right hand graph shows what happens to the value of the Zeta function as your value of, 1/p^s, approaches 1 from both the negative side and the positive side: the graph shoots towards infinity in either direction.
As a place holder among integers it looks like:
..., -2, -1, "no thing", 1, 2, ...
You can call it Beowulf if you like!
..., -2, -1, Beowulf, 1, 2, 3, 4, ...
Beowulf sits one unit away from -1, and 1. Beowulf sits two units away from -2, and 2. Therefor, Beowulf is an even number.
When used as a functional term like RZ, division by zero leads to infinity. Since that is true for all cases, it is not allowed. All I am saying is, "depends how you are using it [zero], functionally or as a discrete object."
Oddly enough, in the Zeta function, I think it rather elegantly shows that 1 is not a prime number!
There are all kinds of infinities.
Take a line. Put two points on it.
There is an infinity of points between the two points you created, and there are also infinities on the line on the outsides of the points. Is the infinity of points in the middle somehow less than the infinities of the other segments? One would think. However...
Take a line. Put two points on it.
There is an infinity of points between the two points you created, and there are also infinities on the line on the outsides of the points. Is the infinity of points in the middle somehow less than the infinities of the other segments? One would think. However...
edit on 20-2-2019 by Blue Shift because: (no reason given)
Just a mildly related story but here it is:
Some time back there was industrial action at the oil refineries that resulted in a fuel shortage so the state government decreed that only vehicles with an even final number on their number plate could be served one day then odd numbers the next and so on in an attempt to make it less chaotic in the queues waiting to be served.
Fistfights were breaking out when those with a '0' tried to join the 'evens' queue because '0 is not an even number, maybe not a number at all' so the government had to decree that it was an even number. Not sure if that was ever actually written into legislation though but looks a precedent to me
Some time back there was industrial action at the oil refineries that resulted in a fuel shortage so the state government decreed that only vehicles with an even final number on their number plate could be served one day then odd numbers the next and so on in an attempt to make it less chaotic in the queues waiting to be served.
Fistfights were breaking out when those with a '0' tried to join the 'evens' queue because '0 is not an even number, maybe not a number at all' so the government had to decree that it was an even number. Not sure if that was ever actually written into legislation though but looks a precedent to me
a reply to: Archivalist
But wait, between any two numbers, there is another number, forever.
Isn't that a form of infinity too?
Infinity doesn't just mean big forever, it means between forever also.
But wait, between any two numbers, there is another number, forever.
Isn't that a form of infinity too?
Infinity doesn't just mean big forever, it means between forever also.
Must you believe it?
The 12-year-old student was struggling to grasp the basic principles of algebra. His teacher presented the class with a seemingly straightforward algebraic calculation.
“Let x=y and let them both have the value of 1,” he began.
‘So far so good,’ thought the student.
After four lines of what looked like logical calculation, however, the teacher produced a startling result: “Therefore, 2=1!”
“Disprove that,” he challenged his bemused students.
With his very limited knowledge of algebra, the young student could not see how to disprove it. Every step in the calculation looked perfectly valid. Should he, then, believe this strange conclusion? After all, his teacher was much more versed in mathematics than he was. Of course he should not! ‘I do not have to disprove this,’ he thought to himself. ‘Common sense tells me that this is absurd.’ (Proverbs 14:15, 18) He knew that neither his teacher nor any of his classmates were going to exchange two dollars for one!
In time the algebra student did find the flaw in the computation. Meanwhile, the experience taught him a valuable lesson. Even when someone with vastly superior knowledge presents a carefully crafted and seemingly unassailable argument, a listener need not believe a foolish conclusion simply because he cannot disprove it at the time. The student was actually following a very practical Bible principle found at 1 John 4:1—not to believe too quickly everything you hear, even when it appears to come from an authoritative source.
This does not mean that you should stubbornly stick to preconceived ideas. It is a mistake to close your mind to information that could adjust mistaken views. But neither should you be “quickly shaken from your reason” in the face of pressure from someone who claims to have great knowledge or authority. (2 Thessalonians 2:2) The teacher, of course, was merely playing a trick on his students. Sometimes, though, things are not so innocent. People can be extremely “cunning in contriving error.”—Ephesians 4:14; 2 Timothy 2:14, 23, 24.
Are experts always right?
However knowledgeable they may be, experts in any field may have conflicting ideas and shifting opinions. Take, for example, the ongoing debate in medical science on something as basic as causes of illness. “The relative importance of nature versus nurture in illness forms the fabric of heated debate among scientists,” writes a professor of medicine at Harvard University. Those in what has been called the determinist camp believe strongly that our genes play a decisive role in our susceptibility to various diseases. Others, however, contend that the environment and life-style are the major factors in human pathology. Both sides are quick to cite studies and statistics to support their case. Nonetheless, the debate continues.
The most renowned of thinkers have been proved wrong again and again, even though what they taught seemed at the time to be beyond dispute. Philosopher Bertrand Russell described Aristotle as one of “the most influential of all philosophers.” Yet, Russell also pointed out that many of Aristotle’s doctrines were “wholly false.” “Throughout modern times,” he wrote, “practically every advance in science, in logic, or in philosophy has had to be made in the teeth of opposition from Aristotle’s disciples.”—History of Western Philosophy.
“The Falsely Called ‘Knowledge’”
The early Christians likely met many who were disciples of the noted Greek philosophers, such as Socrates, Plato, and Aristotle. Educated people of the day regarded themselves as intellectually superior to most of the Christians. Not many of Jesus’ disciples were considered “wise in a fleshly way.” (1 Corinthians 1:26) In fact, those schooled in the philosophies of the day thought that what the Christians believed was simply “foolishness” or “sheer nonsense.”—1 Corinthians 1:23; Phillips.
If you were among those early Christians, would you have been impressed by the persuasive arguments of the intellectual elite of the day or overawed by their display of wisdom? (Colossians 2:4) There would have been no reason for that, according to the apostle Paul. He reminded Christians that Jehovah views “the wisdom of the wise men” and the “intelligence of the intellectual men” of the day as foolish. (1 Corinthians 1:19) “What,” he asked, “have the philosopher, the writer and the critic of this world to show for all their wisdom?” (1 Corinthians 1:20, Phillips) Despite all their intellectual brilliance, the philosophers, the writers, and the critics of Paul’s day had produced no real answer to mankind’s problems.
So Christians learned to avoid what the apostle Paul said were “the contradictions of the falsely called ‘knowledge.’” (1 Timothy 6:20) In some cases the wise men of their day were, in fact, “suppressing the truth” and ignoring the evidence around them that there is a God. “Although asserting they were wise, they became foolish,” wrote the apostle Paul. Because they rejected the truth about God and his purpose, “they became empty-headed in their reasonings and their unintelligent heart became darkened.”—Romans 1:18-22; Jeremiah 8:8, 9.
Those who assert that they are wise often come up with conclusions like “There is no God” or “The Bible is not to be trusted” or that “Nothing is something.” Such ideas are just as foolish in God’s eyes as concluding that “2=1” or that “0=infinity.” (1 Corinthians 3:19) Whatever authority people may arrogate to themselves, you do not have to accept their conclusions if they violate common sense. In the final analysis, the wise course is always to “let God be found true, though every man be found a liar.”—Romans 3:4.
1 Corinthians 3:19
19 For the wisdom of this world is foolishness with God, for it is written: “He catches the wise in their own cunning.”
Common Sense—Why So Uncommon?
The 12-year-old student was struggling to grasp the basic principles of algebra. His teacher presented the class with a seemingly straightforward algebraic calculation.
“Let x=y and let them both have the value of 1,” he began.
‘So far so good,’ thought the student.
After four lines of what looked like logical calculation, however, the teacher produced a startling result: “Therefore, 2=1!”
“Disprove that,” he challenged his bemused students.
With his very limited knowledge of algebra, the young student could not see how to disprove it. Every step in the calculation looked perfectly valid. Should he, then, believe this strange conclusion? After all, his teacher was much more versed in mathematics than he was. Of course he should not! ‘I do not have to disprove this,’ he thought to himself. ‘Common sense tells me that this is absurd.’ (Proverbs 14:15, 18) He knew that neither his teacher nor any of his classmates were going to exchange two dollars for one!
In time the algebra student did find the flaw in the computation. Meanwhile, the experience taught him a valuable lesson. Even when someone with vastly superior knowledge presents a carefully crafted and seemingly unassailable argument, a listener need not believe a foolish conclusion simply because he cannot disprove it at the time. The student was actually following a very practical Bible principle found at 1 John 4:1—not to believe too quickly everything you hear, even when it appears to come from an authoritative source.
This does not mean that you should stubbornly stick to preconceived ideas. It is a mistake to close your mind to information that could adjust mistaken views. But neither should you be “quickly shaken from your reason” in the face of pressure from someone who claims to have great knowledge or authority. (2 Thessalonians 2:2) The teacher, of course, was merely playing a trick on his students. Sometimes, though, things are not so innocent. People can be extremely “cunning in contriving error.”—Ephesians 4:14; 2 Timothy 2:14, 23, 24.
Are experts always right?
However knowledgeable they may be, experts in any field may have conflicting ideas and shifting opinions. Take, for example, the ongoing debate in medical science on something as basic as causes of illness. “The relative importance of nature versus nurture in illness forms the fabric of heated debate among scientists,” writes a professor of medicine at Harvard University. Those in what has been called the determinist camp believe strongly that our genes play a decisive role in our susceptibility to various diseases. Others, however, contend that the environment and life-style are the major factors in human pathology. Both sides are quick to cite studies and statistics to support their case. Nonetheless, the debate continues.
The most renowned of thinkers have been proved wrong again and again, even though what they taught seemed at the time to be beyond dispute. Philosopher Bertrand Russell described Aristotle as one of “the most influential of all philosophers.” Yet, Russell also pointed out that many of Aristotle’s doctrines were “wholly false.” “Throughout modern times,” he wrote, “practically every advance in science, in logic, or in philosophy has had to be made in the teeth of opposition from Aristotle’s disciples.”—History of Western Philosophy.
“The Falsely Called ‘Knowledge’”
The early Christians likely met many who were disciples of the noted Greek philosophers, such as Socrates, Plato, and Aristotle. Educated people of the day regarded themselves as intellectually superior to most of the Christians. Not many of Jesus’ disciples were considered “wise in a fleshly way.” (1 Corinthians 1:26) In fact, those schooled in the philosophies of the day thought that what the Christians believed was simply “foolishness” or “sheer nonsense.”—1 Corinthians 1:23; Phillips.
If you were among those early Christians, would you have been impressed by the persuasive arguments of the intellectual elite of the day or overawed by their display of wisdom? (Colossians 2:4) There would have been no reason for that, according to the apostle Paul. He reminded Christians that Jehovah views “the wisdom of the wise men” and the “intelligence of the intellectual men” of the day as foolish. (1 Corinthians 1:19) “What,” he asked, “have the philosopher, the writer and the critic of this world to show for all their wisdom?” (1 Corinthians 1:20, Phillips) Despite all their intellectual brilliance, the philosophers, the writers, and the critics of Paul’s day had produced no real answer to mankind’s problems.
So Christians learned to avoid what the apostle Paul said were “the contradictions of the falsely called ‘knowledge.’” (1 Timothy 6:20) In some cases the wise men of their day were, in fact, “suppressing the truth” and ignoring the evidence around them that there is a God. “Although asserting they were wise, they became foolish,” wrote the apostle Paul. Because they rejected the truth about God and his purpose, “they became empty-headed in their reasonings and their unintelligent heart became darkened.”—Romans 1:18-22; Jeremiah 8:8, 9.
Those who assert that they are wise often come up with conclusions like “There is no God” or “The Bible is not to be trusted” or that “Nothing is something.” Such ideas are just as foolish in God’s eyes as concluding that “2=1” or that “0=infinity.” (1 Corinthians 3:19) Whatever authority people may arrogate to themselves, you do not have to accept their conclusions if they violate common sense. In the final analysis, the wise course is always to “let God be found true, though every man be found a liar.”—Romans 3:4.
1 Corinthians 3:19
19 For the wisdom of this world is foolishness with God, for it is written: “He catches the wise in their own cunning.”
Common Sense—Why So Uncommon?
...
Common sense seems to be so lacking in today’s world that an observant man once noted, ‘Common sense, in truth, is very uncommon.’ ...
edit on 21-2-2019 by whereislogic because: (no reason given)
new topics
-
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order: 9 minutes ago -
Ireland VS Globalists
Social Issues and Civil Unrest: 40 minutes ago -
Biden "Happy To Debate Trump"
Mainstream News: 1 hours ago -
RAAF airbase in Roswell, New Mexico is on fire
Aliens and UFOs: 1 hours ago -
What is the white pill?
Philosophy and Metaphysics: 2 hours ago -
Mike Pinder The Moody Blues R.I.P.
Music: 3 hours ago -
Putin, Russia and the Great Architects of the Universe
ATS Skunk Works: 6 hours ago -
A Warning to America: 25 Ways the US is Being Destroyed
New World Order: 11 hours ago
top topics
-
President BIDEN's FBI Raided Donald Trump's Florida Home for OBAMA-NORTH KOREA Documents.
Political Conspiracies: 16 hours ago, 35 flags -
A Warning to America: 25 Ways the US is Being Destroyed
New World Order: 11 hours ago, 20 flags -
Mike Pinder The Moody Blues R.I.P.
Music: 3 hours ago, 7 flags -
What is the white pill?
Philosophy and Metaphysics: 2 hours ago, 5 flags -
Biden "Happy To Debate Trump"
Mainstream News: 1 hours ago, 5 flags -
RAAF airbase in Roswell, New Mexico is on fire
Aliens and UFOs: 1 hours ago, 4 flags -
Putin, Russia and the Great Architects of the Universe
ATS Skunk Works: 6 hours ago, 3 flags -
Ireland VS Globalists
Social Issues and Civil Unrest: 40 minutes ago, 2 flags -
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order: 9 minutes ago, 0 flags
active topics
-
Putin, Russia and the Great Architects of the Universe
ATS Skunk Works • 23 • : RussianTroll -
Biden "Happy To Debate Trump"
Mainstream News • 21 • : PorkChop96 -
A Warning to America: 25 Ways the US is Being Destroyed
New World Order • 28 • : SchrodingersRat -
What is the white pill?
Philosophy and Metaphysics • 17 • : RealityDestroyer -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media • 280 • : Vermilion -
Ireland VS Globalists
Social Issues and Civil Unrest • 3 • : nugget1 -
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order • 0 • : FlyInTheOintment -
Candidate TRUMP Now Has Crazy Judge JUAN MERCHAN After Him - The Stormy Daniels Hush-Money Case.
Political Conspiracies • 793 • : matafuchs -
Is AI Better Than the Hollywood Elite?
Movies • 22 • : 5thHead -
King Charles 111 Diagnosed with Cancer
Mainstream News • 324 • : Oldcarpy2
