It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
11
share:
Hi ATS!
Math gets me excited when big ideas are approached differently with huge results.
A mathematician does not usually directly challenge a problem. That is why we have not seen a solution to math's biggest problem, the Riemann Hypothesis (RH). While stated simply, the problem is in the details. First, the Riemann Zeta (Rz) function looks like a simple addition of all the numbers in logarithm form. A quick glance give you the impression it heads off to infinity. But because the equation is of the form: 1/1^2 + 1/2^2 + 1/3^2 + ... (infinity), as the numbers get larger, the values get smaller. Mathematicians are rather picky about leaving things as estimates (I am sure somebody here will point out, "Hey Rz is of the form 1/1^-s + 1/2^-s + 1/3^-s + ..." which is true! But it also has to be extended across all numbers except 1, where it shoots off to infinity. I just said it was "of the form"). When extended across all real numbers there is a portion the equation is stated:
s = σ + it.
That little term, σ, is called sigma. When the entire function is set to zero, the numerical solution to the big mess of equations are either -2, -4, -6,... (known as trivial zeros of the function); or, the sigma is replaced by 1/2. The values of t wander up the imaginary plane. These non-trivial zeros of the Riemann zeta function are also prime numbers!
Source: Wikipedia
In the equation, that means: s = 1/2 + it
This little statement, scribbled in the margin of Riemann's notes, has driven mathematicians mad (see Nash and A Beautiful Mind) and has been unsolved for over 160 years. The Rz function is a very powerful tool for mathematical analysis. Solving Riemann (as it is called) would be a life changing moment for any mathematician.
This post is not about RH! But it is too.
arXiv.org (arXiv:1708.06607v4) - A novel approach to the Lindelöf hypothesis.
The Riemann-Hilbert problem has calculated exponents (I know, eyes glazing over. Hang in there!), eta and eta-squared, which are used in the Big-Oh estimate of Riemann zeta function for large values of t. The actual notation reads, O(1/2t^eta). That is the estimation of how t grows when calculating Rz. Fokas went back to that earlier problem and did a book end calculations, calculated eta and eta-squared, then showed in his paper that it holds for all values eta, therefore proving the Lindelöf's hypothesis!
This may spur new techniques and approaches to RH.
This is probably one of the biggest steps I have been witness to after knowing (even if just a brief introduction to) complex analysis! I am excited about this as discoveries like these tend to spur other mathematicians forward.
Math gets me excited when big ideas are approached differently with huge results.
A mathematician does not usually directly challenge a problem. That is why we have not seen a solution to math's biggest problem, the Riemann Hypothesis (RH). While stated simply, the problem is in the details. First, the Riemann Zeta (Rz) function looks like a simple addition of all the numbers in logarithm form. A quick glance give you the impression it heads off to infinity. But because the equation is of the form: 1/1^2 + 1/2^2 + 1/3^2 + ... (infinity), as the numbers get larger, the values get smaller. Mathematicians are rather picky about leaving things as estimates (I am sure somebody here will point out, "Hey Rz is of the form 1/1^-s + 1/2^-s + 1/3^-s + ..." which is true! But it also has to be extended across all numbers except 1, where it shoots off to infinity. I just said it was "of the form"). When extended across all real numbers there is a portion the equation is stated:
s = σ + it.
That little term, σ, is called sigma. When the entire function is set to zero, the numerical solution to the big mess of equations are either -2, -4, -6,... (known as trivial zeros of the function); or, the sigma is replaced by 1/2. The values of t wander up the imaginary plane. These non-trivial zeros of the Riemann zeta function are also prime numbers!
The real part of every non-trivial zero of the Riemann zeta function is 1/2
Source: Wikipedia
In the equation, that means: s = 1/2 + it
This little statement, scribbled in the margin of Riemann's notes, has driven mathematicians mad (see Nash and A Beautiful Mind) and has been unsolved for over 160 years. The Rz function is a very powerful tool for mathematical analysis. Solving Riemann (as it is called) would be a life changing moment for any mathematician.
This post is not about RH! But it is too.
Lindelöf's hypothesis, one of the most important open problems in the history of mathematics, states that for large t, Riemann's zeta function ζ(1/2+it) is of order O(t^ε) for any ε>0. It is well known that for large t, the leading order asymptotics of the Riemann zeta function can be expressed in terms of a transcendental exponential sum. The usual approach to the Lindelöf hypothesis involves the use of ingenious techniques for the estimation of this sum.
arXiv.org (arXiv:1708.06607v4) - A novel approach to the Lindelöf hypothesis.
“My approach was completely different from the usual approaches used,” Fokas said. “I first embed the R zeta function inside a bigger problem, namely I find that the R zeta function satisfies a very important problem in complex analysis called the Riemann-Hilbert problem. Then, I compute the large t behavior of this problem. Besides being conceptually novel, this approach is technically very hard due to the analysis of the aforementioned Riemann-Hilbert problem.”
-Athanassios Fokas, Mathematicia n-M.D. solves one of the greatest open problems in the history of mathematics (blog)
The Riemann-Hilbert problem has calculated exponents (I know, eyes glazing over. Hang in there!), eta and eta-squared, which are used in the Big-Oh estimate of Riemann zeta function for large values of t. The actual notation reads, O(1/2t^eta). That is the estimation of how t grows when calculating Rz. Fokas went back to that earlier problem and did a book end calculations, calculated eta and eta-squared, then showed in his paper that it holds for all values eta, therefore proving the Lindelöf's hypothesis!
This may spur new techniques and approaches to RH.
If I were to awaken after having slept for a thousand years, my first question would be: Has the Riemann hypothesis been proven?
-David Hilbert, Wikiquote
This is probably one of the biggest steps I have been witness to after knowing (even if just a brief introduction to) complex analysis! I am excited about this as discoveries like these tend to spur other mathematicians forward.
edit on 26-6-2018 by TEOTWAWKIAIFF because: formatting
Fokas is a world expert in asymptotics, an applied mathematical domain which helps scientists answer questions about the behavior of functions when a parameter is very large. His proof of Lindelöf also means a breakthrough in understanding algorithmic complexity, a very important topic in computer science. Knowing the complexity of algorithms allows us to answer questions such as how long will a program run on an input? How much space will it take? Is the problem solvable?
Source: quote url
This is the "why" it matters. That and the "is the problem solvable". This may lead to classification of NP and P problems. And with quantum algorithms coming down the pipe we may get a better handle on what needs to be handed off to quantum computers and what can churn along in super computers (computing time being expensive).
They moved the story on the USC page so took the long way around (we are not supposed to start threads from blogs). I hope I made sense! All error and misspoke, misstypes, and complete lack of understanding of complex analysis are my own.
This guy is no slouch! He got the same award Hawking did and is considered an expert in asymptotics which the eta and eta-squared are found.
Quick note: I have had a MS update applied, against my will, that kills my Citrix vNIC address (to prevent people from spoofing IP addresses). And it
has nothing to do with my network connection. Anyway, been to busy to track down the other MS Patch that corrects the original path (which was
identified earlier this year but was re-released by MS again for some unknown reason). That means, limited interweb time so I have been filling up my
browser with stuff to read, switching back to the other network, and reading, well, basically math and physics stuff.
Back to OP...
phys.org, Aug. 7, 2018 - Mathematician discusses solving a seemingly unsolvable equation.
The "solving it loops" is really interesting! What is being described is integration in recursion form. They had to do seven or eight levels of this recursion integration using formula substitution (a common technique usually with the mathematician's name who first figured it out given as the method). The main investigator ran into another mathematician who had a computer program written that does the symbolic math (it does not just spit out an answer, it manipulates the symbols and shows intermediary steps). Using the program, it verified the first four "loops" and then was used to calculate the next three loops. Then they noticed a pattern emerging. They did the work and defined a new function called the Nielson function:
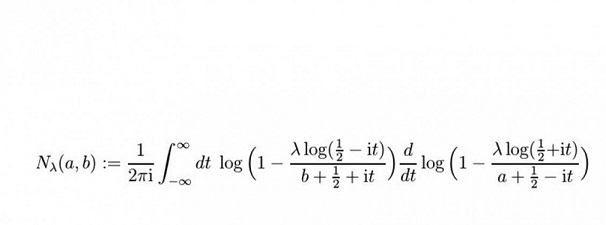
(this all the same source using most of their terms).
One thing should be noticeable, it is a complex equation! Our friend 1/2 + it is there. The other is this goes from negative infinity to positive infinity. If truly is a step function where one result feeds into the next and it does describe elementary particles then we are really close to Riemann again!
phys.org - New insight into proving math's million-dollar problem: the Riemann hypothesis (Update).
Which shows that the isomorphic zeta function (i.e., it was extended into the entire real numbers using analytic techniques) is actually equivalent to the eigenvalues of a matrix operator (in quantum mechanics, that matrix is an energy state level called a Hamiltonian). The guys who solved this now have the conjecture named after them, Berry-Keating conjecture. It basically says that the non-trivial zeroes of the zeta function there exists a Hamiltonian describing it. Or in other words, math describes our reality from the quantum on up. More specifically, prime numbers!
Prime numbers are the result of the zeros of the zeta function! Look at Nielson function, it seems there might be a path to the B-K conjecture. Prime numbers, like those already found in nature.
BBC.com - Nature's hidden prime number code.
It is all prime loops, man!!
Back to OP...
What can the equation be used for?
It's about a mathematical understanding of quantum field theories. These belong to the field of physics and play a part in large-scale experiments such as those carried out at CERN. The aim is to mathematically describe elementary particles, i.e. the smallest known components of matter. But this is so complicated that, instead, imaginary particles are described mathematically which have certain properties of the real particles. The hope is that one day the real particles can be described using the methods established in this way.
After working on the problem for 10 years, you experienced a breakthrough this year. How did that come about?
Towards the end of May, I tried out an idea for which my Ph.D. student, Alexander Hock, provided the decisive impulse. I worked out a new equation – simpler than the previous one – and began to solve it in loops. What this means is that you approach the solution step by step, i.e. loop by loop, by calculating the left side of the equation in each previous step and using it for the right side of the equation in the next step.
phys.org, Aug. 7, 2018 - Mathematician discusses solving a seemingly unsolvable equation.
The "solving it loops" is really interesting! What is being described is integration in recursion form. They had to do seven or eight levels of this recursion integration using formula substitution (a common technique usually with the mathematician's name who first figured it out given as the method). The main investigator ran into another mathematician who had a computer program written that does the symbolic math (it does not just spit out an answer, it manipulates the symbols and shows intermediary steps). Using the program, it verified the first four "loops" and then was used to calculate the next three loops. Then they noticed a pattern emerging. They did the work and defined a new function called the Nielson function:
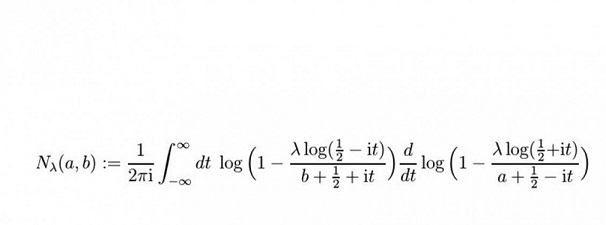
(this all the same source using most of their terms).
One thing should be noticeable, it is a complex equation! Our friend 1/2 + it is there. The other is this goes from negative infinity to positive infinity. If truly is a step function where one result feeds into the next and it does describe elementary particles then we are really close to Riemann again!
phys.org - New insight into proving math's million-dollar problem: the Riemann hypothesis (Update).
Which shows that the isomorphic zeta function (i.e., it was extended into the entire real numbers using analytic techniques) is actually equivalent to the eigenvalues of a matrix operator (in quantum mechanics, that matrix is an energy state level called a Hamiltonian). The guys who solved this now have the conjecture named after them, Berry-Keating conjecture. It basically says that the non-trivial zeroes of the zeta function there exists a Hamiltonian describing it. Or in other words, math describes our reality from the quantum on up. More specifically, prime numbers!
Prime numbers are the result of the zeros of the zeta function! Look at Nielson function, it seems there might be a path to the B-K conjecture. Prime numbers, like those already found in nature.
BBC.com - Nature's hidden prime number code.
It is all prime loops, man!!
And now, there's a rumor circulating that this 160-year-old mega-problem might finally be solved – by British-Lebanese geometer Sir Michael Atiyah.
Intriguingly, by citing von Neumann, Hirzebruch and Dirac, Atiyah hints that his "simple proof" draws influence from the world of quantum mechanics. There's no doubt we should keep a healthy dose of skepticism until the proof is presented and reviewed. However, if it holds up, we could be about to see the most significant discovery in mathematics for over a quarter of a century.
IFLScience.com, Sept. 20, 2018 - A Mathematician Claims He's Found A "Simple Proof" Of This Million-Dollar Problem.
Sir Michael Atiyah announced, via twitter, that he will be giving a lecture on Monday, September 24, 9:45 - 10:30am, to present his solution of the one, the only, Riemann Hypothesis!
I read up on the Clay Institute, Millennium Prize. First, you have to have your paper submitted and approved for publication to certain places. Then a committee has to verify your paper (they can take a couple years to do so, too!), in addition to peer review. Then, at the Clay Institute's discretion, they may award you the "million dollar prize".
Great thing is, Monday is only a few days away. So this is a "wait and see".
For a peek at how QM and Riemann cross paths:
Quantamagazine.org - Physicists Attack Math’s $1,000,000 Question.
edit on 20-9-2018 by TEOTWAWKIAIFF because: correction
The “boundary condition” is imposing an identification with zeta zeros by fiat, so the linkage of any of this to RH is basically circular. The paper at best just redefines the problem, without providing any genuine new insight. More specifically, as the experience of more than 100 years has shown, there are a zillion ways to recast RH without providing any real progress; this is yet another (if it makes any rigorous sense, which it does not yet do, yet the absence of rigor is not the reason for skepticism about the value of this paper, whatever the pedigree of the authors may be).
One has to find a way of encoding the zeta function that is not tautological (unlike the case here), and that is where deep input from number theory would have to come in. This is really the essential point that all papers of this sort fail to recognize.
Real insight into the structures surrounding RH have arisen over the past decades, such as the work of Grothendieck and Deligne in the function field analogue that provided a spectral interpretation through the development of striking new tools inspired by novel insights of Weil. In particular, the appearance of the appropriate zeta functions in such settings is not imposed by fiat, but is the outcome of a massive amount of highly non-trivial constructions and arguments. In another direction, compelling evidence and insight has come from the “random matrix theory” of the past couple of decades (work of Katz-Sarnak et al.) was inspired by observations originating with Dyson merged with work of the number theorist Montgomery.
Number theorists making a major advance on the puzzles of quantum gravity without providing an identifiable new physical insight is about as likely as physicists making a real advance towards RH without providing an identifiable new number-theoretic insight.
math.columbia.edu - Some Math and Physics Interactions.
Ouch! This was a response to author's critique of the Quantamagazine.org article (basically agreeing that jumping to QM to prove a math problem is probably not going to work).
They point out that re-wording RH in QM does "solve" the problem. A very nice, if blunt, observation.
I am not holding my breath on a "simple proof" to Riemann. As the Lindelöf's hypothesis of the OP shows, it takes an act of brilliance (and usually a group of people) to solve a problem.
Abstract : The Riemann Hypothesis is a famous unsolved problem dating from 1859. I will present a simple proof using a radically new approach. It is based on work of von Neumann (1936), Hirzebruch (1954) and Dirac (1928).
Sir Michael Atiyah, twitter
The competing mathematical strategies are manifest in a more recent discussion concerning the mathematical foundations of quantum mechanics. In the preface to von Neumann's treatise (1955) on that topic, he notes that Dirac provides a very elegant and powerful formal framework for quantum mechanics, but complains about the central role in that framework of an “improper function with self-contradictory properties,” which he also characterizes as a “mathematical fiction.” He is referring to the Dirac delta function, which has the following incompatible properties: it is defined over the real line, is zero everywhere except for one point at which it is infinite, and yields unity when integrated over the real line. Von Neumann promotes an alternative framework, which he characterizes as being “just as clear and unified, but without mathematical objections.” He emphasizes that his framework is not merely a refinement of Dirac's; rather, it is a radically different framework that is based on Hilbert's theory of operators.
stanford.edu - Quantum Theory: von Neumann vs. Dirac.
And Friedrich Hirzebruch wrote Topological Methods in Algebraic Geomtry.
We are supposed to believe that a "simple proof" of the Riemann Hypothesis just falls out from contradictory QM views using different maths via algebraic geometry??!!
Here is the Riemann zeta function using a Hamiltonian from the Hilbert-Polya conjecture (Wikipedia: RH - Operator theory):
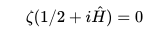
That says the eigenvalues (scalar solution to a matrix operator, Hamiltonian, H, i.e., corresponding to where zeta(x) = 0) are equivalent which has nothing at all to do with Dirac!
I recognize the symbols, follow some of the operations, but not into real analysis and complex functions. I am at the limit of my knowledge and not sure anything "simple" can be said the zeta function.
I am a feared that Sir Michael Atiyah may be over stating something here.
Popcorn is ready!
Atiyah is well aware of this history of failure. “Nobody believes any proof of the Riemann hypothesis, let alone a proof by someone who’s 90,” he says, but he hopes his presentation will convince his critics.
In it, he pays tribute to the work of two great 20th century mathematicians, John von Neumann and Friedrich Hirzebruch, whose developments he claims laid the foundations for his own proposed proof. “It fell into my lap, I had to pick it up,” he says.
New Scientist contacted a number of mathematicians to comment on the claimed proof, but all of them declined.
newscientist.com, Sept. 21, 2018 - Famed mathematician claims proof of 160-year-old Riemann hypothesis.
That is not a good sign! Seems the mathematicians already know this lecture will go over like a lead balloon!
Here is commentary over at reddit: HLF 2018 Atiyah Lecture: "The Riemann Hypothesis"
Nice to know I got some of my thought in line with real mathematicians! And now to go check out the QM side of things and do some reading!
So TEOT, what the heck is the Riemann Hypothesis?
Here is basic crash course introduction to complex analysis.
The natural numbers are just the integers we count with:
N = [0, 1, 2, 3, ...]
They can represented as a flat line. In between these numbers other numbers can be defined as well. If you split the number at its halfway point between zero and one you get 1/2. Add two ½ together and you get one. Rational numbers, like ½, and irrational numbers, sqrt(2), also exist in this in between integers, Z, on this line. This constitutes the Real number line.
Z = [-3, -2, -1, 0, 1, 2, 3, ...]
Numbers are defined by the company they keep with these set notations: N, Z, Q (real numbers) P (complex)
A function, f, takes a given input, x (let's say), and gives a different output depending upon what math operators tell it to do. It is denoted, f(x), and is pronounced, “f of x” (just like Mulder!). Certain function reappear so often they are given their own symbol. Certain numbers do to, like pi, for the irrational number, 3.1415… and the one about to be introduced.
The problem came around that answers to mathematical questions kept giving answers of the square root of -1. The problem is there is no such number! Some mathematicians called that number “imaginary” because it did not exist. So it was declared to exist!
i^2 = -1
Complex number from P are defined: a + bi
But how do you graph an imaginary number? Not to fear! See you can extend the real number line in the vertical direction creating something known as the complex plane. When b = 0, the “imaginary” part disappears. a moves us forward and backward along the real number line, while bi moves you above it or below it.
Remember “f of x”? There is nothing stopping you from using a + bi in the function and when done you are doing complex analysis! Of course that is not the only condition but that is the general gist. Using complex numbers opened up new doors of inquiry into math and problems involving difficult function became solvable using the tools of complex analysis.
In complex analysis the function itself is generally not very interesting except at certain points called a “singularity” in general. The real interesting places are called “poles” which is a type of singularity. Where the f(a+bi) = 0 are also of special interest and are known as the “zero of the function”.
Riemann’s Zeta Function
One function that got its own letter is zeta, ζ, in Greek. It is the inverse sum of integers raised to an integer power. Bernhard Riemann was looking at the zeta function and extended it to the complex plane. The formula is: ζ(n) and defined as:
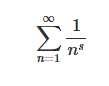
While preparing for a lecture, he wrote that he believed that this extended zeta function has a real part, (the a in the a + bi, which is represented by “s” in the above formula), that was always equal to ½ for non-trivial zeroes (trivial zeroes are on the real number line and are equal to the negative multiples of 2). He wrote that in the margins of his notes, gave his lecture but did not mention his belief. He also did not solve it and moved onto to work on another problem then died. The non-trivial zeroes of the Riemann zeta function also are equal to the prime numbers. The generalized Riemann Hypothesis is what was just stated and there is a stronger version.
Euler figured out how to “sieve” the zeta function which removed multiples of numbers like 2x3, 2x4, 2x5, etc. He applied this to all remaining odd numbers after removing the even numbers. From infinite addition what resulted is rather amazing (I had to do this for myself several time to “get it”) (source: Wikipedia)
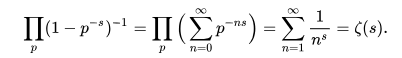
The capital Pi is called the primorial function. In math notation it saying, "take a prime number, p, and multiply it to the next one, do this to infinity". In other words, if you subtract out the multiples of numbers (known as "composites") you end up with multiplication of the prime numbers!
The proof of Riemann (as the “hypothesis” is usually left off or is simply abbreviated, RH), has eluded mathematicians for over 160 years.
The OP is about a related problem. As prime numbers grow larger, the gap between prime numbers also grows. We are talking really huge numbers here. Complex analysis allows mathematicians to use all the tools of the math trade to address these huge numbers. The field is known as asymptotic analysis and specifically pays attention to boundaries. The numbers are so huge they use “Big O” notation which means “order of magnitude”. We all know the difference between 10 and 100, or, 1000 and 1000000, but these numbers are even bigger! Like, 100 000 000 000 000 000 000 000 and it’s squared form! That is big O territory. The Lindelof hypothesis concerned the growth rate of Riemann’s zeta function (to be certain, the RZ was analytically extended across the complex plane so the neat equation has more bolted onto it than what is seen above. And there are other representations including one using pi). The LH is actually implied by RH but the reverse is not true so solving LH does not solve RH but as Fokas said, mathematicians no longer have to spend their time on it either.
My thoughts. Since the complex plane is created using i in the vertical it is kind indicative of what the Euler Product is telling us. It is the primorial function where all prime numbers are multiplied together: 2x3x5x7x11…, such that we only meet each prime once. Because zeta is an inversed sum, ½, is our first time we see, “2”, next prime we see is “3” but to get to it we use, 2x3, but in inverted form, such that bi is sieving out the first occurrence of 3 like the Euler product shows before zeta goes off roaming the complex plane and plotting out the composite numbers. It also why the trivial numbers are negative multiples of two.
But I just thought of that today. I am sure somebody else has too if a knuckle head like me can think of it!
Disclaimer: Do not use this post to perform actual math! It is for demonstration purposes only! Consult your interomathematician or analytic specialist to balance your check book. All gross misstatements are my own.
Here is basic crash course introduction to complex analysis.
The natural numbers are just the integers we count with:
N = [0, 1, 2, 3, ...]
They can represented as a flat line. In between these numbers other numbers can be defined as well. If you split the number at its halfway point between zero and one you get 1/2. Add two ½ together and you get one. Rational numbers, like ½, and irrational numbers, sqrt(2), also exist in this in between integers, Z, on this line. This constitutes the Real number line.
Z = [-3, -2, -1, 0, 1, 2, 3, ...]
Numbers are defined by the company they keep with these set notations: N, Z, Q (real numbers) P (complex)
A function, f, takes a given input, x (let's say), and gives a different output depending upon what math operators tell it to do. It is denoted, f(x), and is pronounced, “f of x” (just like Mulder!). Certain function reappear so often they are given their own symbol. Certain numbers do to, like pi, for the irrational number, 3.1415… and the one about to be introduced.
The problem came around that answers to mathematical questions kept giving answers of the square root of -1. The problem is there is no such number! Some mathematicians called that number “imaginary” because it did not exist. So it was declared to exist!
i^2 = -1
Complex number from P are defined: a + bi
But how do you graph an imaginary number? Not to fear! See you can extend the real number line in the vertical direction creating something known as the complex plane. When b = 0, the “imaginary” part disappears. a moves us forward and backward along the real number line, while bi moves you above it or below it.
Remember “f of x”? There is nothing stopping you from using a + bi in the function and when done you are doing complex analysis! Of course that is not the only condition but that is the general gist. Using complex numbers opened up new doors of inquiry into math and problems involving difficult function became solvable using the tools of complex analysis.
In complex analysis the function itself is generally not very interesting except at certain points called a “singularity” in general. The real interesting places are called “poles” which is a type of singularity. Where the f(a+bi) = 0 are also of special interest and are known as the “zero of the function”.
Riemann’s Zeta Function
One function that got its own letter is zeta, ζ, in Greek. It is the inverse sum of integers raised to an integer power. Bernhard Riemann was looking at the zeta function and extended it to the complex plane. The formula is: ζ(n) and defined as:
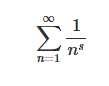
While preparing for a lecture, he wrote that he believed that this extended zeta function has a real part, (the a in the a + bi, which is represented by “s” in the above formula), that was always equal to ½ for non-trivial zeroes (trivial zeroes are on the real number line and are equal to the negative multiples of 2). He wrote that in the margins of his notes, gave his lecture but did not mention his belief. He also did not solve it and moved onto to work on another problem then died. The non-trivial zeroes of the Riemann zeta function also are equal to the prime numbers. The generalized Riemann Hypothesis is what was just stated and there is a stronger version.
Euler figured out how to “sieve” the zeta function which removed multiples of numbers like 2x3, 2x4, 2x5, etc. He applied this to all remaining odd numbers after removing the even numbers. From infinite addition what resulted is rather amazing (I had to do this for myself several time to “get it”) (source: Wikipedia)
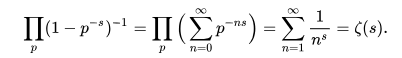
The capital Pi is called the primorial function. In math notation it saying, "take a prime number, p, and multiply it to the next one, do this to infinity". In other words, if you subtract out the multiples of numbers (known as "composites") you end up with multiplication of the prime numbers!
The proof of Riemann (as the “hypothesis” is usually left off or is simply abbreviated, RH), has eluded mathematicians for over 160 years.
The OP is about a related problem. As prime numbers grow larger, the gap between prime numbers also grows. We are talking really huge numbers here. Complex analysis allows mathematicians to use all the tools of the math trade to address these huge numbers. The field is known as asymptotic analysis and specifically pays attention to boundaries. The numbers are so huge they use “Big O” notation which means “order of magnitude”. We all know the difference between 10 and 100, or, 1000 and 1000000, but these numbers are even bigger! Like, 100 000 000 000 000 000 000 000 and it’s squared form! That is big O territory. The Lindelof hypothesis concerned the growth rate of Riemann’s zeta function (to be certain, the RZ was analytically extended across the complex plane so the neat equation has more bolted onto it than what is seen above. And there are other representations including one using pi). The LH is actually implied by RH but the reverse is not true so solving LH does not solve RH but as Fokas said, mathematicians no longer have to spend their time on it either.
My thoughts. Since the complex plane is created using i in the vertical it is kind indicative of what the Euler Product is telling us. It is the primorial function where all prime numbers are multiplied together: 2x3x5x7x11…, such that we only meet each prime once. Because zeta is an inversed sum, ½, is our first time we see, “2”, next prime we see is “3” but to get to it we use, 2x3, but in inverted form, such that bi is sieving out the first occurrence of 3 like the Euler product shows before zeta goes off roaming the complex plane and plotting out the composite numbers. It also why the trivial numbers are negative multiples of two.
But I just thought of that today. I am sure somebody else has too if a knuckle head like me can think of it!
Disclaimer: Do not use this post to perform actual math! It is for demonstration purposes only! Consult your interomathematician or analytic specialist to balance your check book. All gross misstatements are my own.
YouTube: Sir Michael Atiyah Riemann Hypothesis Proof Heidelberg Laureate Forum 2018.
The video is a little over 4 minutes! Let's just say that von Neumann, Hirzebruch, and Dirac, need not be invoked in manner! You could have "the logic of Euclid" for that is about all he did! After fussing about for a few minutes (we join "in progress" and it looks like it is only the good stuff) he gets on with his proof.
One page. That is his proof. It is a "proof by contradiction" where he shows that two mathematical statements about the Riemann Zeta Function (one about a "zero of the zeta function" with Real part 1/2) and about a function T (off of the critical line but in the critical strip, that is also a zero of the Zeta function) cannot be true when manipulated mathematically (he appeals to analytic geometry to create a quadratic equation where one value is zero (original zeta zero) and the other is not (from T) so the solution to the quadratic cannot be a number other than zero, therefor RH).
Honestly, it is sound. But the general RH says "all zeroes of the zeta function have a real part equal to one-half". This is like other papers out there showing percentages of zeroes on/off the critical line. This has been known for sometime. I think it will be a "nice try" but like I said earlier, there is nothing simple about Riemann's zeta function.
I have not seen anything about this in any science web sites yet. I am glad I found his video though!
Well, it looks like the function T in his presentation is actually a real function, not just made up, called the "Todd function".
Science (sciencemag.org) - Skepticism surrounds renowned mathematician’s attempted proof of 160-year-old hypothesis.
motherboard.vice.com - A Mathematician May Have Just Solved a 160-Year-Old, $1 Million Problem.
The Todd function is the major sticking point. It is so obscure that nobody has studied it. It does rely on the fine structure constant which is calculated to be ~1/137 (see Wikipedia for Eddington's instance that it is not approximate but is!). Here is a very famous quote about it:
So, an historic mathematical problem solved by God's constant!!
Step 1 - Collect underpants
Step 2 - ?
Step 3 - Profit!
PS - If for nothing else than another chance to quote Feynman!
The crux of Atiyah’s proof depends on a quantity in physics called the fine structure constant, which describes the strength and nature of electromagnetic interaction between charged particles. By describing this constant using a relatively obscure relationship known as the Todd function, Atiyah claimed to be able to prove the Riemann hypothesis by contradiction.
Science (sciencemag.org) - Skepticism surrounds renowned mathematician’s attempted proof of 160-year-old hypothesis.
Atiyah’s proof claims to answer this question by relying on something he called the “Todd function,” named after the late mathematician and Atiyah’s former teacher J.A. Todd. As Pössel pointed out, the novelty of this function is the source of many mathematicians’ skepticism about Atiyah’s proof.
motherboard.vice.com - A Mathematician May Have Just Solved a 160-Year-Old, $1 Million Problem.
The Todd function is the major sticking point. It is so obscure that nobody has studied it. It does rely on the fine structure constant which is calculated to be ~1/137 (see Wikipedia for Eddington's instance that it is not approximate but is!). Here is a very famous quote about it:
There is a most profound and beautiful question associated with the observed coupling constant, e – the amplitude for a real electron to emit or absorb a real photon. It is a simple number that has been experimentally determined to be close to 0.08542455. (My physicist friends won't recognize this number, because they like to remember it as the inverse of its square: about 137.03597 with about an uncertainty of about 2 in the last decimal place. It has been a mystery ever since it was discovered more than fifty years ago, and all good theoretical physicists put this number up on their wall and worry about it.) Immediately you would like to know where this number for a coupling comes from: is it related to pi or perhaps to the base of natural logarithms? Nobody knows. It's one of the greatest damn mysteries of physics: a magic number that comes to us with no understanding by man. You might say the "hand of God" wrote that number, and "we don't know how He pushed his pencil." We know what kind of a dance to do experimentally to measure this number very accurately, but we don't know what kind of dance to do on the computer to make this number come out, without putting it in secretly!
— Richard Feynman, Richard P. Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. p. 129. ISBN 978-0-691-08388-9.
Source: Wikipedia
So, an historic mathematical problem solved by God's constant!!
Step 1 - Collect underpants
Step 2 - ?
Step 3 - Profit!
PS - If for nothing else than another chance to quote Feynman!
I was reading up on the Fine Structure Constant (FSC). A real, live, constant! Doesn’t matter what or where it is measured, it is still constant!
Not only did this precede quantum mechanics (QM), when QM was formulated, it was still there but in terms of electric charge and Planck’s constant (and the speed of light in a vacuum, C, which we know from the world’s most famous equation, E = mC^2 of Einstein).
Ars Technica-Apr 13, 2018 - A physical constant's value shouldn't depend on how you measure it.
Science News-Apr 12, 2018 - A key constant's new measurement hints 'dark photons' don't exist.
The value has been measured off of a quasar (Forbes, 2017 link), the LHC, the two stories linked above from this year used lasers in the lab, and dang it all, the thing don’t change!
They did a better value: 1/137.035999046 (science news) at 2.4 sigma (Ars Technica).
One would at that point ask the obvious question: Well, how did I get here?
That is where all kinds of stories pop up.
ATS, 2010: Universal "constant" actually varies with time and space (Article).
ATS, 2010: Evidence shows differences in the "fine-structure constant" w/great version of α using Planck's constant.
For a second it appeared the constant was not constant but varied. Then it was realized that it did not vary and the "anomalous measurement" did not show the constant varying.
Enter string theory. They stirred the pot by stating, "IF the FSC varies" but nobody understands what is being said by "IF" up front. They can do the math and string theory works and speculation abounded until the April 2018 reports.
But wait, there's more!
The constant is so shrouded in mystery it is the basis of the sci-fi movie, UFO, starring Gillian Anderson!
ATS, movies – Gillian Anderson in UFO.
In the movie, based on the Chicago O’Hare “cloud punch” event (Mysteriousuniverse.or g – Interview with director of UFO), the FSC is somehow used to fly around the universe in a UFO (I have yet to watch the movie).
Anyhoo, while stuck at work with limited inet access, I have been reading up on this and found this little rabbit hole worthwhile to clutter up the place (and it is not politics!!!). The varying of FSC.
Summary. A proof for the famous Riemann Hypothesis is offered up relying upon an equation that may not even be analytical (in the math sense) which itself relies on a “magic number” that even QED co-creator, Richard Feynman, does not understand. And if that is not enough work for this mystical constant, it is front and center in a movie called, “UFO”, that has X-files written all over it!
FBI, string theory, RH, X-files, UFOs, a real sighting in Chicago, is there anything this constant can’t do?!!
Same as it ever was
Same as it ever was
Same as it ever was
Same as it ever was…
Not only did this precede quantum mechanics (QM), when QM was formulated, it was still there but in terms of electric charge and Planck’s constant (and the speed of light in a vacuum, C, which we know from the world’s most famous equation, E = mC^2 of Einstein).
Ars Technica-Apr 13, 2018 - A physical constant's value shouldn't depend on how you measure it.
Science News-Apr 12, 2018 - A key constant's new measurement hints 'dark photons' don't exist.
The value has been measured off of a quasar (Forbes, 2017 link), the LHC, the two stories linked above from this year used lasers in the lab, and dang it all, the thing don’t change!
They did a better value: 1/137.035999046 (science news) at 2.4 sigma (Ars Technica).
One would at that point ask the obvious question: Well, how did I get here?
That is where all kinds of stories pop up.
ATS, 2010: Universal "constant" actually varies with time and space (Article).
ATS, 2010: Evidence shows differences in the "fine-structure constant" w/great version of α using Planck's constant.
For a second it appeared the constant was not constant but varied. Then it was realized that it did not vary and the "anomalous measurement" did not show the constant varying.
Enter string theory. They stirred the pot by stating, "IF the FSC varies" but nobody understands what is being said by "IF" up front. They can do the math and string theory works and speculation abounded until the April 2018 reports.
But wait, there's more!
The constant is so shrouded in mystery it is the basis of the sci-fi movie, UFO, starring Gillian Anderson!
ATS, movies – Gillian Anderson in UFO.
In the movie, based on the Chicago O’Hare “cloud punch” event (Mysteriousuniverse.or g – Interview with director of UFO), the FSC is somehow used to fly around the universe in a UFO (I have yet to watch the movie).
Anyhoo, while stuck at work with limited inet access, I have been reading up on this and found this little rabbit hole worthwhile to clutter up the place (and it is not politics!!!). The varying of FSC.
Summary. A proof for the famous Riemann Hypothesis is offered up relying upon an equation that may not even be analytical (in the math sense) which itself relies on a “magic number” that even QED co-creator, Richard Feynman, does not understand. And if that is not enough work for this mystical constant, it is front and center in a movie called, “UFO”, that has X-files written all over it!
FBI, string theory, RH, X-files, UFOs, a real sighting in Chicago, is there anything this constant can’t do?!!
Same as it ever was
Same as it ever was
Same as it ever was
Same as it ever was…
a reply to: Groot
People's eyes kind of roll back in their head when they see equations!! That is why editors tell science authors to leave equations out of their books. *face palms*
Seeing the math makes things easier (in my opinion). You can spend a paragraph of words and explaining instead of looking at the equation and saying, "Oh, it is an inverse relationship."
Glad to have pointed you over!
People's eyes kind of roll back in their head when they see equations!! That is why editors tell science authors to leave equations out of their books. *face palms*
Seeing the math makes things easier (in my opinion). You can spend a paragraph of words and explaining instead of looking at the equation and saying, "Oh, it is an inverse relationship."
Glad to have pointed you over!
originally posted by: TEOTWAWKIAIFF
a reply to: Groot
People's eyes kind of roll back in their head when they see equations!! That is why editors tell science authors to leave equations out of their books. *face palms*
Seeing the math makes things easier (in my opinion). You can spend a paragraph of words and explaining instead of looking at the equation and saying, "Oh, it is an inverse relationship."
Glad to have pointed you over!
I remember my days with equations and calculus and such.
But, that was along time ago. I still use some of it and it always interests me when I see it , especially in movies.
Gets the old clock moving again.
Keep it up , and thank you !
a reply to: Groot



I like doing the derivation in terms of p! There is almost something magical about going from infinite addition to infinite multiplication of subtraction!
It is here that I stop. I have done nothing more than shown how the Euler Product is used in restating the Riemann's Zeta function. You can find it in advanced undergrad math texts. Mathematicians find all the "1/x" stuff rather ugly and tend to clean it up as seen in the same first term below,
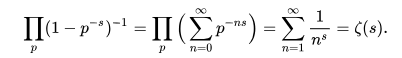
But I have figured something out because it is ugly! Beauty being in the eye of the beholder and such. What you are seeing is screen shots from a PDF I created in word when I was bored. I figured it was a good idea to tag the thing before sharing so what better than some old screen shot from ATS!
I may post the rest but who knows? I may get hit by a bus or something. It is the way life goes.



I like doing the derivation in terms of p! There is almost something magical about going from infinite addition to infinite multiplication of subtraction!
It is here that I stop. I have done nothing more than shown how the Euler Product is used in restating the Riemann's Zeta function. You can find it in advanced undergrad math texts. Mathematicians find all the "1/x" stuff rather ugly and tend to clean it up as seen in the same first term below,
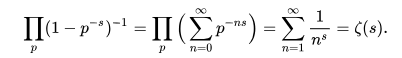
But I have figured something out because it is ugly! Beauty being in the eye of the beholder and such. What you are seeing is screen shots from a PDF I created in word when I was bored. I figured it was a good idea to tag the thing before sharing so what better than some old screen shot from ATS!
I may post the rest but who knows? I may get hit by a bus or something. It is the way life goes.

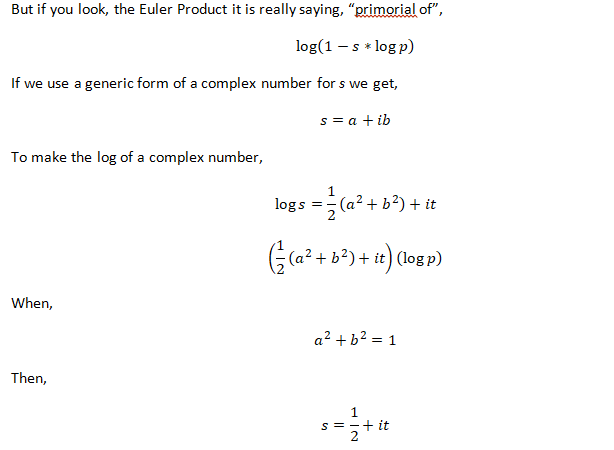

There it is! The final observation I made after deriving the Euler Product.
For those interested, there is a really cool explanation, with examples and "test questions" (the only real way to figure out math is to work with it, make mistakes, have that "Aha!" moment. Also trying to explain math helps one understand math--it certainly helped me!), involving imaginary numbers (the first half. The second explains the "quaternions" which mashes up against reality as it explains 3-D space).
Quantamagazine.org - The (Imaginary) Numbers at the Edge of Reality.
Plus that is a really cool title!
ETA: Quaternions involve the fine structure constant and the "proof" of RH relies on it! It all comes full circle!
edit on 26-10-2018 by
TEOTWAWKIAIFF because: add comment
As Atiyah notes, in some sense α is a fundamental dimensionless numerical quantity like e or π. As such it is tempting to try to “derive” its value from some deeper principles. Arthur Eddington famously tried to derive exactly 1/137, but failed; Atiyah cites him approvingly.
But to a modern physicist, this seems like a misguided quest. First, because renormalization theory teaches us that α isn’t really a number at all; it’s a function. In particular, it’s a function of the total amount of momentum involved in the interaction you are considering. Essentially, the strength of electromagnetism is slightly different for processes happening at different energies. Atiyah isn’t even trying to derive a function, just a number.
Sean Carroll (blog), preposterousuniverse.com - Atiyah and the Fine-Structure Constant.
Looks like Atiyah is on shaky grounds with his proof and the use of the Todd function.
I think the easier route is the unit circle in the complex plane.
PS - I may have a "magic happens" in the middle pane above. If so, sorry! Just having fun with equations and caffeine!
Adding link to read later (arxiv.org): The Fine Structure Constant And Numerical Alchemy.
a reply to: Myself
quantamagazine.org, Oct. 31, 2018 - Without a Proof, Mathematicians Wonder How Much Evidence Is Enough.
The article is on a totally different topic but it explains a unit circle! There is even a graph.
I was thinking about the unit circle in the complex plane and RZ. If it was a larger circle (where: a^2 + b^2 > 1) then it would just be a multiple of RZ.
Here is a nice u-tube vid to help visualize a complex function (and RZ).
eta: It really gets going around 5-7 minutes where it shows input space mapped to function output space using complex numbers
Point to Point
If you’re handed an equation, you can graph its solutions and produce a curve. Mathematicians want to know how many of these solutions are rational numbers — values that can be expressed as a ratio of two integers (such as 1/2, −3, or 4483/929).
Rational solutions are hard to find systematically, but mathematicians have techniques that work under some circumstances. Say you have the equation x^2 + y^2 = 1. The graph of the solutions to this equation form a circle. To find all the rational points on that circle, start with one particular rational solution — say, the point on the circle where x is 1 and y is 0. Then draw a line through that point that intersects the circle at one other point. So long as the slope of your line is rational, the second point of intersection will also be a rational solution. Through the line-drawing procedure, you’ve parlayed one rational solution into two.
quantamagazine.org, Oct. 31, 2018 - Without a Proof, Mathematicians Wonder How Much Evidence Is Enough.
The article is on a totally different topic but it explains a unit circle! There is even a graph.
I was thinking about the unit circle in the complex plane and RZ. If it was a larger circle (where: a^2 + b^2 > 1) then it would just be a multiple of RZ.
Here is a nice u-tube vid to help visualize a complex function (and RZ).
eta: It really gets going around 5-7 minutes where it shows input space mapped to function output space using complex numbers
edit on 1-11-2018 by TEOTWAWKIAIFF because: formatting
edit on 1-11-2018 by TEOTWAWKIAIFF because: clarity
Well, the weird trails life takes us...
NYTimes - Michael Atiyah, Mathematician in Newton’s Footsteps, Dies at 89.
I think most will respect the work he did and not judge him on his wayward RH solution (still in doubt).
Great mathematician. Tied physics to abstract math and showed some precient ideas.
I think RH will fall back into the “unsolved” category after a respectful amount of time.
RIP, Sir Atiyah.
NYTimes - Michael Atiyah, Mathematician in Newton’s Footsteps, Dies at 89.
I think most will respect the work he did and not judge him on his wayward RH solution (still in doubt).
Great mathematician. Tied physics to abstract math and showed some precient ideas.
I think RH will fall back into the “unsolved” category after a respectful amount of time.
RIP, Sir Atiyah.
new topics
-
A Warning to America: 25 Ways the US is Being Destroyed
New World Order: 3 hours ago -
President BIDEN's FBI Raided Donald Trump's Florida Home for OBAMA-NORTH KOREA Documents.
Political Conspiracies: 8 hours ago -
Maestro Benedetto
Literature: 10 hours ago -
Is AI Better Than the Hollywood Elite?
Movies: 10 hours ago
top topics
-
President BIDEN's FBI Raided Donald Trump's Florida Home for OBAMA-NORTH KOREA Documents.
Political Conspiracies: 8 hours ago, 28 flags -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues: 15 hours ago, 8 flags -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest: 17 hours ago, 7 flags -
Las Vegas UFO Spotting Teen Traumatized by Demon Creature in Backyard
Aliens and UFOs: 14 hours ago, 6 flags -
A Warning to America: 25 Ways the US is Being Destroyed
New World Order: 3 hours ago, 6 flags -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News: 17 hours ago, 5 flags -
2024 Pigeon Forge Rod Run - On the Strip (Video made for you)
Automotive Discussion: 14 hours ago, 4 flags -
Is AI Better Than the Hollywood Elite?
Movies: 10 hours ago, 3 flags -
The functionality of boldening and italics is clunky and no post char limit warning?
ATS Freshman's Forum: 16 hours ago, 1 flags -
Maestro Benedetto
Literature: 10 hours ago, 1 flags
active topics
-
Victoria government has cancelled the commmonwealth games, no money.
Regional Politics • 3 • : nazaretalazareta -
A Warning to America: 25 Ways the US is Being Destroyed
New World Order • 2 • : Disgusted123 -
President BIDEN's FBI Raided Donald Trump's Florida Home for OBAMA-NORTH KOREA Documents.
Political Conspiracies • 19 • : ADVISOR -
When an Angel gets his or her wings
Religion, Faith, And Theology • 22 • : AcrobaticDreams1 -
King Charles 111 Diagnosed with Cancer
Mainstream News • 321 • : FlyersFan -
Is there a hole at the North Pole?
ATS Skunk Works • 41 • : burritocat -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest • 16 • : FlyersFan -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues • 33 • : FlyersFan -
Weinstein's conviction overturned
Mainstream News • 24 • : burritocat -
-@TH3WH17ERABB17- -Q- ---TIME TO SHOW THE WORLD--- -Part- --44--
Dissecting Disinformation • 690 • : burritocat
11
