It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
5
share:
Science!
i am an ignoramus so you go ahead and figger her out.
But as far as i can reckon there's Copenhagen View which states the position of a subatomic particle can only be expressed as a probability vs Bohmian mechanics which say all particles are in definite positions .
So anywho...
A team of physicists have devised an experiment based on the famous double slit experiment and using entangled photons as a probe/sensor claim they have proved certain improbable behaviors of Bohmian mechanics, such as particles taking crazy improbable paths, and entangled pairs mimicking faster than light effects
i am an ignoramus so you go ahead and figger her out.
But as far as i can reckon there's Copenhagen View which states the position of a subatomic particle can only be expressed as a probability vs Bohmian mechanics which say all particles are in definite positions .
So anywho...
A team of physicists have devised an experiment based on the famous double slit experiment and using entangled photons as a probe/sensor claim they have proved certain improbable behaviors of Bohmian mechanics, such as particles taking crazy improbable paths, and entangled pairs mimicking faster than light effects
OF THE MANY counterintuitive features of quantum mechanics, perhaps the most challenging to our notions of common sense is that particles do not have locations until they are observed. This is exactly what the standard view of quantum mechanics, often called the Copenhagen interpretation, asks us to believe. Instead of the clear-cut positions and movements of Newtonian physics, we have a cloud of probabilities described by a mathematical structure known as a wave function. The wave function, meanwhile, evolves over time, its evolution governed by precise rules codified in something called the Schrödinger equation. The mathematics are clear enough; the actual whereabouts of particles, less so. Until a particle is observed, an act that causes the wave function to “collapse,” we can say nothing about its location.
Bohmian mechanics was worked out by Louis de Broglie in 1927 and again, independently, by David Bohm in 1952, who developed it further until his death in 1992. (It’s also sometimes called the de Broglie–Bohm theory.) As with the Copenhagen view, there’s a wave function governed by the Schrödinger equation. In addition, every particle has an actual, definite location, even when it’s not being observed. Changes in the positions of the particles are given by another equation, known as the “pilot wave” equation (or “guiding equation”). The theory is fully deterministic; if you know the initial state of a system, and you’ve got the wave function, you can calculate where each particle will end up. That may sound like a throwback to classical mechanics, but there’s a crucial difference. Classical mechanics is purely “local”—stuff can affect other stuff only if it is adjacent to it (or via the influence of some kind of field, like an electric field, which can send impulses no faster than the speed of light). Quantum mechanics, in contrast, is inherently nonlocal. The best-known example of a nonlocal effect—one that Einstein himself considered, back in the 1930s—is when a pair of particles are connected in such a way that a measurement of one particle appears to affect the state of another, distant particle. The idea was ridiculed by Einstein as “spooky action at a distance.” But hundreds of experiments, beginning in the 1980s, have confirmed that this spooky action is a very real characteristic of our universe.
“The universe seems to like talking to itself faster than the speed of light,” said Steinberg. “I could understand a universe where nothing can go faster than light, but a universe where the internal workings operate faster than light, and yet we’re forbidden from ever making use of that at the macroscopic level—it’s very hard to understand.
edit on 22-5-2016 by dashen because: (no reason given)
a reply to: dashen
One of my favorites . The double slit experiment.Also , not only Schrödinger' equation but the old Schrödinger's cat example. The Copenhagen theorem is the only one that can explain certain "absurdities" in Quantum Physics and Mechanics
You reckon well.
Peace
One of my favorites . The double slit experiment.Also , not only Schrödinger' equation but the old Schrödinger's cat example. The Copenhagen theorem is the only one that can explain certain "absurdities" in Quantum Physics and Mechanics
But as far as i can reckon there's Copenhagen View which states the position of a subatomic particle can only be expressed as a probability
You reckon well.
Peace
As far as I know (though I could be wrong) weak measurements like this don't contradict QM, so this isn't proof of dBB, it just shows that its not
ruled out. dBB is entirely equivalent to QM when the particles are in equilibrium, and I don't think we have the technology to test if non-equilibrium
states exist yet.
What I have against dBB is that once you get to quantum field theory, the math of dBB becomes horrible, and all the intuition it boasts about like particles behaving almost classically goes out the window. QFTs math is extreme neat in comparison.
What I have against dBB is that once you get to quantum field theory, the math of dBB becomes horrible, and all the intuition it boasts about like particles behaving almost classically goes out the window. QFTs math is extreme neat in comparison.
So what does this mean for certain theories such as parallel worlds?
What does this mean for super-position and the uncertainty principle?
What does this mean for super-position and the uncertainty principle?
a reply to: dashen
Analogous to a computer?
Internals run @ GHz/MHz range, but the output is limited (for us) to daHz for screen refresh, or kHz for sound.
And NO I am not suggesting anything related to living in holograms or matrices.... not yet anyways...
“The universe seems to like talking to itself faster than the speed of light,” said Steinberg. “I could understand a universe where nothing can go faster than light, but a universe where the internal workings operate faster than light, and yet we’re forbidden from ever making use of that at the macroscopic level—it’s very hard to understand.
Analogous to a computer?
Internals run @ GHz/MHz range, but the output is limited (for us) to daHz for screen refresh, or kHz for sound.
And NO I am not suggesting anything related to living in holograms or matrices.... not yet anyways...
That's not exactly what Bohmian mechanics proposes as the article explains, and it also claims that most rejections of Bohmian mechanics are based on misunderstandings of the Bohmian mechanics model.
originally posted by: dashen
But as far as i can reckon there's Copenhagen View which states the position of a subatomic particle can only be expressed as a probability vs Bohmian mechanics which say all particles are in definite positions .
It's a great article, so thanks for posting it. The experiment provides a little more information so it's an advancement in that respect, but it doesn't seem to prove Bohmian mechanics or resolve anything.
I think Bohmian mechanics has been an option on the table and it still is, even though it's not very popular, some claim because Bohm was a "dirty commie" and people didn't want to be a follower of a "dirty commie".
As for "Overthrowing the Standard View of Quantum Mechanics", the Copenhagen interpretation is taught in textbooks but it's really not as standard as that headline would imply because physicists are divided on how quantum mechanics should be interpreted and most will admit that no interpretation has been conclusively proven to the exclusion of others. So it's still an open question but as with each new novel experiment, now we know slightly more than we did before.
edit on 2016522 by Arbitrageur because: clarification
a reply to: Arbitrageur
Would you mind clarifying that it's in the article that states bohmian Mechanics Contains the possibility ofTrans Universal Pilot waves?
Does that mean a photon could potentially shoot offa Across the Universe if the amplitude of the wave was large enough?
Would you mind clarifying that it's in the article that states bohmian Mechanics Contains the possibility ofTrans Universal Pilot waves?
Does that mean a photon could potentially shoot offa Across the Universe if the amplitude of the wave was large enough?
a reply to: dashen
As the article said physicists have misunderstood Bohmian mechanics and they have an extensive background in physics that usually spans over a decade so the chances it can be explained satisfactorily in a forum post are nil, but here's a citation from your source that you can consider:
As the article said physicists have misunderstood Bohmian mechanics and they have an extensive background in physics that usually spans over a decade so the chances it can be explained satisfactorily in a forum post are nil, but here's a citation from your source that you can consider:
In the Bohmian view, nonlocality is even more conspicuous. The trajectory of any one particle depends on what all the other particles described by the same wave function are doing. And, critically, the wave function has no geographic limits; it might, in principle, span the entire universe. Which means that the universe is weirdly interdependent, even across vast stretches of space. The wave function “combines—or binds—distant particles into a single irreducible reality,” as Sheldon Goldstein, a mathematician and physicist at Rutgers University, has written.
Photons travel at the speed of light so they generally don't travel across the universe any faster than that (they can appear to travel across short distances in a lab faster in quantum tunneling experiments). What they can do is interact with other photons in other parts of the universe faster than the speed of light, or at least observations of of distant entangled photons are correlated, because another model mentioned in your source, "Many worlds" says there's no interaction and that observation is local, and that experimental results are explained because we don't know which universe we are going to be observing, which gives the appearance of non-locality under other interpretations such as DeBroglie-Bohm and Copenhagen.
Does that mean a photon could potentially shoot offa Across the Universe if the amplitude of the wave was large enough?
edit on 2016522 by Arbitrageur because: clarification
self edit, misunderstood OP
edit on 5/22/2016 by bigfatfurrytexan because: (no reason given)
a reply to: dashen
I love reading about this stuff. No expert myself, but it is still fascinating. There is so much we don't know bout how things work, and there are so many possibilities to consider when we look at how things actually seem to behave.
Long distance effects are one of these. Such things could, perhaps, explain some phenomena that we cannot understand, such as "psychic" knowledge, or cases of someone knowing something about a distant loved one. Perhaps, in those cases, some particles in the people re connected, as the tests describe, and thus information can be somehow transmitted.
More than one case in my own family of someone knowing something about a family member, without being told. Perhaps this is why.
I love reading about this stuff. No expert myself, but it is still fascinating. There is so much we don't know bout how things work, and there are so many possibilities to consider when we look at how things actually seem to behave.
Long distance effects are one of these. Such things could, perhaps, explain some phenomena that we cannot understand, such as "psychic" knowledge, or cases of someone knowing something about a distant loved one. Perhaps, in those cases, some particles in the people re connected, as the tests describe, and thus information can be somehow transmitted.
More than one case in my own family of someone knowing something about a family member, without being told. Perhaps this is why.
a reply to: Arbitrageur
Why do people prefer to accept 'many worlds' (for which there is no evidence and is philosophically insane) and not the proven experimental facts of quantum-level non-locality?
We should really start believing what the experiments keep on telling us time and time again:
a) collapse happens early and often and is a real phenomenon
b) something in QM is non-local and makes for strange experimental consequences
c) but we can't transmit human-useful macroscopic information non-locally.
Why do people prefer to accept 'many worlds' (for which there is no evidence and is philosophically insane) and not the proven experimental facts of quantum-level non-locality?
We should really start believing what the experiments keep on telling us time and time again:
a) collapse happens early and often and is a real phenomenon
b) something in QM is non-local and makes for strange experimental consequences
c) but we can't transmit human-useful macroscopic information non-locally.
a reply to: Arbitrageur
Why do people prefer to accept 'many worlds' (for which there is no evidence and is philosophically insane) and not the proven experimental facts of quantum-level non-locality?
We should really start believing what the experiments keep on telling us time and time again:
a) collapse happens early and often and is a real phenomenon. There are no half-dead cats.
b) something in QM is non-local and makes for strange experimental consequences
c) but we can't transmit human-useful macroscopic information non-locally.
Why do people prefer to accept 'many worlds' (for which there is no evidence and is philosophically insane) and not the proven experimental facts of quantum-level non-locality?
We should really start believing what the experiments keep on telling us time and time again:
a) collapse happens early and often and is a real phenomenon. There are no half-dead cats.
b) something in QM is non-local and makes for strange experimental consequences
c) but we can't transmit human-useful macroscopic information non-locally.
edit on 23-5-2016 by mbkennel because: (no reason given)
a reply to: mbkennel
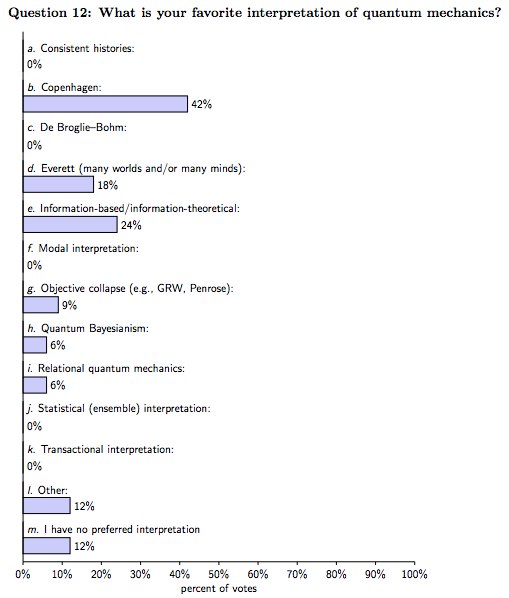
I don't like many worlds interpretation either, but you're right that in this survey of physicists it was vastly preferred to DeBroglie-Bohm where Many world got 18% and DeBroglie-Bohm got 0%:
www.preposterousuniverse.com...
I mentioned one hypothesis I read elsewhere about why the DeBroglie-Bohm interpretation was so unpopular, but I don't understand the popularity of Many Worlds; it would make more sense to me if those two percentages were inverted. If I had to guess why people believe it, maybe it's because some people find it easier to give up a "single universe" than to give up "locality"? While I don't like many worlds and think it's very likely wrong, I don't know how to prove it's wrong and so until we can prove an interpretation correct it's still in the running even if it should be assigned a very low probability of being correct.
Regarding your points a-c, I think Many Worlds agrees with a and c. Regarding point b, Sean Carroll would say it's either non-local, or it's local and multiple universes make it appear non-local. While the multiple universes idea is philosophically not pleasing, as far as I can tell the evidence doesn't prove Carroll is wrong, but you and I both doubt he is right, and he admits he might be wrong and would migrate to another interpretation if it really could be proven by experiment.
I don't like many worlds interpretation either, but you're right that in this survey of physicists it was vastly preferred to DeBroglie-Bohm where Many world got 18% and DeBroglie-Bohm got 0%:
www.preposterousuniverse.com...
I mentioned one hypothesis I read elsewhere about why the DeBroglie-Bohm interpretation was so unpopular, but I don't understand the popularity of Many Worlds; it would make more sense to me if those two percentages were inverted. If I had to guess why people believe it, maybe it's because some people find it easier to give up a "single universe" than to give up "locality"? While I don't like many worlds and think it's very likely wrong, I don't know how to prove it's wrong and so until we can prove an interpretation correct it's still in the running even if it should be assigned a very low probability of being correct.
Regarding your points a-c, I think Many Worlds agrees with a and c. Regarding point b, Sean Carroll would say it's either non-local, or it's local and multiple universes make it appear non-local. While the multiple universes idea is philosophically not pleasing, as far as I can tell the evidence doesn't prove Carroll is wrong, but you and I both doubt he is right, and he admits he might be wrong and would migrate to another interpretation if it really could be proven by experiment.
edit on 2016523 by Arbitrageur because: clarification
I rather like the quote in the article from Einstein:
That is exactly my feeling on Bohmian mechanics. I think in order to accept the pilot wave theory you need to ignore everything about quantum mechanics that indicates truly random events can occur at the quantum scale. Bohmian mechanics and the Many Worlds interpretation are both designed to eliminate that randomness and replace it with some sort of deterministic system. Bohmian mechanics does it by saying there must be some "hidden variables" which we cannot measure (aka the pilot wave) and there really isn't any random process occurring, it just looks random without being able to see the hidden variables. The Many Worlds interpretation does it by saying that actually the particle took every possible path, it didn't randomly choose a path, we just see the outcome in our reality (although alternative versions of our self would see other outcomes).
In my opinion these are both cheap deterministic solutions. There are many reasons to doubt Bohmian mechanics and that article only mentions a few of them. It's much harder to discredit the Many Worlds interpretation because it seems to predict exactly the same experimental results as the Copenhagen interpretation, unless we can some how detect the existence of parallel universes or alternative time lines. But I think the implications of the different interpretations matters even if we cannot confirm which is true. For example if every possible outcome is realized in some universe, there are worlds where I'm a mass murderer and other worlds where I'm a super hero, it makes my choices seem irrelevant and just doesn't strike me as a rational view of reality.
If Bohmian mechanics is true then every choice I will ever make was determined at the start of time and everything I will every do is the result of some ultimate wave equation, again making my choices seem completely meaningless. Personally, I tend to lean towards the Copenhagen interpretation or variants of it because it's the only one which doesn't seem to strip me of any sense of having free will, and if one is willing to accept the idea that nature can be non-deterministic then it feels like the best fit for all the evidence. I think that many people simply cannot accept the notion that events can occur without a clear cause, so the Copenhagen interpretation seems like nonsense to them. I like this quote from Tony Padilla, it sums up my feelings on this issue well:
Have you noticed that Bohm believes (as de Broglie did, by the way, 25 years ago) that he is able to interpret the quantum theory in deterministic terms? That way seems too cheap to me. But you, of course, can judge this better than I.
That is exactly my feeling on Bohmian mechanics. I think in order to accept the pilot wave theory you need to ignore everything about quantum mechanics that indicates truly random events can occur at the quantum scale. Bohmian mechanics and the Many Worlds interpretation are both designed to eliminate that randomness and replace it with some sort of deterministic system. Bohmian mechanics does it by saying there must be some "hidden variables" which we cannot measure (aka the pilot wave) and there really isn't any random process occurring, it just looks random without being able to see the hidden variables. The Many Worlds interpretation does it by saying that actually the particle took every possible path, it didn't randomly choose a path, we just see the outcome in our reality (although alternative versions of our self would see other outcomes).
In my opinion these are both cheap deterministic solutions. There are many reasons to doubt Bohmian mechanics and that article only mentions a few of them. It's much harder to discredit the Many Worlds interpretation because it seems to predict exactly the same experimental results as the Copenhagen interpretation, unless we can some how detect the existence of parallel universes or alternative time lines. But I think the implications of the different interpretations matters even if we cannot confirm which is true. For example if every possible outcome is realized in some universe, there are worlds where I'm a mass murderer and other worlds where I'm a super hero, it makes my choices seem irrelevant and just doesn't strike me as a rational view of reality.
If Bohmian mechanics is true then every choice I will ever make was determined at the start of time and everything I will every do is the result of some ultimate wave equation, again making my choices seem completely meaningless. Personally, I tend to lean towards the Copenhagen interpretation or variants of it because it's the only one which doesn't seem to strip me of any sense of having free will, and if one is willing to accept the idea that nature can be non-deterministic then it feels like the best fit for all the evidence. I think that many people simply cannot accept the notion that events can occur without a clear cause, so the Copenhagen interpretation seems like nonsense to them. I like this quote from Tony Padilla, it sums up my feelings on this issue well:
So if we're ok with wave-function collapse because we understand it through this decoherence, what's wrong with the idea that nature is probabilistic? Why do we have to have that every possibility is realized? Quantum mechanics is probabilistic, that's the way nature is, and just because our classical intuition tells us that we enjoy a deterministic existence, that doesn't mean quantum mechanics has to behave like that, it doesn't mean nature has to behave like that, it just means day to day that's how it seems to behave, but truly it's probabilistic. And that's fine, ok. It doesn't mean that every possibility has to be realized.
a reply to: Arbitrageur
My vote is for "objective collapse".
And what is "cheap" about determinism? We now know, which was not really appreciated in 1930's by physicists, that deterministic systems, in particular with large particle numbers, can give results indistinguishable from 'fundamentally random' ones in virtually all experimentally accessible situations.
Here's how I think about it. Consider other unknowns like dark energy and dark matter. Physicists don't go about saying "you're thinking of the problem wrong, you just have to change your philosophy, and accept all these weird ideas". That would be a "you're holding the phone wrong" attitude (there was a RF reception problem on early iPhone 4's which Jobs didn't accept at first and told the complainers to hold their phones differently).
Instead, they adopt the "interpretation" of physics which has stood the test of time since the days of Newton: there is an objective reality and with sufficiently diligent experimentation and theory we will discover the underlying principles and dynamics which best and most economically explain the observable facts. There is no "interpretation" BS needed in any other part of physics.
I take Einstein's side---halfway. Quantum mechanics (as believed by Copenhagen) is correct (experimentally replicable) but incomplete. Full locality is not true, but every other mystery goes away with nonlinearity and objective collapse and we should not be afraid to suppose new physics or incorrectly understood conventional physics as the underlying explanation instead of letting the ideologues tell us that we are Physicsing Wrong.
My vote is for "objective collapse".
And what is "cheap" about determinism? We now know, which was not really appreciated in 1930's by physicists, that deterministic systems, in particular with large particle numbers, can give results indistinguishable from 'fundamentally random' ones in virtually all experimentally accessible situations.
Here's how I think about it. Consider other unknowns like dark energy and dark matter. Physicists don't go about saying "you're thinking of the problem wrong, you just have to change your philosophy, and accept all these weird ideas". That would be a "you're holding the phone wrong" attitude (there was a RF reception problem on early iPhone 4's which Jobs didn't accept at first and told the complainers to hold their phones differently).
Instead, they adopt the "interpretation" of physics which has stood the test of time since the days of Newton: there is an objective reality and with sufficiently diligent experimentation and theory we will discover the underlying principles and dynamics which best and most economically explain the observable facts. There is no "interpretation" BS needed in any other part of physics.
I take Einstein's side---halfway. Quantum mechanics (as believed by Copenhagen) is correct (experimentally replicable) but incomplete. Full locality is not true, but every other mystery goes away with nonlinearity and objective collapse and we should not be afraid to suppose new physics or incorrectly understood conventional physics as the underlying explanation instead of letting the ideologues tell us that we are Physicsing Wrong.
edit on 24-5-2016 by mbkennel because: (no reason given)
edit on 24-5-2016 by mbkennel because: (no reason given)
The above is as much bull# as it can be. In fact, it may be the definition of bull# one day.
The words used to describe the phenomenon are meaningless and deliberately confusing in order to give rise to extraordinary and impossible ideas.
For example, the phrases "if no observation is made" and "yet if an observer checks to see", along with the 'eye' icon, make the reader thing that when a person views the experiment, its outcome changes.
That couldn't be further from the truth. The observer is a particle detector machine which accepts the particles on one end and outputs other particles out of the other end, towards the slits.
Another example is this: "each electron spreads out like a wave, passes through both slits simultaneously, and interferes with itself to form the bright and dark bands on the detector screen".
Well, that's wrong. If a single electron is fired, a single dot will appear on the detector screen, not a band. A band will appear after a stream of electrons is fired onto the slits.
Which means the whole thing is totally 100% bull#.
There are also other facts to take care into account:
1) if the slits change orientation, the band pattern is changed accordingly. For example, if the slits become horizontal, the bands become horizontal.
If the particles were actually a wave, that wouldn't happen. It is not possible that the orientation of the slits changes also the orientation of the electron wave, because the two are disconnected.
This fact alone says electrons are not waves.
2) if the slits change size, i.e. become a bit wider, then the bands disappear.
If the slits become narrower, more bands appear.
This means the width of the slits affects the number of bands. If the slits are wide enough, the bands disappear.
This again means that the electrons are not a wave! if it was, making the slits a bit wider wouldn't affect the bands, because the wave would still have been wide enough to create the band effect.
This means that the electrons are simply slingshot to certain positions when passing through the slits, due to the slits being narrow enough to not allow an electron to fully pass through it.
When a detector is put in between the electron gun and the slits, the electron is somewhat modified in such a way that it no longer has a problem fitting the slit.
I bet that even with a detector, if the slits are small enough, there will still be an interference pattern in the end.
Quantum mechanics, in contrast, is inherently nonlocal. The best-known example of a nonlocal effect—one that Einstein himself considered, back in the 1930s—is when a pair of particles are connected in such a way that a measurement of one particle appears to affect the state of another, distant particle. The idea was ridiculed by Einstein as “spooky action at a distance.” But hundreds of experiments, beginning in the 1980s, have confirmed that this spooky action is a very real characteristic of our universe.
Even more bull#.
1) If information cannot travel faster than light, then IT IS NOT POSSIBLE TO MEASURE THE CHANGE ON AN ENTANGLED PARTICLE IN RELATION TO ANOTHER ENTANGLED PARTICLE WE HAVE MEASURED. This would allow for superluminal speed of transfer of information.
2) the "hundreds of experiments" mentioned above DO NOT MAKE A DELIBERATE CHANGE TO ONE OF AN ENTANGLED PARTICLE'S ATTRIBUTES LIKE SPIN. THE EXPERIMENTS MEASURE THE EXISTING SPIN OF THE ENTANGLED PARTICLES, which are found to be statistically correlated for if the particles are previously entangled. THEY SUPPOSE THEN THAT THERE IS SOME SORT OF CONNECTION BETWEEN THE PARTICLES, WHICH IS SUPERLUMINAL IN SPEED, BECAUSE THEY HAVE PREVIOUSLY SAID THAT THE PARTICLES DON'T HAVE A DEFINITE SPIN BEFORE THEY ARE MEASURED! which is a totally absurd conclusion, because the initial assumption is bull#!
3) in fact, no experiment has proved that the statistical correlation of the entangled particles' spin is not created at the moment the particles are entangled. It may very well be the case that THE SPINS ARE CORRELATED JUST WHEN THE ENTANGLED PARTICLES ARE CREATED.
4) Bell, in his famous "Bell inequalities" theory, which is the basis of QM, makes the ADHOC ASSUMPTION, IN HIS THOUGHT EXPERIMENT, THAT IF THERE WERE HIDDEN VARIABLES, THE SPIN OF ENTANGLED PARTICLES SHOULD BE LINEARLY CORRELATED TO THE ANGLE THE ENTANGLED PARTICLES ARE FIRED! this is bull#, it's an assumption straight out of his ass.
5) the experiments that 'prove' entanglement don't actually prove anything, because the particles that begin as separated are not the same particles that end up entangled. The descriptions of the experiments read like this: "two electrons are transmitted down two separate paths, they are measured for spin, they have uncorrelated spin, then they are entangled, they are measured again and have correlated spin". Well, the entangled particles are not the same as the particles that were initially fired! they may have the same energy, BUT THEY ARE NOT THE SAME PARTICLES! In fact, the initial particles are destroyed within the process of entanglement, and two new particles are created!!!!
If it's bull then how do you explain the bands forming when the electrons are fired one at a time? Yes if you only look at one electron you only get one dot, but when you do that over and over again the one dots add up to form a band pattern. What's your explanation for the interference pattern if you don't accept the scientific explanation?
originally posted by: masterp
Another example is this: "each electron spreads out like a wave, passes through both slits simultaneously, and interferes with itself to form the bright and dark bands on the detector screen".
Well, that's wrong. If a single electron is fired, a single dot will appear on the detector screen, not a band. A band will appear after a stream of electrons is fired onto the slits.
Which means the whole thing is totally 100% bull#.
a reply to: masterp
This is the most naive interpretation of quantum mechanics possible. The slits don't just happen to jostle around the particle in such a way to create the interference pattern, countless experiments have been done to show the wave function is a real phenomena and the double slit experiment is one of the most basic examples. Other more advanced versions of the experiment such as the delayed choice quantum eraser demonstrates superposition in a much more explicit fashion and also demonstrates much weirder things like non-locality caused by entanglement. Two things seem pretty clear based on all our experimental results: a particle can exist in a state of superposition and entanglement can allow particles to communicate in some way instantaneously over any distance. However all our experiments also tell us that we cannot use that non-locality to send any meaningful information between particles, the delayed choice quantum eraser demonstrates that in a very subtle but interesting way.
My conclusion is that we do live in an objective reality, the moon clearly exists when no one is looking at it, but the particles making up the moon don't necessarily need to have an exact position and they don't need to behave in a deterministic fashion, their position can be smeared out like a wave (eg electron standing waves) and they can decay at random times. However even though I would say reality is objective and observers play no special role, it's also clear that the universe is weird and will use any trick in the book to get things done, so long as that trick can never be used to violate causality or objectivity. Instantaneous communication is fine as long as it never communicates anything which could objectively violate causality. A particle being in a wave state is fine as long as it objectively appears to be a particle when measured. The universe doesn't try to calculate the exact position or motion of every particle with perfect accuracy, it does enough to maintain an objective reality and absolutely nothing more.
This means that the electrons are simply slingshot to certain positions when passing through the slits, due to the slits being narrow enough to not allow an electron to fully pass through it.
When a detector is put in between the electron gun and the slits, the electron is somewhat modified in such a way that it no longer has a problem fitting the slit.
This is the most naive interpretation of quantum mechanics possible. The slits don't just happen to jostle around the particle in such a way to create the interference pattern, countless experiments have been done to show the wave function is a real phenomena and the double slit experiment is one of the most basic examples. Other more advanced versions of the experiment such as the delayed choice quantum eraser demonstrates superposition in a much more explicit fashion and also demonstrates much weirder things like non-locality caused by entanglement. Two things seem pretty clear based on all our experimental results: a particle can exist in a state of superposition and entanglement can allow particles to communicate in some way instantaneously over any distance. However all our experiments also tell us that we cannot use that non-locality to send any meaningful information between particles, the delayed choice quantum eraser demonstrates that in a very subtle but interesting way.
My conclusion is that we do live in an objective reality, the moon clearly exists when no one is looking at it, but the particles making up the moon don't necessarily need to have an exact position and they don't need to behave in a deterministic fashion, their position can be smeared out like a wave (eg electron standing waves) and they can decay at random times. However even though I would say reality is objective and observers play no special role, it's also clear that the universe is weird and will use any trick in the book to get things done, so long as that trick can never be used to violate causality or objectivity. Instantaneous communication is fine as long as it never communicates anything which could objectively violate causality. A particle being in a wave state is fine as long as it objectively appears to be a particle when measured. The universe doesn't try to calculate the exact position or motion of every particle with perfect accuracy, it does enough to maintain an objective reality and absolutely nothing more.
edit on 25/5/2016 by ChaoticOrder because: (no reason given)
new topics
-
BIDEN Admin Begins Planning For January 2025 Transition to a New President - Today is 4.26.2024.
2024 Elections: 45 minutes ago -
Big Storms
Fragile Earth: 2 hours ago -
Where should Trump hold his next rally
2024 Elections: 4 hours ago -
Shocking Number of Voters are Open to Committing Election Fraud
US Political Madness: 5 hours ago -
Gov Kristi Noem Shot and Killed "Less Than Worthless Dog" and a 'Smelly Goat
2024 Elections: 6 hours ago -
Falkville Robot-Man
Aliens and UFOs: 6 hours ago -
James O’Keefe: I have evidence that exposes the CIA, and it’s on camera.
Whistle Blowers and Leaked Documents: 7 hours ago -
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order: 8 hours ago -
Ireland VS Globalists
Social Issues and Civil Unrest: 8 hours ago -
Biden "Happy To Debate Trump"
2024 Elections: 9 hours ago
top topics
-
James O’Keefe: I have evidence that exposes the CIA, and it’s on camera.
Whistle Blowers and Leaked Documents: 7 hours ago, 14 flags -
Blast from the past: ATS Review Podcast, 2006: With All Three Amigos
Member PODcasts: 11 hours ago, 13 flags -
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order: 8 hours ago, 12 flags -
Biden "Happy To Debate Trump"
2024 Elections: 9 hours ago, 12 flags -
Mike Pinder The Moody Blues R.I.P.
Music: 11 hours ago, 8 flags -
What is the white pill?
Philosophy and Metaphysics: 10 hours ago, 6 flags -
Shocking Number of Voters are Open to Committing Election Fraud
US Political Madness: 5 hours ago, 6 flags -
RAAF airbase in Roswell, New Mexico is on fire
Aliens and UFOs: 9 hours ago, 5 flags -
Ireland VS Globalists
Social Issues and Civil Unrest: 8 hours ago, 5 flags -
Where should Trump hold his next rally
2024 Elections: 4 hours ago, 5 flags
active topics
-
Putin, Russia and the Great Architects of the Universe
ATS Skunk Works • 28 • : lostgirl -
Where should Trump hold his next rally
2024 Elections • 17 • : Zanti Misfit -
Gov Kristi Noem Shot and Killed "Less Than Worthless Dog" and a 'Smelly Goat
2024 Elections • 40 • : AwakeNotWoke -
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest • 14 • : TheWoker -
Australian PM says the quiet part out loud - "free speech is a threat to democratic dicourse"...?!
New World Order • 5 • : Zanti Misfit -
BIDEN Admin Begins Planning For January 2025 Transition to a New President - Today is 4.26.2024.
2024 Elections • 4 • : Zanti Misfit -
James O’Keefe: I have evidence that exposes the CIA, and it’s on camera.
Whistle Blowers and Leaked Documents • 11 • : Zanti Misfit -
"We're All Hamas" Heard at Columbia University Protests
Social Issues and Civil Unrest • 296 • : SchrodingersRat -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media • 313 • : cherokeetroy -
Las Vegas UFO Spotting Teen Traumatized by Demon Creature in Backyard
Aliens and UFOs • 18 • : TheMisguidedAngel
5