Why Pi = 3.141 .. instead of 3.144?

reply to post by JackTheTripper


Here's another which points to wolframalpha

Originally posted by JackTheTripper

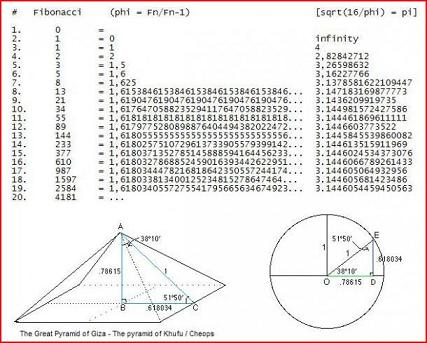
4 cos(pi / 4) = 2.82842712

sqrt(10) = 3.16227766

edit on 10-12-2011 by JackTheTripper because: (no reason given)

Hi JTR,

I have been studying your math and all of the background resources you have provided on the derivation of a fundamental relationship between Phi and Pi. Firstly I commend you on your efforts and probably one of the only few who have come to this thread and actually understood it ... I have a PhD in Physics and Maths, have launched a few communications satellites, and have studied metaphysics and am open to new knowledge that sets mainstream science back on a more fundamentally accurate path.

It too me quite a while to independently derive your Pi Phi formula, but I finally succeeded and reproduced the spreadsheet calculations you supplied in the original 2011 post quoted here. I would love to believe the accuracy of your discovery as it offers scope for improved engineering of systems requiring synchronous high speed rotational operations, etc ...

However, I get hung up on one specific point:

The value of 16 in your formula ( pi = sqrt(16/PHI) ) is derived from some reasonable (but not fundamental) geometric arguments and some very approximate measurements of the dimensions of the Great Pyramid.
If the measurements are only a fraction of a percent out, the value of 16 cannot be taken as gospel, and one has to fall back on the argument that the geometric argument of expansion to a 16 square is reasonably valid.

YOu get the current scientific value of Pi (3.14159265.....) by using the Phi-Pi relation with a value of 15.96935537648 rather than 16 in the equation, which is only a small difference from the formula you propose, and not out of order in terms of the inaccuracies inherent in the Giza dimensional measurement accuracies.

Therefore, if all we have to fall back on is the 16 square geometric principle, I am afraid that i would not stake my reputation and indeed my life on the accuracy of the formula as you have presented it.

I still have an open mind though and would like to see you prove in more depth why the value of 16 is fundamentally accurate, beyond any shadow of a doubt. If you are correct, this is significant for both engineering and science.

However, I am sitting on the fence at the moment and cannot be swayed to your side until further unrefutable evidence, to the required level of precision and confidence, and/or other arguments that have holistic integrity can be put forward.

I would love to discuss what other facts and justification you can put forward and congratulate you in advance that you can meet the challenge.

Many Thanks,
holiweb.

holiweb

Originally posted by JackTheTripper

4 cos(pi / 4) = 2.82842712

sqrt(10) = 3.16227766

edit on 10-12-2011 by JackTheTripper because: (no reason given)

Hi JTR,

I have been studying your math and all of the background resources you have provided on the derivation of a fundamental relationship between Phi and Pi. Firstly I commend you on your efforts and probably one of the only few who have come to this thread and actually understood it ... I have a PhD in Physics and Maths, have launched a few communications satellites, and have studied metaphysics and am open to new knowledge that sets mainstream science back on a more fundamentally accurate path.

It too me quite a while to independently derive your Pi Phi formula, but I finally succeeded and reproduced the spreadsheet calculations you supplied in the original 2011 post quoted here. I would love to believe the accuracy of your discovery as it offers scope for improved engineering of systems requiring synchronous high speed rotational operations, etc ...

However, I get hung up on one specific point:

The value of 16 in your formula ( pi = sqrt(16/PHI) ) is derived from some reasonable (but not fundamental) geometric arguments and some very approximate measurements of the dimensions of the Great Pyramid.
If the measurements are only a fraction of a percent out, the value of 16 cannot be taken as gospel, and one has to fall back on the argument that the geometric argument of expansion to a 16 square is reasonably valid.

YOu get the current scientific value of Pi (3.14159265.....) by using the Phi-Pi relation with a value of 15.96935537648 rather than 16 in the equation, which is only a small difference from the formula you propose, and not out of order in terms of the inaccuracies inherent in the Giza dimensional measurement accuracies.

Therefore, if all we have to fall back on is the 16 square geometric principle, I am afraid that i would not stake my reputation and indeed my life on the accuracy of the formula as you have presented it.

I still have an open mind though and would like to see you prove in more depth why the value of 16 is fundamentally accurate, beyond any shadow of a doubt. If you are correct, this is significant for both engineering and science.

However, I am sitting on the fence at the moment and cannot be swayed to your side until further unrefutable evidence, to the required level of precision and confidence, and/or other arguments that have holistic integrity can be put forward.

I would love to discuss what other facts and justification you can put forward and congratulate you in advance that you can meet the challenge.

Many Thanks,
holiweb.

Dear Holiweb,

One has to think the circle in 3d - from 2d lattice it seems to be circle but it's actually a spiral.
I get the pi-phi relation to 16 by the formula phi*(4/sqrt(phi))^2. As per www.stefanides.gr... :

Using this value for Pi 4/sqrt (phi) as the small side of an orthogonal triangle , 4 its bigger vertical and its hypotenuse 4/sqrt (phi)*phi , inscribing this triangle in a circle of diameter D equal to the hypotenuse = 16 . THIS IS THE CIRCUMFERENCE OF THE CIRCLE= TO THE SQUARE OF THE BIGGER SIDE 4*4= 16 = TO THE IS SQUARE’S PERIMETER.

Multiplying 4*D = 4*(4/sqrt (phi)*phi) = area of circle = (4/sqrt (phi))*(((4/sqrt(phi)*phi)^2)/4)

So we get this Squaring of the Circle relationship, elaborating on PLATO’S TIMAEUS.

reply to post by JackTheTripper


Pi IS 3.14159....

There is no way out of it.

One has to think the circle in 3d - from 2d lattice it seems to be circle but it's actually a spiral.

Ok then show it. I am not sure if I understand you correctly. Maybe you are thinking of time or hyperdimension or something else.

Elaborate more on the spiral or whatever it is that you are trying to explain?

But PI will always be 3.14159....

Deaf Alien
reply to post by JackTheTripper

 

Pi IS 3.14159....

There is no way out of it.

One has to think the circle in 3d - from 2d lattice it seems to be circle but it's actually a spiral.

Ok then show it. I am not sure if I understand you correctly. Maybe you are thinking of time or hyperdimension or something else.

Elaborate more on the spiral or whatever it is that you are trying to explain?

But PI will always be 3.14159....

Do the math and please try to disproove.

In section 53, of PLATO’S “TIMAEUS”, PLATO speaks about the triangular shapes of the Four Elemental Bodies, of their kinds and their combinations : These Bodies are the Fire (Tetrahedron) the Earth (Cube), the Water (Icosahedron), and the Air (Octahedron). These are bodies and have depth. The depth necessarily, contains the flat surface and the perpendicular to this surface is a side of a triangle and all the triangles are generated by two kinds of orthogonal triangles : the “ISOSCELES” Orthogonal and the “SCALΕΝΕ” Orthogonal. From the two kinds of triangles the “Isosceles” Orthogonal has one nature. (i.e. one rectangular angle and two acute angles of 45 degrees), whereas the “scalene” has infinite (i.e. it has one rectangular angle and two acute angles of variable values having, these two acute angles, the sum of 90 degrees). From these infinite natures we choose one triangle “THE MOST BEAUTIFUL”. Let us choose then, two triangles, which are the basis of constructing the Fire and the other Bodies : One of these two is the “ISOSCELES” orthogonal triangle, the other is the “SCALENE” orthogonal triangle, its hypotenuse having a value equal to the “CUBE” of the value of its horizontal smaller side and having its vertical bigger side the value of the “SQUARE” of its smaller horizontal side. The value of the smaller horizontal side is equal to the square root of the GOLDEN NUMBER, the ratio of the sides is equal, again, to the square root of the GOLDEN NUMBER (geometrical ratio) and the Tangent of the angle between the hypotenuse and the smaller horizontal side is also equal to the SQUARE ROOT of the GOLDEN NUMBER (Θ=51 49-38-15-9-17-19-54-37-26-24-0 degrees). By applying THE PYTHAGOREAN THEOREM, on this triangle we obtain a biquadratic ((fourth order)) equation:

(T**4-T**2-1=0, from, T**6 = T**4+T**2, via Φ**2-Φ-1=0)
from which we obtain the size of the small perpendicular (T) as the Square root of the Golden Number (T=SQR(Φ)).

It is concluded here that by “THE MOST BEAUTIFUL TRIANGLE”, PLATO correlates the four elements (UNIFIED THEORY) through the General Analogies of their sides (Fire, Air, Earth and Water), i.e. Fire/Air is equal to Air/Water is equal to Water/Earth, to T, where T is equal to the SQUARE ROOT of the GOLDEN NUMBER.
T = sqrt ((sqrt(5) + 1)/2)=1.27201965

The values of the sides of this triangle are given by surd numbers, (solution of a fourth degree equation). Reorganizing this triangle, we get another one with the same angle values, which has its bigger vertical side equal to FOUR (4), its smaller horizontal side equal to FOUR divided by the SQUARE ROOT of the GOLDEN NUMBER, and its hypotenuse equal to FOUR multiplied by the SQUARE ROOT of the GOLDEN NUMBER. (Four divided by the SQUARE ROOT of the GOLDEN NUMBER is equal to 3.14460551)

reply to post by JackTheTripper


I am not really understanding you.

Are you saying that 3.14159 IS NOT the ratio of a circle's circumference to it's diameter but 3.14461 instead?

One has to think the circle in 3d - from 2d lattice it seems to be circle but it's actually a spiral.

This makes me think of this. Am I close?

reply to post by JackTheTripper

Do the math and please try to disproove.

disprove what?

reply to post by Deaf Alien


Well, kind of yes, as it relates to poincare disk... like drawing a circle on the surface of a sphere. What does a circle look like if it's circumference C and radius r satisfy the C I have proposed. Anyone with mathematica? the howto is here: mathematica.stackexchange.com...

Alternative geometrical method for determining which Pi is the correct value of Pi 3.141592653589793 Traditional Pi or Golden Pi 3.144605511029693:

Traditional Pi 3.141592653589793 multiplied by 2 is traditional Tau 6.283185307179586.
Golden Pi 3.144605511029693 multiplied by 2 is Golden Tau 6.289211022059386.
Traditional Tau 6.283185307179586 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5729.577951308232523 (reduced to 4 decimal places is 5729).
Alternatively traditional tau 6.283185307179586 says that if a circle has a circumference of 360 then the radius of the circle is 57.295779513082325 (reduced to 4 decimal places is 57.29)
Golden Tau 6.289211022059386 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5724.088422813310602 (reduced to 4 decimal places is 5724).
Alternatively Golden Tau 6.289211022059386 says that if a circle has a circumference of 360 then the radius of the circle is 57.240884228133106 (reduced to 4 decimal places is 57.24)
It is a Geometrical fact that if one 8th of a circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) then the result is the measure for the radius of the circle. 1.27201964951406 is the ratio gained from dividing the second longest length of a Kepler scalene right triangle by the shortest edge length of the Kepler scalene triangle. If the radius of a circle is divided by one 8th of the circle’s circumference then the resulting ratio is the square root of 1.618033988749895 (1.27201964951406).
We can use the Pythagorean theorem to determine which value of Pi is correct out of Traditional Pi 3.141592653589793 or Golden Pi 3.144605511029693: en.wikipedia.org...
So if the circumference of the circle is 360 and one 8th of 360 is 45. So if the shortest edge length of a Kepler right triangle is 45 then according to the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 the hypotenuse of the Kepler right triangle is 72.811529493745275. If the hypotenuse of a Kepler right triangle is divided by the shortest edge length of a Kepler right triangle then the result is the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895. 72.811529493745275 divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 is 45.
72.811529493745275 squared is 5301.518827218538062.
45 squared is 2025.
5301.518827218538062 subtract 2025 = 3276.518827218538062.
The square root of 3276.518827218538062 is 57.24088422813311. (reduced to 4 decimal places is 57.24).

So if the circumference of the circle is 36000 and one 8th of 36000 is 4500. So if the shortest edge length of a Kepler right triangle is 4500 then according to the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 the hypotenuse of the Kepler right triangle is 7281.1529493745275. If the hypotenuse of a Kepler right triangle is divided by the shortest edge length of a Kepler right triangle then the result is the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895. 7281.1529493745275 divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 is 4500.
72.811529493745275 squared is 53015188.272185380623353.
4500 squared is 20250000.
53015188.272185380623353 subtract 20250000 = 32765188.272185380623353.
The square root of 32765188.272185380623353 is 5724.088422813311. (reduced to 4 decimal places is 5724).

a reply to: Deaf Alien

To determine which Pi value is the most accurate and true Pi out of the 2 Pi values included in here Traditional Pi of 3.141592653589793 or Golden Pi of 3.144605511029693: (millimetres or centimetres can be used as the units of measure for this demonstration or any other unit of measure that is suitable)
Computer software based upon computer-aided design can be used to achieve the required task or alternatively a very long ruler if the task is to be achieved physically and also a large beam compass.
Please remember that the radius of a circle is half of a circle’s diameter in measure.

Create 2 Golden ratio rectangles and the longer length of each Golden ratio rectangle must be vertical. The shorter lengths of each Golden ratio rectangle can have 4500 equal units of measure each or alternatively 450 equal units of measure. The circumference of the circle can have 36000 equal units of measure or alternatively 360 equal units of measure. If the circumference of a circle has 36000 equal units of measure then 1 quarter of the circle’s circumference is equal to 9000. If the circumference of a circle has 360 equal units of measure then 1 quarter of the circle’s circumference is 90 equal units of measure. Because 90 is 1 quarter of a circle’s circumference that has 360 equal units of measure and 9000 is 1 quarter of a circle’s circumference that has 36000 units of measure 2 Golden ratio rectangles must be placed next to each other so that the shorter lengths of both of the Golden ratio rectangles can form a double square rectangle with 9000 equal units of measure or 90 equal units of measure because 9000 is 1 quarter of a circle’s circumference that has 36000 equal units of measure and alternatively 90 is 1 quarter of a circle with a circumference of 360 equal units of measure. Please remember that the base centre of the longer length of the double square rectangle that is made from the 2 shorter edges of the 2 Golden ratio rectangles is also the centre of a circle with a circumference of 36000 equal units of measure or alternatively the base centre of the double square rectangle can be the centre of a circle with 360 equal units of measure.
Traditional Pi 3.141592653589793 multiplied by 2 is traditional Tau 6.283185307179586.
Golden Pi 3.144605511029693 multiplied by 2 is Golden Tau 6.289211022059386.
Traditional Tau 6.283185307179586 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5729.577951308232523 (reduced to 4 decimal places is 5729).
Alternatively traditional tau 6.283185307179586 says that if a circle has a circumference of 360 then the radius of the circle is 57.295779513082325 (reduced to 4 decimal places is 57.29)
Golden Tau 6.289211022059386 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5724.088422813310602 (reduced to 4 decimal places is 5724).
Alternatively Golden Tau 6.289211022059386 says that if a circle has a circumference of 360 then the radius of the circle is 57.240884228133106 (reduced to 4 decimal places is 57.24)
From the central base of the 2 golden ratio rectangles that create a double square rectangle with its longest length as 9000 equal units of measure or alternatively the double square rectangle can have base width of 90 equal units of measure.
First mark off 5724 equal units of measure if the width of the double square rectangle has 9000 equal units of measure or alternatively 57.24 equal units of measure if the width of the double square rectangle has 90 equal units of measure.
Second mark off 5729 equal units of measure if the width of the double square rectangle has 9000 equal units of measure.
Alternatively mark off 57.29 equal units of measure only if the width of the double square has 90 equal units of measure.

Next to determine if Traditional Tau or Golden Tau is correct swing the longer length of any of the 2 the Golden rectangles on to the central line that originates from the base centre of the double square rectangle that is made from the 2 shorter lengths of the 2 Golden ratio rectangles and the longer length of any of the 2 Golden rectangles will fall on either 5724 the value of the circle’s radius given by Golden Tau or 5729 the value of the circle’s radius given by traditional Tau, if the width of the double square has 9000 equal units of measure. If the compass arc that has a measure equal to any of the 2 longer outer edges for the 2 Golden rectangles fall upon 5724 then Golden Pi 3.144605511029693 will have to accepted as the real Pi, but If the compass arc that has a measure equal to any of the 2 longer outer edges for the 2 Golden rectangles fall upon 5729 then traditional Pi 3.141592653589793 will have to be accepted as the real Pi.

Alternatively if the width of the double square has 90 equal units of measure then the compass arc that is equal to any of the 2 longer lengths of the outer edges of the 2 Golden rectangles will fall upon 57.24 or either 57.29. If the any of the longer edges for the 2 Golden rectangles fall upon 57.24 then Golden Pi 3.144605511029693 is the real Pi and if any of the longer edges for the 2 Golden rectangles fall upon 57.29 then traditional Pi 3.141592653589793 will have to be accepted as the real Pi.
The result is that the correct value of Pi and Tau is determined by the hypotenuse of a Kepler scalene right triangle that has its shortest edge length equal to 1 half of the double square and also the shorter length of any of the 2 Golden ratio rectangles and the longer length of the double square is equal in measure to 1 quarter of the circle’s circumference. The hypotenuse of the Kepler scalene right triangle must be equal in measure to the longer length of any of the 2 Golden ratio rectangles.
The second longest length of the Kepler scalene right triangle can be equal to the radius of the circle with a circumference of 36000 equal units of measure or alternatively The second longest length of the Kepler scalene right triangle can be equal to the radius of the circle with a circumference of 360 equal units of measure.

Remember that the Kepler scalene triangle must be created from any of the 2 Golden ratio rectangles that has its shorter length equal to half the width of the double square rectangle and the Golden ratio rectangles must also be created from half the width of the double square.
Please remember that if 1 eighth of a circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) the result is the measure for the radius of the circle and if 1 quarter of the circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) the result is the measure for the diameter of the circle.
If 1 quarter of the circle’s circumference is multiplied by the square root of 0.618033988749895 (0.786151377757423) then the result is the larger measure of the circle’s diameter being divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Cosine (72) multiplied by 2 = 0.618033988749895 and the square root of 0.618033988749895 is 0.786151377757423. : en.wikipedia.org...:Kepler_Triangle_Construction.svg

a reply to: Deaf Alien

If a isosceles triangle that is made from 2 Kepler right triangles is inscribed inside of a circle then the 2 lengths of the isosceles triangle that emerge from the base of the isosceles triangle are both equal in measure to 1 quarter of the circle’s circumference and this information help to determine the exact length of a circle’s circumference in relation to a circle’s diameter.
1. The hypotenuse of a Kepler triangle divided by the opposite edge length produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
2. If the diameter of the circle is divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the longer measure of the division of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is equal to the second longest edge length of a Kepler right triangle that has its hypotenuse equal in length to 1 quarter of the circle’s circumference when the Kepler right triangle is created inside of the circle.

3. The shorter measure of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is equal in measure to the shortest edge length of a Kepler right triangle that has its hypotenuse equal in measure to the longer measure for the division of this circle’s diameter into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. So the height of the isosceles triangle that is made from 2 Kepler triangles that is inscribed inside of this circle is equal in measure to the hypotenuse of a Kepler right triangle that has its second longest edge length equal in measure to half the base width of the isosceles triangle that is made from 2 Kepler right triangles that has been inscribed inside of this circle.

4. So according to the Pythagorean theorem if 1 quarter of the circle’s circumference is squared and also 1 quarter of the circle’s circumference is divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and the smaller measure of the circle’s circumference that is divided into the Golden ratio of Cosine (36) multiplied by 2 is squared and then subtracted from the square of 1 quarter of the circumference of the circle and the remainder is applied to square root then the result of all the equations can then be divided into the Golden ratio of Cosine ( 36 ) multiplied by 2 = 1.618033988749895 and the shorter measure of the remainder can be added to the remainder resulting in the exact measure for the diameter of the circle in relation to the circle’s circumference.

(A) 1 quarter of the circle’s circumference divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

(B) The result of dividing 1 quarter of the circle’s circumference into the Golden ratio of Cosine (36) multiplied by = 1.618033988749895 multiplied by the square root of 1.618033988749895 (1.27201964951406) results in the second longest edge length of a Kepler triangle that is half of a isosceles triangle created inside of the circle that has its 2 slanted lengths equal to 1 quarter of the circle’s circumference.

(C) The height of the isosceles triangle that has its 2 slanted edge lengths equal to 1 quarter of the circle’s circumference divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the longer measure of the height of the isosceles triangle that has its 2 slanted lengths equal to 1 quarter of the circle’s circumference is divided into the Golden ratio of Cosine (36) by 2 = 1.618033988749895 is added to the second longest edge length of the Kepler right triangle that both equal to the height of this isosceles triangle and is half of this isosceles triangle resulting in the right measure for the diameter of the circle in relation to the circumference of the circle.




So if the isosceles triangle that is inscribed inside of this circle is divided into 2 Kepler right triangles and only 1 of the Kepler right triangles that is half of the isosceles triangle has the Pythagorean theorem applied to it plus the second longest edge length of the Kepler right triangle that is half of the isosceles triangle that has been inscribed inside of this circle is divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter measure of the second longest length of the Kepler right triangle divided into the Golden ratio is added to the second longest edge length of the Kepler right triangle then the correct measure for the length of the circle’s diameter in relation to the circumference of the circle can be known. If the measure for the circumference of a circle is divided by the diameter of the circle the resulting ratio is Pi.

“How to determine the exact circumference of a circle when only the length of the circle’s diameter is known and also further knowledge on how to gain the correct value of Pi”:
1. Divide the diameter of the circle into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter length of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 must then be divided by the square root of 1.618033988749895 (1.27201964951406).

2. The result of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and then be divided by the square root of 1.618033988749895 (1.27201964951406) must now be divided by Cosine (51.82729237298776) resulting in 1 quarter of the circle’s circumference.

Alternatively 1 quarter of a circle’s circumference can be known if only the diameter for circle is known by dividing the diameter of the circle into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and the shorter length of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 must then be squared according to the Pythagorean theorem. Also The result of the circle’s diameter divided into the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 and then be divided by the square root of 1.618033988749895 (1.27201964951406) must now be squared according to the Pythagorean theorem. The combination of both the greater length of the circle’s diameter being divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then the result of the greater length of the division of the circle’s diameter into the Golden ratio of Cosine (36) being divided by the square root of 1.618033988749895 (1.27201964951406) squared according to the Pythagorean theorem and then applied to square root can also reveal the measure for 1 quarter of the circle’s diameter when the circumference of the circle is not yet known and only the measure for the diameter of the circle is known.

3. Now that the measure for 1 quarter of the circle’s circumference is known the measure for 1 quarter of the circle’s circumference must be multiplied by 4 and divided by the measure of the circle’s diameter that is already known before the circumference of the circle was known and the resulting ratio is the true value of Pi.

a reply to: JackTheTripper

FURTHER DESCRIPTION OF DERIVING THE CORRECT VALUE OF PI WITH THE KEPLER RIGHT TRIANGLE:

1. The hypotenuse of the right Kepler right triangle is equal to 1 quarter of the circle’s circumference in measure when an isosceles triangle that is made from 2 Kepler right triangles is created inside of a circle, but when the diameter of the circle is the same length of the second longest edge length of the Kepler right triangle then the shortest edge length of the Kepler right triangle becomes equal to 1 quarter of the circle’s circumference. If the second longest edge length of the Kepler right triangle is equal to the measure for the circle’s diameter and also the hypotenuse of the Kepler triangle is divided into Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the larger part of the division will also be equal to 1 quarter of the circle’s circumference because if the hypotenuse of a Kepler right triangle is divided by the measure of the shortest edge length of a Kepler right triangle the result is the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 .

2. Also the hypotenuse of the Kepler right triangle divided by the shortest edge length of the Kepler right triangle produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.

3. The second longest edge length of a Kepler right triangle divided by the shortest edge length of the Kepler produces the ratio the square root of 1.618033988749895 (1.27201964951406).

4. If you multiply the second longest edge length of a Kepler right triangle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
Then you will get the correct length for the diameter of a circle with a circumference four times larger than the measure for the length of the hypotenuse of the Kepler right triangle that is created inside the same circle.

5. So if you already know the measure for the circumference of a circle but you do not yet know the correct length for the circle’s diameter a solution is to divide 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and then multiply the result of dividing 1 quarter of the circle’s circumference by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 by the ratio the square root of 1.618033988749895 (1.27201964951406) resulting in both the second longest edge length of a Kepler right triangle and also the larger measure of the circle’s diameter being divided into by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Remember that if you multiply the second longest edge length of a Kepler right triangle by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 the result is the correct length for the diameter of a circle with a circumference that is 4 times larger than the length of the hypotenuse of the Kepler right triangle that was used to determine the correct length of the circle’s diameter.

“More information on how to derive the correct value of Pi using a Kepler right triangle”:

If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to multiply 1 quarter of the circle’s circumference by the square root of 1.618033988749895 (1.27201964951406) and the result will be the correct length of the circle’s diameter. The length of a circle’s diameter can also be gained from by multiplying 1 quarter of the circle’s circumference by Tangent 51.82729237298776 degrees in Trigonometry. If the circumference of a circle is divided by the diameter of a circle the resulting ratio is Pi. The accuracy of the value of Pi that you get is determined by how accurate the value for the square root of the Golden ratio that you have. The accuracy for the value of the square root of the Golden ratio is determined by the accuracy of the Golden ratio that you have.

If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known another solution is to divide the circle’s diameter by the square root of 1.618033988749895 (1.27201964951406) and the result will be 1 quarter of the circle’s circumference so multiply 1 quarter of the circle’s circumference by 4 and the result is the measure for the circumference of the circle.
The measuring angles for the hypotenuse of a Kepler scalene triangle are 51.82729237298776 degrees and 38.17270762701224 degrees in Trigonometry.
51.82729237298776 degrees is gained when the ratio 1.272019649514069 is applied to the inverse of the Tangent function in Trigonometry. 38.17270762701226 degrees is gained when the ratio 0.786151377757423 is applied to the inverse of the Tangent function in Trigonometry.

A Kepler scalene right triangle can allow a circle with a circumference equal to the perimeter of a square to be created. If a circle and a square are created with equal perimeters of measure than half the perimeter of the square divided by the radius of the circle is Pi and if either the perimeter of the square or the circumference of the circle is divided by the diameter of the circle then the resulting ratio is Pi. Also if a circle and a square are created with equal perimeters of measure and the width of the square is divided by the radius of the circle then the resulting ratio is half of Pi 1.572302755514847. The ratio 1.572302755514847 half of Pi can be gained from 2 divided by the square root of 1.618033988749895 (1.27201964951406).


If the hypotenuse of a Kepler scalene right triangle is divided by the shortest edge length of the Kepler scalene right triangle then the resulting ratio is the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895


1.27201964951406 is the ratio gained from dividing the second longest length of a Kepler scalene right triangle by the shortest edge length of the Kepler scalene triangle. 1.27201964951406 is also the square root of the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895
If 4500 is multiplied by the ratio 1.272019649514069 the result is 5724.0884228133105. (5724).
Repeat: 5724.0884228133105 is the radius of a circle with a circumference of 36000 equal units of measure according to Golden Pi = 3.144605511029693 and Golden Tau = 6.289211022059386.



Kepler triangle: www.goldennumber.net...
en.wikipedia.org...:Kepler_Triangle_Construction.svg
houseoftruth.education...
www.veteranstoday.com...

www.jainmathemagics.com...
en.wikipedia.org...

Alternative geometrical method for determining which Pi is the correct value of Pi 3.141592653589793 Traditional Pi or Golden Pi 3.144605511029693:

Traditional Pi 3.141592653589793 multiplied by 2 is traditional Tau 6.283185307179586.
Golden Pi 3.144605511029693 multiplied by 2 is Golden Tau 6.289211022059386.
Traditional Tau 6.283185307179586 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5729.577951308232523 (reduced to 4 decimal places is 5729).
Alternatively traditional tau 6.283185307179586 says that if a circle has a circumference of 360 then the radius of the circle is 57.295779513082325 (reduced to 4 decimal places is 57.29)
Golden Tau 6.289211022059386 says that if the circumference of a circle has 36000 equal units of measure then the radius of the circle is 5724.088422813310602 (reduced to 4 decimal places is 5724).
Alternatively Golden Tau 6.289211022059386 says that if a circle has a circumference of 360 then the radius of the circle is 57.240884228133106 (reduced to 4 decimal places is 57.24)
It is a Geometrical fact that if one 8th of a circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) then the result is the measure for the radius of the circle. 1.27201964951406 is the ratio gained from dividing the second longest length of a Kepler scalene right triangle by the shortest edge length of the Kepler scalene triangle. If the radius of a circle is divided by one 8th of the circle’s circumference then the resulting ratio is the square root of 1.618033988749895 (1.27201964951406).
We can use the Pythagorean theorem to determine which value of Pi is correct out of Traditional Pi 3.141592653589793 or Golden Pi 3.144605511029693: en.wikipedia.org...
So if the circumference of the circle is 360 and one 8th of 360 is 45. So if the shortest edge length of a Kepler right triangle is 45 then according to the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 the hypotenuse of the Kepler right triangle is 72.811529493745275. If the hypotenuse of a Kepler right triangle is divided by the shortest edge length of a Kepler right triangle then the result is the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895. 72.811529493745275 divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 is 45.
72.811529493745275 squared is 5301.518827218538062.
45 squared is 2025.
5301.518827218538062 subtract 2025 = 3276.518827218538062.
The square root of 3276.518827218538062 is 57.24088422813311. (reduced to 4 decimal places is 57.24).

So if the circumference of the circle is 36000 and one 8th of 36000 is 4500. So if the shortest edge length of a Kepler right triangle is 4500 then according to the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 the hypotenuse of the Kepler right triangle is 7281.1529493745275. If the hypotenuse of a Kepler right triangle is divided by the shortest edge length of a Kepler right triangle then the result is the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895. 7281.1529493745275 divided by the Golden ratio of Cosine (36) multiplied 2 = 1.618033988749895 is 4500.
72.811529493745275 squared is 53015188.272185380623353.
4500 squared is 20250000.
53015188.272185380623353 subtract 20250000 = 32765188.272185380623353.
The square root of 32765188.272185380623353 is 5724.088422813311. (reduced to 4 decimal places is 5724).

a reply to: JackTheTripper

Calculator confirmation for Golden Pi 3.144605511029693 values:
Please remember that if 1 eighth of a circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) the result is the measure for the radius of the circle and if 1 quarter of the circle’s circumference is multiplied by the square root of 1.618033988749895 (1.27201964951406) the result is the measure for the diameter of the circle.
If the measure of the circumference of a circle is already known but the length of the circle’s diameter is not yet known another solution is to multiply 1 quarter of the circle’s circumference by the square root of 1.618033988749895 (1.27201964951406) and the result will be the correct length of the circle’s diameter. The length of a circle’s diameter can also be gained from by multiplying 1 quarter of the circle’s circumference by Tangent 51.82729237298776 degrees in Trigonometry. If the circumference of a circle is divided by the diameter of a circle the resulting ratio is Pi. The accuracy of the value of Pi that you get is determined by how accurate the value for the square root of the Golden ratio that you have. The accuracy for the value of the square root of the Golden ratio is determined by the accuracy of the Golden ratio that you have.

If the measure of the diameter of a circle is already known but the measure of the circle’s circumference is not yet known another solution is to divide the circle’s diameter by the square root of 1.618033988749895 (1.27201964951406) and the result will be 1 quarter of the circle’s circumference so multiply 1 quarter of the circle’s circumference by 4 and the result is the measure for the circumference of the circle.

If 1 quarter of the circle’s circumference is multiplied by the square root of 0.618033988749895 (0.786151377757423) then the result is the larger measure of the circle’s diameter being divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895. Cosine (72) multiplied by 2 = 0.618033988749895 and the square root of 0.618033988749895 is 0.786151377757423.
Here is a description that you can test with a calculator for yourself: The circumference of the circle is 360 and 360 divided by 4 is 90. 90 divided by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 = 55.623058987490531.
55.623058987490531 multiplied by the square root of 1.618033988749895 (1.27201964951406) = 70.75362399816759.
70.75362399816759 multiplied by the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 = 114.4817684562654.

114.4817684562654 is the measure for the diameter of the circle and 360 is the measure for the circle’s circumference.
360 divided by 114.4817684562654 is Golden Pi = 3.144605511029693.
Another example is circumference of circle is 12. 12 divided by 4 = 3.
So we can get the measure for the diameter of a circle with a circumference of 12 by multiplying 1 quarter of 12 that is 3 by the square root of 1.618033988749895 (1.27201964951406) = 3.81605894854218.
Also we get the measure for the diameter of a circle by multiplying 1 quarter of the circle’s circumference by Tangent (51.82729237298776) degrees in Trigonometry. 3 multiplied by Tangent (51.82729237298776) degrees is 3.81605894854218 in Trigonometry.
Now I am going to prove that if the diameter of a circle is 3.81605894854218 and the diameter of the circle is divided into he Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and the division point extended to the circumference of the circle then a isosceles triangle that is made from 2 Kepler right triangles is created and the height of the isosceles triangle is 2.358454133272253. So the second longest edge length of each Kepler right triangle that are both half of the isosceles triangle have a measure also of 2.358454133272253. From the opposing pole of the diameter 2 smaller Kepler right triangles have hypotenuses that touch the circumference of the circle and the measure for both the hypotenuses of these 2 smaller Kepler right triangles is also 2.358454133272253.
Diameter of the circle = 3.81605894854218 subtract 2.358454133272253 = 1.457604815269927. 1.457604815269927 is the measure for the shortest edge lengths for the 2 smaller Kepler right triangles. There are a total of 4 Kepler right triangle inside of the circle.

1.854101966249684 is the measure for half the base width of the isosceles triangle that is made from the 2 larger Kepler right triangles. 1.854101966249684 is also the measure for the shortest lengths of each of the larger Kepler right triangles that make up the isosclese triangle that has a height of 2.358454133272253 and a base width of 3.708203932499369. 2.358454133272253 is half of 3.708203932499369.
Remember the Pythagorean theorem: en.wikipedia.org...
2.358454133272253 squared is 5.562305898748974.
1.854101966249684 squared is 3.437694101250944.
5.562305898748974 plus 3.437694101250944 = 9.
The square root of 9 is 3.
51.82729237298776 degrees is the usual measure angle for the hypotenuse of a Kepler right triangle while the other measuring angle for a Kepler right triangle is 38.17270762701226 degrees. 51.82729237298776 degrees is gained when the ratio 1.272019649514069 is applied to the inverse of the Tangent function in Trigonometry. 38.17270762701226 degrees is gained when the ratio 0.786151377757423 is applied to the inverse of the Tangent function in Trigonometry
Also 1.854101966249684 divided by Cosine (51.82729237298776) is 3.
3 is 1 quarter of 12. Remember again that 1.854101966249684 is half of the base width of the isosceles triangle and also the measure for the shortest edge lengths of the 2 Kepler right triangles that make the isosceles triangle.
Remember to divide the diameter of the circle into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
Circumference of circle is 12. Diameter of circle is 3.81605894854218.
Also if you create a Kepler right triangle that has its shortest edge length as 3 then the hypotenuse will be 4.854101966249685 and if the length of the hypotenuse 4.854101966249685 is divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the larger part of the division of the Kepler right triangle’s hypotenuse into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is also 3.
4.854101966249685 divided by 1.618033988749895 is 3. Also 3 divided by Cosine (51.82729237298776) is 4.854101966249685. So if the shortest edge length of the Kepler triangle is 3 then the measure for the second longest edge length is 3.81605894854218. 3.81605894854218 is the measure for the diameter of a circle with a circumference of 12 remember, so if the shortest length of the Kepler right triangle is equal to 1 quarter of a circle’s circumference then the second longest edge length of the Kepler right triangle is equal to the measure of the circle’s diameter.
12 divided by 3.81605894854218 is Golden Pi = 3.144605511029693.
All you need is a compass and straight edge ruler and obviously a pencil and a pocket calculator.
Create a circle on a piece of paper and divide the diameter into the Golden ratio and then connect the division point with a straight line towards the circumference on either side of the division of the circle’s diameter into the Golden ratio.

a reply to: Deaf Alien

Another example is circumference of circle is 8. 8 divided by 4 = 2.
So we can get the measure for the diameter of a circle with a circumference of 18 by multiplying 1 quarter of 8 that is 2 by the square root of 1.618033988749895 (1.27201964951406) = 2.54403929902812.
Also we get the measure for the diameter of a circle by multiplying 1 quarter of the circle’s circumference by Tangent (51.82729237298776) degrees in Trigonometry. 2 multiplied by Tangent (51.82729237298776) degrees is 2.54403929902812 in Trigonometry.
Now I am going to prove that if the diameter of a circle is 2.54403929902812 and the diameter of the circle is divided into he Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and the division point extended to the circumference of the circle then a isosceles triangle that is made from 2 Kepler right triangles is created and the height of the isosceles triangle is 1.572302755514835. So the second longest edge length of each Kepler right triangle that are both half of the isosceles triangle have a measure also of 1.572302755514835. From the opposing pole of the diameter 2 smaller Kepler right triangles have hypotenuses that touch the circumference of the circle and the measure for both the hypotenuses of these 2 smaller Kepler right triangles is also 1.572302755514835.
Diameter of the circle = 2.54403929902812 subtract 1.572302755514835 = 0.971736543513285. 0.971736543513285 is the measure for the shortest edge lengths for the 2 smaller Kepler right triangles. There are a total of 4 Kepler right triangle inside of the circle.
1.23606797749979 is the measure for half the base width of the isosceles triangle that is made from the 2 larger Kepler right triangles.
1.23606797749979 is also the measure for the shortest lengths of each of the larger Kepler right triangles that make up the isosceles triangle that has a height of 2.54403929902812 and a base width of 2.472135954999579. 1.23606797749979 is half of 2.472135954999579.
Remember the Pythagorean theorem: en.wikipedia.org...
1.572302755514835 squared is 2.472135954999543.
1.23606797749979 squared is 1.527864045000421.
2.472135954999543 plus 1.527864045000421 = 4.
The square root of 4 is 2.
51.82729237298776 degrees is the usual measure angle for the hypotenuse of a Kepler right triangle while the other measuring angle for a Kepler right triangle is 38.17270762701226 degrees. 51.82729237298776 degrees is gained when the ratio 1.272019649514069 is applied to the inverse of the Tangent function in Trigonometry. 38.17270762701226 degrees is gained when the ratio 0.786151377757423 is applied to the inverse of the Tangent function in Trigonometry
Also 1.23606797749979 divided by Cosine (51.82729237298776) is 2.
2 is 1 quarter of 8. Remember again that 1.23606797749979 is half of the base width of the isosceles triangle and also the measure for the shortest edge lengths of the 2 Kepler right triangles that make the isosceles triangle.
Remember to divide the diameter of the circle into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
Circumference of circle is 8. Diameter of circle is 2.54403929902812.
Also if you create a Kepler right triangle that has its shortest edge length as 2 then the hypotenuse will be 3.23606797749979 and if the length of the hypotenuse 3.23606797749979 is divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the larger part of the division of the Kepler right triangle’s hypotenuse into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is also 2.
3.23606797749979 divided by 1.618033988749895 is 2. Also 2 divided by Cosine (51.82729237298776) is 3.23606797749979. So if the shortest edge length of the Kepler triangle is 2 then the measure for the second longest edge length is 2.54403929902812. 2.54403929902812 is the measure for the diameter of a circle with a circumference of 8 remember, so if the shortest length of the Kepler right triangle is equal to 1 quarter of a circle’s circumference then the second longest edge length of the Kepler right triangle is equal to the measure of the circle’s diameter.
8 divided by 2.54403929902812 is Golden Pi = 3.144605511029693.
All you need is a compass and straight edge ruler and obviously a pencil and a pocket calculator.
Create a circle on a piece of paper and divide the diameter into the Golden ratio and then connect the division point to with a straight line towards the circumference on either side of the division of the circle’s diameter into the Golden ratio.
I hope that you already know how divide a given line into the Golden ratio with just compass and ruler and obviously a pencil.

a reply to: Deaf Alien

Another example is circumference of circle is 18. 18 divided by 4 = 4.5.
So we can get the measure for the diameter of a circle with a circumference of 18 by multiplying 1 quarter of 18 that is 4.5 by the square root of 1.618033988749895 (1.27201964951406) = 5.72408842281327.
Also we get the measure for the diameter of a circle by multiplying 1 quarter of the circle’s circumference by Tangent (51.82729237298776) degrees in Trigonometry. 4.5 multiplied by Tangent (51.82729237298776) degrees is 5.72408842281327 in Trigonometry.
Now I am going to prove that if the diameter of a circle is 5.72408842281327 and the diameter of the circle is divided into he Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 and the division point extended to the circumference of the circle then a isosceles triangle that is made from 2 Kepler right triangles is created and the height of the isosceles triangle is 3.53768119990838. So the second longest edge length of each Kepler right triangle that are both half of the isosceles triangle have a measure also of 3.53768119990838. From the opposing pole of the diameter 2 smaller Kepler right triangles have hypotenuses that touch the circumference of the circle and the measure for both the hypotenuses of these 2 smaller Kepler right triangles is also 3.53768119990838.
Diameter of the circle = 5.72408842281327 subtract 3.53768119990838 = 2.18640722290489. 2.18640722290489 is the measure for the shortest edge lengths for the 2 smaller Kepler right triangles. There are a total of 4 Kepler right triangle inside of the circle.
2.781152949374527 is the measure for half the base width of the isosceles triangle that is made from the 2 larger Kepler right triangles.
2.781152949374527 is also the measure for the shortest lengths of each of the larger Kepler right triangles that make up the isosceles triangle that has a height of 3.53768119990838 and a base width of 5.562305898749054. 2.781152949374527 is half of 5.562305898749054.
Remember the Pythagorean theorem: en.wikipedia.org...
3.53768119990838 squared is 12.515188272185195.
2.781152949374527 squared is 7.73481172781463.
12.515188272185195 plus 7.73481172781463 = 20.25.
The square root of 20.25 is 4.5.
51.82729237298776 degrees is the usual measure angle for the hypotenuse of a Kepler right triangle while the other measuring angle for a Kepler right triangle is 38.17270762701226 degrees. 51.82729237298776 degrees is gained when the ratio 1.272019649514069 is applied to the inverse of the Tangent function in Trigonometry. 38.17270762701226 degrees is gained when the ratio 0.786151377757423 is applied to the inverse of the Tangent function in Trigonometry
Also 2.781152949374527 divided by Cosine (51.82729237298776) is 4.5.
4.5 is 1 quarter of 18. Remember again that 2.781152949374527 is half of the base width of the isosceles triangle and also the measure for the shortest edge lengths of the 2 Kepler right triangles that make the isosceles triangle.
Remember to divide the diameter of the circle into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895.
Circumference of circle is 18. Diameter of circle is 5.72408842281327.
Also if you create a Kepler right triangle that has its shortest edge length as 4.5 then the hypotenuse will be 7.281152949374528 and if the length of the hypotenuse 7.281152949374528 is divided into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 then the larger part of the division of the Kepler right triangle’s hypotenuse into the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895 is also 4.5.
7.281152949374528 divided by 1.618033988749895 is 4.5. Also 4.5 divided by Cosine (51.82729237298776) is 7.281152949374528. So if the shortest edge length of the Kepler triangle is 4.5 then the measure for the second longest edge length is 5.72408842281327. 5.72408842281327 is the measure for the diameter of a circle with a circumference of 18 remember, so if the shortest length of the Kepler right triangle is equal to 1 quarter of a circle’s circumference then the second longest edge length of the Kepler right triangle is equal to the measure of the circle’s diameter.
18 divided by 5.72408842281327 is Golden Pi = 3.144605511029693.
All you need is a compass and straight edge ruler and obviously a pencil and a pocket calculator.
Create a circle on a piece of paper and divide the diameter into the Golden ratio and then connect the division point with a straight line towards the circumference on either side of the division of the circle’s diameter into the Golden ratio.
I hope that you already know how divide a given line into the Golden ratio with just compass and ruler and obviously a pencil.

a reply to: davidgrouchy
3.144605511029693 is the correct value of Pi and this fact can be proven by almost anybody that has sufficient knowledge of the principles of the Kepler right triangle including the creation of a circle with a circumference equal in measure to the perimeter of a square.
The correct value of the Golden ratio will determine the correct value of both the square root of the Golden ratio and Pi. Traditional Pi 3.141592653589793 is also false because it is based upon a false value for the Golden ratio for example traditional Pi 3.141592653589793 can also be gained from 4 divided by the square root of 1.621138938277405 = 1.273239544735163. The ratio 1.621138938277405 can be gained in Trigonometry through the formula Cosine (35.84839254086685) multiplied by 2. The ratio 1.621138938277405 is a very poor approximation of the real Golden ratio of 1.618. The correct value for the Golden ratio is Cosine (36) multiplied by 2 = 1.618033988749895 and the correct value for the square root of the Golden ratio is 1.27201964951406. 16 divided by traditional Pi 3.141592653589793 squared = 9.869604401089357 results in the False value of the Golden ratio 1.621138938277405, while 16 divided by Golden Pi 3.144605511029693 squared = 9.888543819998317 = 1.618033988749895. Remember that 1.618033988749895 is the real Golden ratio and NOT 1.621138938277405. We do not even need to use any of the Pi values to determine the diameter of a circle or the circumference of a circle instead we can use the Square root of the Golden ratio = 1.27201964951406. If we multiply 1 quarter of the circle's circumference by 1.27201964951406 then the result is the correct measure for the circle's diameter. If we already know the length of the circle's diameter but we do not yet know the measure for the circle's circumference then all we have to do is divide the measure of the circle's diameter by 1.27201964951406 and the result will be 1 quarter of the circle's circumference. Multiply 1 quarter of the circle's circumference by 4 and obviously we have the value for the circumference of the circle. If we use 1.27201964951406 to get the length of the circle's diameter or the measure for the circle's circumference and then we divide the measure for the circle's circumference by the measure for the circle's diameter I guarantee you the result is 3.144605511029693.

The Kepler right triangle has so much wisdom encoded in it.
The Kepler right triangle is proof that 3.144605511029693 is the correct value for Pi.
3.141592653589793 as Pi has already been proven to be false by the aid of computer software that demonstrate that the curve of a circle can never be filled completely by polygons so the assumption that the gaps in the circle’s curve will disappear is false and thus proves that the multiple Polygon method for deriving a value of Pi is flawed because the multiple polygon method can only give us approximations for Pi while the Kepler triangle gives us the exact value of Pi and that is 3.144605511029693. For example if the second longest edge length of a Kepler right triangle is the same length as the diameter of a circle then shortest edge length of the Kepler right triangle is equal to 1 quarter of the circle’s circumference. So if the shortest edge length of the Kepler right triangle is multiplied by 4 and the result divided by the second longest edge length while we use 1.27201964951406 then we can get the correct value of Pi and again that is 3.144605511029693. The Kepler right triangle is also the key to squaring the circle with equal perimeters. So almost anybody can get the right value of Pi by just constructing a Kepler right triangle and also a pocket calculator. Remember that the hypotenuse of a Kepler right triangle divided by the shortest edge length produces the Golden ratio of Cosine (36) multiplied by 2 = 1.618033988749895, while the second longest edge length of a Kepler right triangle divided by the shortest edge length produces the square root of the Golden ratio 1.27201964951406.
houseoftruth.education...

a reply to: JackTheTripper

. All pi values of Pi are connected to the Golden ratio. The correct value for the Golden ratio will reveal the correct value for the square root of the Golden ratio also known as the Golden root and the correct value for the square root of the Golden ratio will finally reveal the correct value of Pi. Traditional Pi 3.141592653589793 is also false because traditional Pi can be gained from using a false value for the Golden ratio and that false value for the Golden ratio is 1.621138938277405.

4 divided by traditional Pi also gives us a false value for the square root of the Golden ratio and that number is 1.273239544735163. Traditional Pi 3.141592653589793 can also be gained from the formula 4 divided the square root of 1.621138938277405. The square root of 1.621138938277405 is 1.273239544735163, but the correct value for the Golden ratio is Cosine (36) multiplied by 2 = 1.618033988749895 and the correct value for the square root of the Golden ratio is 1.27201964951406. 16 divided by traditional Pi 3.141592653589793 squared = 9.869604401089357 results in the False value of the Golden ratio 1.621138938277405, while 16 divided by Golden Pi 3.144605511029693 squared = 9.888543819998317 = 1.618033988749895. Remember that 1.618033988749895 is the real Golden ratio and NOT 1.621138938277405.
So the correct value for Pi is 3.144605511029693 and NOT 3.141592653589793.

We do not even need Pi to measure the circumference of a circle or the diameter of a circle in relation to each other instead we can gain the measure for the diameter of a circle by multiplying 1 quarter of the circle's circumference by the square root of the Golden ratio = 1.27201964951406. If we already know the length of the circle's diameter but we do not yet know the measure for the circle's circumference then all we have to do is divide the length of the circle's circumference by the square root of the Golden ratio = 1.27201964951406 and the result will be the measure for 1 quarter of the circle's circumference and if 1 quarter of the circle's circumference is multiplied by 4 the result is the measure for the circle's circumference.

a reply to: Liddzer1618

Holy wall of text Batman!

So what value for pi did you get? 3.14159 I hope, for the sake of sanity.

[Edit] I see you got 3.144... Oh dear, 700 years of mathematics and engineering down the drain. I hope you don't actually try and build anything using this value for pi.

refer yourselves to this website for more details on why Pi 3.144606 is the correct one: measuringpisquaringphi.com...