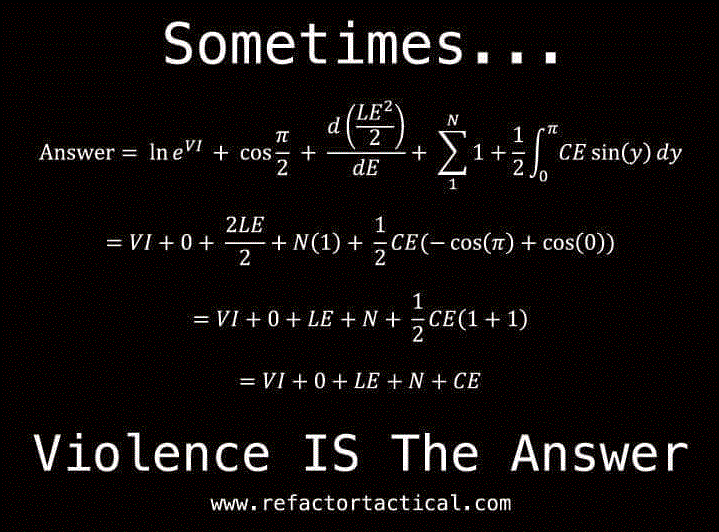It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
5
share:
He figured it out!!!
No sh… kidding!
The world’s most famous math hypothesis has -had, been the Riemann Hypothesis. A hundred and eighty years of countless mathematicians scribbling arcane symbols only other bulb heads could understand had achieved nothing.
Minor progress had been made with solutions to associated problems that spanned the number line with numbers in the 10^100^100 area to start with and growing from there (asymptote analysis) had yielded a proof to the Lindelof Hypothesis several years ago. But Riemann himself thought it was easier to explain but failed at his own attempt (and only one attempt before other problems pushed him into other areas like he knew his time was limited).
And here was the simple answer staring at him from the dry erase board in black and green ink (black for the basic math reiteration and green for the application to the great Riemann Hypothesis-RH).
It was easy to understand as well. Even a precocious child with a grasp of algebraic equations could do the work! That is why the answer had to be correct! Feynman had said that if you could explain your solution to a youngster using basic math then you probably have the answer correct.
It started with simple math we all were taught in grade school: logarithms:
A function is a mathematical structure that manipulates an input and produces (and reproduces) a specific output, in this case Integer X, is transformed by the function, namely:
F(X) = 1/X
For any base 10 integer.
Thats it. The whole key to RH is this function.
Using the Euler Product of the Zeta Function (F(n) = sigma(1/X^n), over x = 1..infinity), it is the sum of logs raised to an integer value, n.
The product, an entire work of genius in its own right, uses two Zeta Functions to create a Sieve of Eratosthenes, which restates the infinite sum as an infinite product of subtracted prime numbers:
P(n) = (1/1 - 1/p^n) )
As one can see, the function is undefined with p=1^1, because you divide by zero. But 1 is not a prime number so this is more of a mathematical complete description of the equation (The product function multiplies the numbers in the range together, so if you had n = 1..5, P(n) = 1x2x3x4x5 = 120); in the Zeta function, p, ranges over the primes, 2,3,5,7,11,13,…
But it is a mess when stated as above. Everyone restates the equation with negative powers to make it look slicker. But you can do this using the log function:
P(n) = log(1-log(p^n) )
Using the power rule of logarithms, log(x^y) = y * log(x), you restate the above product as:
P(n) = log(1 - n * log(p) )
You plainly see that eventually you will take log(n).
Riemann extended the zeta function to the Real Numbers, the Reals, by substituting the integer n, for the real number:
s = a + b*i
Where i is the imaginary number, i = sqrt(-1).
Riemann had hoped that extending the value to an extra dimension (a new variable in the function) would allow the function to be solved in a more simple manner as had been experienced with other equations under real analysis.
But it appeared to cause more problems than it solved.
So keeping it dead simple, substituting s for n, one wonders, “can you take the log of a real number, s”??
Sure! It is clearly explained in any undergrad math textbook. So with, s = a + bi, the equation is:
log(s) = log(a + bi) = 1/2*(a^2 + b^2) + it
Which is just the Pythagorean theorem extending into the real plane! You move forward a units, then up b units, which creates a right triangle. The distance to the point is a straight line, i.e., the hypotenuse, which if you only had a brain, you would know that it is the sum of the squares of a right triangle and is equal to the square of the hypotenuse. And using the real numbers, sines and cosines, equals the above in base 10.
When a^2 + b^2 = 1, you are describing the unit circle. Less than 1, you are inside the unit circle; larger than 1, you are outside the unit circle determined by the value of i*t.
When on the unit circle, s = 1/2 + i*t, which is what Riemann intuitively surmised but stumped mathematicians for hundred plus years!!
And it was staring back at him from the white board.
He took a photo with his phone then parked in front of his computer for a LaTex session to write his results down.
Sunday morning the ArXiv published his paper on Monday morning in the Number Theory section.
The NSA had an eye on Rutgers University and the paper was flagged immediately.
Days later the local newspaper carried a story about a car crash with one fatality.
The arXiv never published the paper.
And the news nobody bothered to understand was the author didn’t even own a car. Had not driven in 23 years.
- The End -
No sh… kidding!
The world’s most famous math hypothesis has -had, been the Riemann Hypothesis. A hundred and eighty years of countless mathematicians scribbling arcane symbols only other bulb heads could understand had achieved nothing.
Minor progress had been made with solutions to associated problems that spanned the number line with numbers in the 10^100^100 area to start with and growing from there (asymptote analysis) had yielded a proof to the Lindelof Hypothesis several years ago. But Riemann himself thought it was easier to explain but failed at his own attempt (and only one attempt before other problems pushed him into other areas like he knew his time was limited).
And here was the simple answer staring at him from the dry erase board in black and green ink (black for the basic math reiteration and green for the application to the great Riemann Hypothesis-RH).
It was easy to understand as well. Even a precocious child with a grasp of algebraic equations could do the work! That is why the answer had to be correct! Feynman had said that if you could explain your solution to a youngster using basic math then you probably have the answer correct.
It started with simple math we all were taught in grade school: logarithms:
A function is a mathematical structure that manipulates an input and produces (and reproduces) a specific output, in this case Integer X, is transformed by the function, namely:
F(X) = 1/X
For any base 10 integer.
Thats it. The whole key to RH is this function.
Using the Euler Product of the Zeta Function (F(n) = sigma(1/X^n), over x = 1..infinity), it is the sum of logs raised to an integer value, n.
The product, an entire work of genius in its own right, uses two Zeta Functions to create a Sieve of Eratosthenes, which restates the infinite sum as an infinite product of subtracted prime numbers:
P(n) = (1/1 - 1/p^n) )
As one can see, the function is undefined with p=1^1, because you divide by zero. But 1 is not a prime number so this is more of a mathematical complete description of the equation (The product function multiplies the numbers in the range together, so if you had n = 1..5, P(n) = 1x2x3x4x5 = 120); in the Zeta function, p, ranges over the primes, 2,3,5,7,11,13,…
But it is a mess when stated as above. Everyone restates the equation with negative powers to make it look slicker. But you can do this using the log function:
P(n) = log(1-log(p^n) )
Using the power rule of logarithms, log(x^y) = y * log(x), you restate the above product as:
P(n) = log(1 - n * log(p) )
You plainly see that eventually you will take log(n).
Riemann extended the zeta function to the Real Numbers, the Reals, by substituting the integer n, for the real number:
s = a + b*i
Where i is the imaginary number, i = sqrt(-1).
Riemann had hoped that extending the value to an extra dimension (a new variable in the function) would allow the function to be solved in a more simple manner as had been experienced with other equations under real analysis.
But it appeared to cause more problems than it solved.
So keeping it dead simple, substituting s for n, one wonders, “can you take the log of a real number, s”??
Sure! It is clearly explained in any undergrad math textbook. So with, s = a + bi, the equation is:
log(s) = log(a + bi) = 1/2*(a^2 + b^2) + it
Which is just the Pythagorean theorem extending into the real plane! You move forward a units, then up b units, which creates a right triangle. The distance to the point is a straight line, i.e., the hypotenuse, which if you only had a brain, you would know that it is the sum of the squares of a right triangle and is equal to the square of the hypotenuse. And using the real numbers, sines and cosines, equals the above in base 10.
When a^2 + b^2 = 1, you are describing the unit circle. Less than 1, you are inside the unit circle; larger than 1, you are outside the unit circle determined by the value of i*t.
When on the unit circle, s = 1/2 + i*t, which is what Riemann intuitively surmised but stumped mathematicians for hundred plus years!!
And it was staring back at him from the white board.
He took a photo with his phone then parked in front of his computer for a LaTex session to write his results down.
Sunday morning the ArXiv published his paper on Monday morning in the Number Theory section.
The NSA had an eye on Rutgers University and the paper was flagged immediately.
Days later the local newspaper carried a story about a car crash with one fatality.
The arXiv never published the paper.
And the news nobody bothered to understand was the author didn’t even own a car. Had not driven in 23 years.
- The End -
a reply to: TEOTWAWKIAIFF
FYI: Status: Writer
As I stated, my logic is correct so I may have the solution to RH here first on ATS!
FYI: Status: Writer
As I stated, my logic is correct so I may have the solution to RH here first on ATS!
Quick summery and round up please?, looks interesting but i've read it twice and i'm still not sure, could be tired but please elaborate?
What is this relating too?
All I've never heard of it before...
What would it resolve?
Thanks TT
What is this relating too?
All I've never heard of it before...
What would it resolve?
Thanks TT
a reply to: TritonTaranis
It is a solution to RH.
At least as far as I know!
It is math/geek stuff and I didn’t know how much I should explain and not sound didactic.
For an overview, quantamagazine.org - How I Learned to Love and Fear The Riemann Hypotheses
Basically, the Zeta Function was extended into Real Analysis by Bernhard Riemann by using the complex number, s = a + bi, instead of the integer value n. This extends the function into the real number plane where the x-axis is just the regular, continuous, number line, with above and below being the “imaginary part” (the sqrt(-1) number). This moves a two dimension line into a two dimensional plane. This degree of freedom, it was hoped, would take the problem from serious number crunching, to some easier math (it does but only if you view as an idiot like I do/did in this story).
Riemann himself did not demonstrate his hunch that “the real part [of the Euler Product of the Zeta Function] is equal to 1/2”. Or, it is no multiplier of 1/2, but only 1/2.
When extending into the real plane, you can “borrow” the unit circle to help explain your function (which was done without explicitly using the unit circle, In Riemann’s case).
Here, this concept is explained, in mathematical terms, for the first time. As far as I know.
I figured this out in 2009. I figured “monkeys washing sand off in the ocean” would happen so wouldn’t be the only yahoo who thinks this way!!
All these years later, I present a “fictional story”!
It is a solution to RH.
At least as far as I know!
It is math/geek stuff and I didn’t know how much I should explain and not sound didactic.
For an overview, quantamagazine.org - How I Learned to Love and Fear The Riemann Hypotheses
Basically, the Zeta Function was extended into Real Analysis by Bernhard Riemann by using the complex number, s = a + bi, instead of the integer value n. This extends the function into the real number plane where the x-axis is just the regular, continuous, number line, with above and below being the “imaginary part” (the sqrt(-1) number). This moves a two dimension line into a two dimensional plane. This degree of freedom, it was hoped, would take the problem from serious number crunching, to some easier math (it does but only if you view as an idiot like I do/did in this story).
Riemann himself did not demonstrate his hunch that “the real part [of the Euler Product of the Zeta Function] is equal to 1/2”. Or, it is no multiplier of 1/2, but only 1/2.
When extending into the real plane, you can “borrow” the unit circle to help explain your function (which was done without explicitly using the unit circle, In Riemann’s case).
Here, this concept is explained, in mathematical terms, for the first time. As far as I know.
I figured this out in 2009. I figured “monkeys washing sand off in the ocean” would happen so wouldn’t be the only yahoo who thinks this way!!
All these years later, I present a “fictional story”!
edit on 1-10-2022 by TEOTWAWKIAIFF because: Typo
edit on 1-10-2022 by TEOTWAWKIAIFF because: Dream within a
dream…
a reply to: infolurker
Which is exactly how RH looks to “normal” people!
I tried to read as much as possible over the past decade or so (arxiv.org, mathematics, number theory) and soon realized that your pic is how I feel!!
Then, while copying out Euler’s product solution, I switched to logarithms. And finally saw the unit circle. And it made sense (to me!)
Sorry that this is not the full thread that explains everything but I figured that there are some people here who would understand what I have scribbled down!!
Remember, violence is not the first solution! Heck, even Gahndi said that you have to get Medieval on some people sometimes!!
Which is exactly how RH looks to “normal” people!
I tried to read as much as possible over the past decade or so (arxiv.org, mathematics, number theory) and soon realized that your pic is how I feel!!
Then, while copying out Euler’s product solution, I switched to logarithms. And finally saw the unit circle. And it made sense (to me!)
Sorry that this is not the full thread that explains everything but I figured that there are some people here who would understand what I have scribbled down!!
Remember, violence is not the first solution! Heck, even Gahndi said that you have to get Medieval on some people sometimes!!
a reply to: TritonTaranis
PS - There is a Million Dollar prize for a solution to the RH.
Hence the title to the story. And the nefarious ending.
PS - There is a Million Dollar prize for a solution to the RH.
Hence the title to the story. And the nefarious ending.
Thanks for your submission.
Good Luck in the Contest!
Johnny
BTW.. when I don't have a clue about whats being discussed or simply haven't been listening due to my confusion, I always rely on this. I'll stand up while grabbing my briefcase and simply say, "I believe if you dive in a bit deeper, you'll see that the only real answer answer is '49' (then briskly leave the office).
Good Luck in the Contest!
Johnny
BTW.. when I don't have a clue about whats being discussed or simply haven't been listening due to my confusion, I always rely on this. I'll stand up while grabbing my briefcase and simply say, "I believe if you dive in a bit deeper, you'll see that the only real answer answer is '49' (then briskly leave the office).
a reply to: JohnnyAnonymous
Uh, I guess that I am a super nerd!
Here is another link that tries to explain what I am going on about here…
IFLScience.com - www.iflscience.com...
It shows the “easy” Zeta function and explains why you can’t just do a Cliffs Notes version of RH.
I have assumed that you can follow a function graph and correlate that with a function. The’log’ really is the key and the base 10 log does reduce down to just “1/2 + it” as Riemann says.
It just the whole “intro to analysis” that I skipped over!
I needed to get this “out there” in case I “have a traffic accident” myself for figuring it out.
🍺
Uh, I guess that I am a super nerd!
Here is another link that tries to explain what I am going on about here…
IFLScience.com - www.iflscience.com...
It shows the “easy” Zeta function and explains why you can’t just do a Cliffs Notes version of RH.
I have assumed that you can follow a function graph and correlate that with a function. The’log’ really is the key and the base 10 log does reduce down to just “1/2 + it” as Riemann says.
It just the whole “intro to analysis” that I skipped over!
I needed to get this “out there” in case I “have a traffic accident” myself for figuring it out.
🍺
new topics
-
Las Vegas UFO Spotting Teen Traumatized by Demon Creature in Backyard
Aliens and UFOs: 1 hours ago -
2024 Pigeon Forge Rod Run - On the Strip (Video made for you)
Automotive Discussion: 2 hours ago -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues: 3 hours ago -
The functionality of boldening and italics is clunky and no post char limit warning?
ATS Freshman's Forum: 4 hours ago -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News: 4 hours ago -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest: 5 hours ago -
Weinstein's conviction overturned
Mainstream News: 6 hours ago -
Supreme Court Oral Arguments 4.25.2024 - Are PRESIDENTS IMMUNE From Later Being Prosecuted.
Above Politics: 7 hours ago -
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest: 8 hours ago -
Chris Christie Wishes Death Upon Trump and Ramaswamy
Politicians & People: 8 hours ago
top topics
-
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest: 8 hours ago, 9 flags -
Weinstein's conviction overturned
Mainstream News: 6 hours ago, 7 flags -
Supreme Court Oral Arguments 4.25.2024 - Are PRESIDENTS IMMUNE From Later Being Prosecuted.
Above Politics: 7 hours ago, 6 flags -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media: 10 hours ago, 6 flags -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest: 5 hours ago, 4 flags -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News: 4 hours ago, 4 flags -
Chris Christie Wishes Death Upon Trump and Ramaswamy
Politicians & People: 8 hours ago, 2 flags -
Any one suspicious of fever promotions events, major investor Goldman Sachs card only.
The Gray Area: 12 hours ago, 2 flags -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues: 3 hours ago, 2 flags -
2024 Pigeon Forge Rod Run - On the Strip (Video made for you)
Automotive Discussion: 2 hours ago, 1 flags
active topics
-
VP's Secret Service agent brawls with other agents at Andrews
Mainstream News • 54 • : mashtun -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News • 8 • : chr0naut -
-@TH3WH17ERABB17- -Q- ---TIME TO SHOW THE WORLD--- -Part- --44--
Dissecting Disinformation • 680 • : 777Vader -
Supreme Court Oral Arguments 4.25.2024 - Are PRESIDENTS IMMUNE From Later Being Prosecuted.
Above Politics • 73 • : xuenchen -
Is there a hole at the North Pole?
ATS Skunk Works • 40 • : Oldcarpy2 -
Fossils in Greece Suggest Human Ancestors Evolved in Europe, Not Africa
Origins and Creationism • 89 • : whereislogic -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media • 197 • : NorthOS -
Candidate TRUMP Now Has Crazy Judge JUAN MERCHAN After Him - The Stormy Daniels Hush-Money Case.
Political Conspiracies • 790 • : Oldcarpy2 -
Weinstein's conviction overturned
Mainstream News • 20 • : Xtrozero -
Cats Used as Live Bait to Train Ferocious Pitbulls in Illegal NYC Dogfighting
Social Issues and Civil Unrest • 22 • : NoviceStoic4
5