A Calculation problem for you to solve

This thread is a problem i designed myself which should provide a few hours of amusement for them who like solving maths or physics problems.

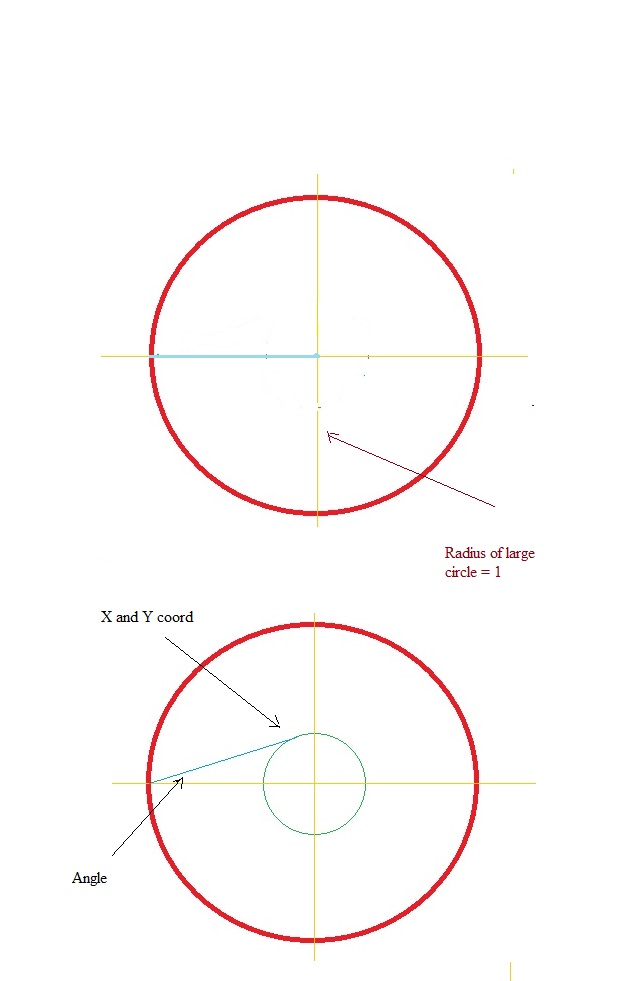
Referring to the pictures below at the origin of the large circle, is a point source where a soap bubble will grow. Imagine your looking top down in plan view at the bubble growing on the flat surface. The bubble will look like a growing circle. The bubble stops growing when its radius equals the radius of the larger circle boundary. The radius of the large circle boundary is equal to 1.

The first picture represents the state just before the bubble starts growing. An imaginary blue line is drawn along the x axis between the point source to the boundary of the larger circle. As the bubble grows the blue line naturally adjusts its point along the circumference of the bubble. The line at the opposite end; where it meets with the larger circle boundary is always fixed (doesn't move) as the bubble grows.


Calculate the X and Y coordinate corresponding to where the blue line connects to the small bubble circumference when the bubble radius is equal to; 0.5, 0.707 and 0.707.

At these x and y coordinates calculate the angle shown in second picture.

This problem may look perplexing at first but like all problems there is a key and once you find it, you'll see the clear path to the solution.

a reply to: AthlonSavage

Right now... at this point and time in my life... I cannot solve the calculation you have presented.

I am interested to read about those who can though.

a reply to: AthlonSavage

I imagine that simply drawing the circle at the given radius and measuring the resulting angle (and intersecting point coordinates) is out of the question??

Otherwise I can give you the answer in less than a day (as soon as I get back from work).

Speaking out of my guts, I would guess that the resulting line will look like this:


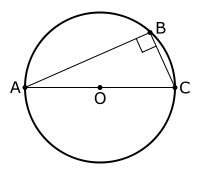
Source: en.wikipedia.org

Thale's theorem

Edit: because there will always be an angle of 90° at the tangent.

a reply to: AthlonSavage

I haven't calculated the X,Y coordinates, but the angles at the given positions (.5, and .707) are approx. 28.96 and 41.4 degrees respectively. The key is to see the blue and yellow lines forming the two legs of an isosceles triangle. They are both 1 unit long. Then, the radius of the bubble becomes the base. If you divide the triangle down the length, you form a right triangle. With the right triangle, you can use:
Sin = Opposite/Hypotenuse
Sin = .25/1 (O = .25 because it is half the radius of the bubble. H=1 the blue line)
sin-1(.25) = 14.48 degrees
Then multiply that by two (since you divided the original isosceles triangle in half.

When the radius of the bubble equals 1 (which may be the third number intended by the poster), the viewer can visualize an equilateral triangle. The blue line, yellow line, and radius of the bubble all measuring 1. This is proven by the formula.
Sin = .5/1
sin-1(.5) = 30 degrees
30 x 2 = 60 degrees

a reply to: iowaporter

This is assuming that the blue line segment always retains its length of 1. Which is not made clear in the original post. If the blue line is always intended to be tangent to the bubble, then it will vary in length, and the solution will be different.

I need some clarification.

Does the line intersect the "bubble" at a tangent point along the small circle (sliding counterclockwise along the upper left quadrant of the "bubble" as it grows), or is it fixed to the "top" of the small circle (sliding along the y-axis as the bubble grow)?

Also, what do you mean by the following:
"...when the bubble radius is equal to; 0.5, 0.707 and 0.707. "?

a reply to: iowaporter

If the blue line varies in length but is always tangent to the bubble circle, then the angle between the blue and yellow lines at bubble radius .5, .707, and 1 are 30, 45, and 90 degrees respectively.

In this case, the blue line (being tangent to the bubble) forms a 90 degree angle at the point of contact with a line drawn from that point to the center of the circle. Thus forming another right triangle.

The angle between the blue and yellow line is theta.
sin theta = O/H
O is the radius of the bubble.
H is the yellow line
sin theta = .5/1
sin -1(.5) = 30.

And so on.

originally posted by: iowaporter

...With the right triangle, you can use:
Sin = Opposite/Hypotenuse ...

Yes. I was going to say that if the length of the blue line is meant to be constant and its intersection point on the smaller circle "slides along" the upper left quadrant of the smaller circle (as I mention in my post above), then it becomes a straightforward and simple trigonometry problem where you need to solve for a right angle, with the blue line being the long leg, the shorter leg being the given radius of the smaller circle and the hypotenuse being the radius of the larger circle (which is fixed at "1").

However (and as you also mention in another post), I don't think the problem is clear enough as to whether the intersection point of the blue line and the smaller circle is meant to be a tangent point (the blue line staying a constant length as the small circle grows, or if it always stays fixed to the y-axis (with the length of the blue line getting greater as the small circle grows).

a reply to: iowaporter

Finally, since the poster probably intends the blue line to vary in length and always be tangent to the bubble.
Then the above angles between the blue and yellow lines are 30, 45, and 90 degrees.
Then the X,Y coordinates would be:
Radius .5, Angle 30, Coordinates (-.25, .43)
Radius .707, Angle 45, Coordinates (-.5, .5)
Radius 1, Angle 90, Coordinates (-1, 0)

Once we form the right triangle between the yellow line (H) and blue line (A) and the radius of the bubble (O) and then calculate the angle between the blue and yellow lines, we can calculate the third angle of the right triangle. In the first case, 180 - 90 - 30 = 60. Then we subtract that from 180 to get the angle from the positive X axis. Then, for a unit circle, we know that Cos(theta) = X and Sin(theta) = Y.

BUT - since the bubble isn't a unit circle until the radius is 1, we have the multiply the resulting coordinates by the actual radius.
So, when the angle between the blue and yellow lines is 45, the opposite angle is also 45 (135 when measuring from the positive x axis) and the X and Y coordinates would be (-.707, .707) for a unit circle. But, since the radius is .707, we have to multiply that times the results to get the final coordinates of (.5, .5).

(0.5) X=-0.2500 Y=0.4330 60°0'0"
(0.707) X=-0.4998 Y=0.5000 45°0'31"

0.5, 0.707 and 0.707 ?

a reply to: manuelram16

I assume the last measure was intended to be 1. (.5, .707, and 1)

originally posted by: iowaporter
a reply to: iowaporter

Finally, since the poster probably intends the blue line to vary in length and always be tangent to the bubble.
Then the above angles between the blue and yellow lines are 30, 45, and 90 degrees.
Then the X,Y coordinates would be:
Radius .5, Angle 30, Coordinates (-.25, .43)
Radius .707, Angle 45, Coordinates (-.5, .5)
Radius 1, Angle 90, Coordinates (-1, 0)

Once we form the right triangle between the yellow line (H) and blue line (A) and the radius of the bubble (O) and then calculate the angle between the blue and yellow lines, we can calculate the third angle of the right triangle. In the first case, 180 - 90 - 30 = 60. Then we subtract that from 180 to get the angle from the positive X axis. Then, for a unit circle, we know that Cos(theta) = X and Sin(theta) = Y.

BUT - since the bubble isn't a unit circle until the radius is 1, we have the multiply the resulting coordinates by the actual radius.
So, when the angle between the blue and yellow lines is 45, the opposite angle is also 45 (135 when measuring from the positive x axis) and the X and Y coordinates would be (-.707, .707) for a unit circle. But, since the radius is .707, we have to multiply that times the results to get the final coordinates of (.5, .5).

Also, when the blue circle's radius is 1, then it is the same as the red circle. Therefore, the blue line would no longer be a valid line (the length would be zero) and there would be no angle to measure.

If this were a calculus problem, then the angle that the OP wants us to measure would approach 90° (but never get there) as the blue circle's radius grows to approach "1", and the length of the blue line shortens as it approaches zero.

So the angle would grow from 30° at radius 0.5, then 45° at radius 0.707, then beyond that radius,m to will continue to grow towards the limit of 90° -- e.g., to 60°, then 80°, then 89°, then 89.9°, then 89.99°, then 89.9999999° and so on, but it never gets to 90° and all collapses into "no angle" when the radius of the blue circle matches the radius of the red circle.

a reply to: Soylent Green Is People

But if we define the blue line as a line with a fixed point on the outer circle and tangent to the bubble, then a real line does exist at that point and tangent to the bubble. The angle between the blue and yellow lines is 90. And the X and Y coordinates of that point are -1 and 0.

originally posted by: iowaporter
a reply to: Soylent Green Is People

But if we define the blue line as a line with a fixed point on the outer circle and tangent to the bubble, then a real line does exist at that point and tangent to the bubble. The angle between the blue and yellow lines is 90. And the X and Y coordinates of that point are -1 and 0.

ONLY as the length of the blue line approaches zero, but not when it reaches zero.

The blue line has a length and forms a measurable angle when the length of the blue line is greater than zero (i.e., when the radius of the blue circle is less than 1), but when the blue circle's radius is "at" 1, then there is no longer a measurable blue line, and thus it cannot form a measurable angle.

a reply to: Soylent Green Is People

By definition, a line is always infinite. On that line, there is a line SEGMENT with endpoints on the large circle and the bubble. The picture illustrates the segment, but the description describes the line.

originally posted by: iowaporter
a reply to: Soylent Green Is People

By definition, a line is always infinite. On that line, there is a line SEGMENT with endpoints on the large circle and the bubble. The picture illustrates the segment, but the description describes the line.

I get what you're saying because as the problem is written, the blue line already "exists" but is just getting smaller as the blue circle radius approaches that of the red circle.

However, if the problem started out as simply showing a circle with radius "1", and asked what the length of a line be if it started at (-1,0) and went in a direction 90° from the X-axis in the positive-"y" direction until it hit a tangent point on the circle, you would say that no such line exists, because there are no tangent points on the circle in that direction.


So it is a matter for calculus:

As the radius of the blue circle approaches that of the red circle (i.e., as it approaches 1), the length of the blue line approaches zero and the angle that the OP is asking for would be approaching 90°.

But because it is calculus, it never reaches those limits, so the radius can be 0.99999999999999999...(forever), and the blue line is 0.0000000000....0001, the angle is 89.9999999999999...(forever)° -- but we can never get to the limits of the calculus problem, which is a radius of circle being "1" and the angle being 90°, because the length of the line would be zero, which makes it undefinable as a line.