The Buzz Aldrin's object. Part III. Apparent magnitude and second set of odds.

I was challenged to present the odds of the object observed during the Apollo 11 mission to be a SLA panel, travelling in the same direction that the CSM-LM on their way to the moon, and showing a close to constant apparent magnitude (not flashing).

If you didn't read part I and II, you can find it here.

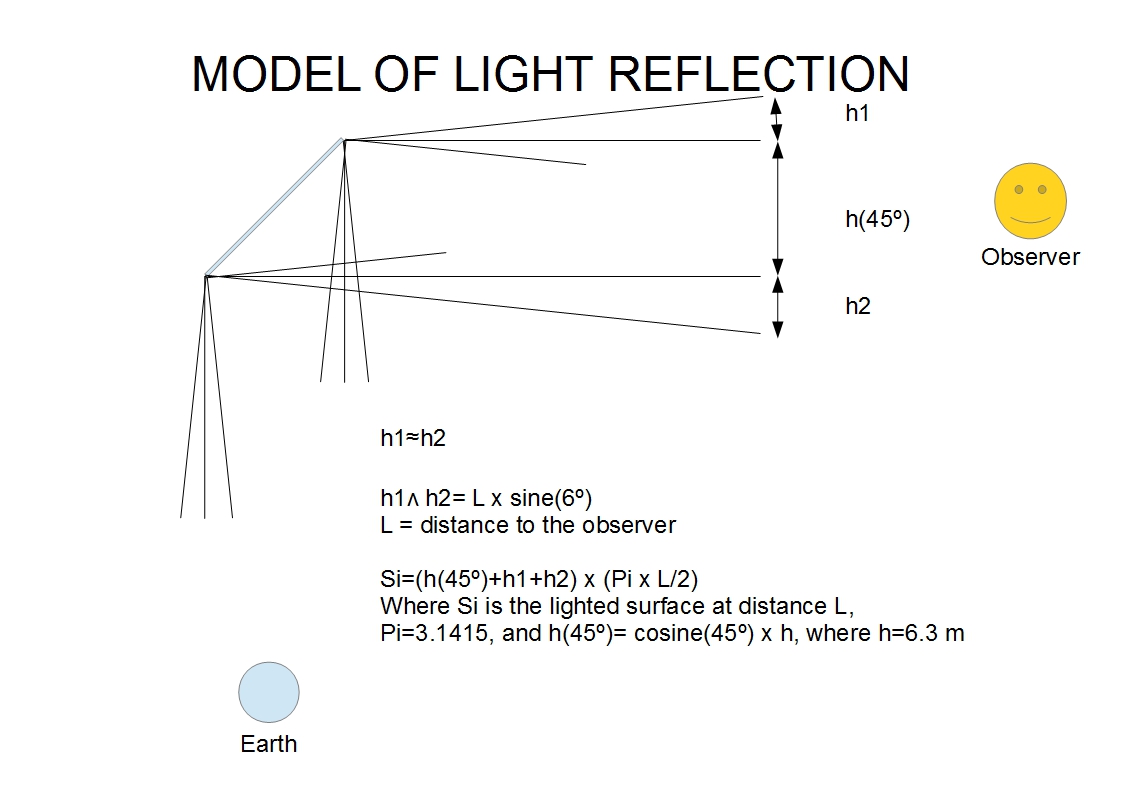
The model below, is a simple but representative model for light reflection on the panel, where the source of the light is the sunlight reflected on Earth.



Calculus of luminous power, apparent magnitude and a second set of odds.

Postulates

1. Let's agree that the convex reflective surface has an albedo of 0.8 and the concave surface of 0.1.
2. Let's agree that there is no diffuse light in space. This means that the sun light is reflected by the object and strikes directly the eye of the observer, or the object will not be seen.
3. Let's agree that visible light (visible spectrum) corresponds to 40% of the total irradiance of the sun.
4. Lets agree that the position of the object in relation to the observer is a random event (the reflecting surfaces could be facing any direction).
5. Let's agree that the period of observation begun 7 hours after launch and continued until it was time to sleep (13:30 hours after launch).
6. Let's agree that at the beginning of the observation, the Earth occupied a field of view of 12º (which corresponds to a distance of 60838 km from the Earth).


Calculus

The luminous power of the Sun reflected by the Earth (visible spectrum), is given by the equation:
Pr = (Pi x R^2) x P x Al, where Pr is the luminous power reflected, Pi=3.1415, R is the radius of the Earth, P is the solar constant and, for the visible spectrum is equal to 1.361 kw/m2 x 0.4 = 0.544 kw/m2, and Al=0.3 is the albedo of the Earth.

Pr= 20,825,932,388,004 kW

The luminous power flux (Pf), luminous power by surface unit, at the distance D= 60,838 km between the Earth and the observer/panel/object is given by the equation: Pf=Pr / (2 x Pi x D^2), where Pi=3.1415.

Pf= 896 kW/km^2 Pf= 0.896 W/m^2

The luminous power reflected by the panel (Pp), in a 45º degree angle, is a function of the apparent surface area of the panel (Sa)= (h x cosine(45º)) x w, where h and w are parameters of the panel, the luminous power received from Earth (Pf) and the albedo (Al) of the panel surface: Pp= Sa x Pf x Al.

Pp= 20.92 m^2 x 0.896 W.m^-2 x Al; for Al= 0.8, Pp= 15 W; for Al= 0.1, Pp= 1.87 W.

The luminous power flux of the panel (Ppf), at a distance L from the observer, is a function of the lighted surface area at a distance L of the panel (Sp)= (h x cosine(45º) + (2 x (L x sine(6º))) x (Pi x L/2), where Pi=3.1415, and the luminous power of the panel (Pp): Ppf= Pp/Sp.

For L= 22,000 m, Sp= 159,092,106 m^2, and for Al=0.8, Ppf= 9.4 x 10^-8 W/m^2. For Al=0.1, Pf= 1.2 x 10^-8 W/m^2.

For L= 10,000 m, Sp= 32,908,340 m^2, and for Al=0.8, Ppf= 4.5 x 10^-7 W/m^2. For Al=0.1, Pf= 5.7 x 10^-8 W/m^2.

For L= 500 m, Sp= 85,591 m^2, and for Al=0.8, Ppf= 1.8 x 10^-4 W/m^2. For Al=0.1, Pf= 2.2 x 10^-5 W/m^2.

For comparison, the full Moon show a luminous power flux on the Earth surface of 6.84 x 10^-4 W/m^-2. This tell us that for the different scenarios, the apparent magnitude of the panel would vary between ca. -12 to 0. This is in better accordance with the descriptions made by Buzz Aldrin.


Second set of odds

“The probability associated to the observer being in the path of light, reflected by the Earth, and again reflected by the panel.”

The surface of half a sphere at a distance L (Sl) is given by the equation: Sl= 2 x Pi x L^2, where Pi=3.1415.

For L= 500 m, Sl= 1,570,796 m^2.
For L= 10,000 m, Sl= 628,318,531 m^2.
For L= 22,000 m, Sl= 3,041,061,689 m^2.

The probability of the observer to be in the path of the reflected light at distances L= 22,000 m, L=10,000 m and L=500 m is given by the equation:
P=Sp/Sl, where P is the probability, Sp is the lighted surface area at a distance L of the panel, calculated before, and Sl the surface of half a sphere.

Thus,
P(22,000 m)=0.0523
P(10,000 m)=0.0524
P(500 m)=0.0545


The analysis show that the probability that the "non flashing object" was not the panel, is an interval of P=94,55% and P=94,77%. In other words, it would be the panel 1 time in every 20 attempts.
The same analysis can be made regarding the light reflected from the Moon as the source of light reflected by the panel/object (and will be made to cover all bases).

Although these odds, though they are very small, associated with the features of the light reflected may explain the object as the panel, they don't explain the almost impossible motion of the panel. The odds for the motion of the panel will be calculated soon.