The Solar System at Giza: The World's Oldest Book of Astronomy

originally posted by: Blackmarketeer
a reply to: Ahatmose

I really want all to notice the level of expertise of my detractors

You couldn't even recognize the Egyptian sun god Ra.

Suggesting that the ancient Egyptians used a modern metric meter or had knowledge of it makes your theory imbecilic. They couldn't even standardize the cubit.

And the Foot is based on an old roman measure. Read how the English determined the foot: "You take 16 men as they enter church. You have each one put one foot down on the ground in a line. You then take 1/16th of that line to be your 'foot. " That's not made up, that was how they got a "foot" in lieu of any standardized measurement.

So when you produce an equation that adds one meter to one cubit to get feet - well, that is just bad practice.

Among the very many things that the three Giza Pyramids show us is this relationship.

Mercury and Mars ratio: (click on image for larger version)

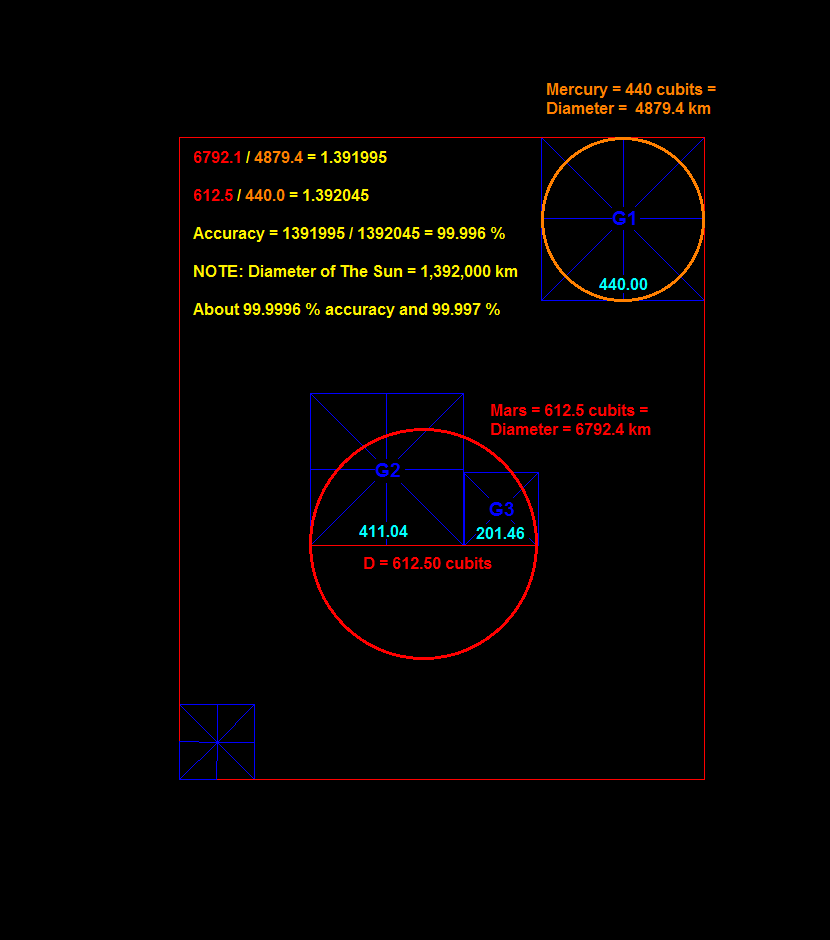
and this one between the foot and the cubit ...

too bad there are those who are too stubborn or too stupid to see it.

1052.5 / 612.50 = 1.718367

1.718367 x 12 = 20.62 inches

.

.

Now, at the level of these measurements, 5407.9 at N.E., or 5409.2 at S.W., above the base, the edges of the casing (by the angles of the N. and S. side found above) will be 285.3 ± 2.7 on the North, and 30I.6 on the South side, from the vertical axis of the centre. Thus there would remain for the casing thickness 60.8 ± 3 on the N., and 86.6 on the S.; with 77.6 for the mean of E. and W. Or, if the angle on the S. side were the same as on the N., the casing thickness would be 69.2 on the S. This, therefore, seems to make it more likely that the South side had about the same angle as the North. On the whole, we probably cannot do better than take 51º 52' ± 2' as the nearest approximation to the mean angle of the Pyramid, allowing some weight to the South side. The mean base being 9068.8 ± .5 inches, this yields a height of 5776.0 ± 7.0 inches.

www.ronaldbirdsall.com...

Phi angle = 51.8273 = 51º 49' 38.28"

Pi angle = 51.8540 = 51º 51' 14.4"

5.5/7 = 51.8428 = 51º 50' 34.08"

Petrie gives it from 51º 50' to 51º 54' = WITH THE PI ANGLE BEING THE CLOSEST TO HIS MEAN.

51.8333º to 51.9000º

LOL and you sit there and claim to know precisely what it is based on what ? Mathematical papyri that are over 700 years removed from the building of the pyramids. And I am always amazed that people like you are so convinced that that was the pinnacle of Egyptian mathematics. Perhaps you can point us to a mathematical papyrus from either The 3rd of IVth Dynasty. On what are you basing the fact that what was discovered from the 12th or 12th dynasty is the height of the knowledge reached in The Pyramid Age of the 3rd and 4th dynasties ?

Anyway I have been through this a zillion times with people just like you, in fact have we met ?

Anyway you continue to believe and spout your insinuated facts when in realty nothing is really known for sure from the early period. Or do you have the plans to the pyramids ? I assume you agree there had to be a plan.

anyway I really don't think we will converse again. You can continue to spout the nonsense found at guardian ... I have heard it all before.

.

The papyrus date from around 1850 BCE and are copies of texts thought to be from around 2000 BCE. Khufu reigned 2589–2566 BCE.

If they understood Pi during Khufu's reign then it would stand to reason it would still be used (and written in their math texts) later. They would not still be teaching the "method of squares" for approximating the area of a circle if they had already understood Pi.

A text from 2000-1850 BCE is far more contemporary as to what Egyptian mathematics were than anything you are conjecturing over.

You've blinded yourself to the actual design of the GP in favor of your fantasy.



As we see, the GP is one pyramid out of many that have a seked of 5-1/2. Snefru, Khufu, Djedefre, Niuserre, Djedkare all have the same seked of 7:5-1/2. There are several scholarly texts on academia that discuss the sacredness of such numbers, 7, 11, 14... etc. Whether or not this was intentional or not we'll never know.

They would not still be teaching the "method of squares" for approximating the area of a circle if they had already understood Pi.

So the Earth was flat till Copernicus published the heliocentric theory in 1540 AD or was that just the year the church allowed the knowledge be understood by the common man?

OP your technique reminds me of some cryptographic "conclusions" made about the Kryptos puzzle in the CIA courtyard.
You can find clues in segments shorter than the unicity distance needed to solve the puzzle and build on them in a way that was never intended.

I remember seeing a "dig here" sign in the puzzle that looked intentional.

Is there such a thing as shared schizophrenia?

originally posted by: Cauliflower

They would not still be teaching the "method of squares" for approximating the area of a circle if they had already understood Pi.

So the Earth was flat till Copernicus published the heliocentric theory in 1540 AD or was that just the year the church allowed the knowledge be understood by the common man?

Non-sequitur.

People have known the Earth is round since the Ancient Greeks established that fact. Nothing Copernicus ever did had anything to do with showing the Earth is round, since he (and everyone else with any education) knew that already.


Harte

Nothing Copernicus ever did had anything to do with showing the Earth is round, since he (and everyone else with any education) knew that already.

a reply to: Harte

Anybody that looked up and saw the shadow of the earth in the crescent moon.
Greeks such as Eratosthenes refined that observation.
There were competing flat Earth theories being taught by trolls.

originally posted by: Blackmarketeer
The papyrus date from around 1850 BCE and are copies of texts thought to be from around 2000 BCE. Khufu reigned 2589–2566 BCE.

If they understood Pi during Khufu's reign then it would stand to reason it would still be used (and written in their math texts) later. They would not still be teaching the "method of squares" for approximating the area of a circle if they had already understood Pi.

A text from 2000-1850 BCE is far more contemporary as to what Egyptian mathematics were than anything you are conjecturing over.

You've blinded yourself to the actual design of the GP in favor of your fantasy.

As we see, the GP is one pyramid out of many that have a seked of 5-1/2. Snefru, Khufu, Djedefre, Niuserre, Djedkare all have the same seked of 7:5-1/2. There are several scholarly texts on academia that discuss the sacredness of such numbers, 7, 11, 14... etc. Whether or not this was intentional or not we'll never know.

Someone states thus:

The papyrus date from around 1850 BCE and are copies of texts thought to be from around 2000 BCE. Khufu reigned 2589–2566 BCE.

Could you enlighten us to the evidence that they are copies from 2000 BC ?

If they understood Pi during Khufu's reign then it would stand to reason it would still be used (and written in their math texts) later. They would not still be teaching the "method of squares" for approximating the area of a circle if they had already understood Pi.

Again perhaps you could enlighten us to the evidence that the knowledge of the Egyptians was linear. That is to say that the knowledge from the 13th Dynasty was the same or greater that of The 3rd and IVth Dynasty.

Also how do you know that the papyri we have was the pinnacle e of the knowledge at the time ?

You've blinded yourself to the actual design of the GP in favor of your fantasy.

Interesting that you will accept 7, and 11 and 8 1/2 and 14 and 5 1/2 but refuse to accept or acknowledge 9 by 11

As we see, the GP is one pyramid out of many that have a seked of 5-1/2. Snefru, Khufu, Djedefre, Niuserre, Djedkare all have the same seked of 7:5-1/2. There are several scholarly texts on academia that discuss the sacredness of such numbers, 7, 11, 14... etc. Whether or not this was intentional or not we'll never know.

Just curious have you actually ever calculated the angles using the sides that are given for these other pyramids ? Try it you might be a bit surprised that the published material is in error.

And finally many of them are listed by you as seked 5 1/4. I find it much easier to simply call them examples of a 3, 4 and 5 sided right angled triangle with angles of 53.13 and 36.87 degrees.

However perhaps you can clear up a mystery for us. How did they go from this:



to this diagram ?



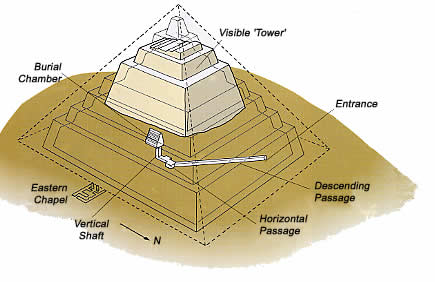
And be able to ascertain an angle of 51°50'35

When this is the data given:

Height 65 metres (213 ft) (ruined)
(From base to summit: 93.5 metres (307 ft))

Base 144 metres (472 ft)

Slope 51°50'35

since tan of an angle is 1/2 base divided by height we get:

72 / 93.5 = 0.77005347594

and this yield an angle of 52.402

So say again who has not done their homework.

.

Pre-Socratic thinkers were almost in universal agreement circa 600-400BC that the world was a sphere. (Thales)
Democrateus also theorized that all matter was made up of tiny 'Atoms'. 460bc

Point is the ancients weren't stupid. And they weren't without 'Ideas" - It was the technology they lacked to prove them which held them back. And thus the march towards progress in the Age of Reason took precedence.

I've never come across anything in AE suggesting they got any closer to Pi than 3.2 (And I love Carl Munck!!!)

H. W. E. Saggs, in Civilization before Greece and Rome (1989), dismisses the astronomical acumen of the Egyptians, writing:

"In view of the low level of their mathematics, it is not surprising to find that the Egyptians made very little contribution to theoretical mathematical astronomy; as far as current evidence goes, they produced no texts which deserve this description until the final centuries before the Christian era, after they had become open to Babylonian and Hellenistic influences."






But because the OP is taking so much heat I'll throw something out there to help lend support to his argument:


Colin Reader has suggested that the construction of the three Giza pyramids show a design which encompasses all three pyramids from the very start.

"Under the conventional chronological scheme 'Khafre's causeway' [leading to the second pyramid] did not exist at the time of Khufu's [Cheops] quarrying [for the first pyramid]. If this had been the case, why was the extent of the quarrying limited by a feature (the causeway) which was only conceived in Khafre's reign?"
"The conventional sequence of development requires us to accept that Khufu's workmen went to the trouble of opening up a second quarry, leaving an intact limestone ridge -- which we now know as Khafre's causeway -- between the two quarries. Why did they not simply extend the northern quarry southwards by removing the linear body of limestone which, at the time, served no apparent purpose?"

"The positioning of the two quarries clearly suggests that, like the excavation of the Sphinx and the construction of the Sphinx Temple, the alignment of 'Khafre's causeway' was established some time before Khufu's work at Giza. Under this revised sequence of development, interpretation of the spatial relationship between the causeway and Khufu's quarries becomes quite straightforward, with the existing causeway limiting the extent of the later quarrying work."

-- Colin Reader, "Giza Before the Fourth Dynasty" JACF (2002)



Their are many more arguments to be made regarding the initial grand design but the Causeway always stood out for me. In the 80 years of construction = three Pharaohs are not competing for national resources and building progressively smaller pyramids as the original impetus fades. So if there is some master plan from the beginning - spacial relationships to each other would be important.

originally posted by: Ahatmose



And be able to ascertain an angle of 51°50'35



When this is the data given:



Height 65 metres (213 ft) (ruined)

(From base to summit: 93.5 metres (307 ft))



Base 144 metres (472 ft)



Slope 51°50'35



since tan of an angle is 1/2 base divided by height we get:



72 / 93.5 = 0.77005347594



and this yield an angle of 52.402



So say again who has not done their homework.

Apparently, you haven't, since it appears that you don't actually know how the Egyptians measured angles.

By the way, you have your calculated tangent upside down. It should be opposite/adjacent, where, for your angle, the opposite site is the height, not half the base.

Harte

By the way, you have your calculated tangent upside down. It should be opposite/adjacent, where, for your angle, the opposite site is the height, not half the base.

LOl What great input into the discussion. I left out a step too bad I thought everyone would see it but for the slower members of the audience allow me to put it simply for them

93.5 / 72 (1/2 base) = 1.2986111111

Tan of 1.2986111111 = 52.40 now would you care to explain why all published reports place the angle at 51°50'35 and as a matter of fact almost all numbers quoted in Lehner's "book" have wrong angles from the given data yet no one bothers to check and those that do never bring it up. Actually all of Egyptology is like that.



.

a reply to: Ahatmose

Could you enlighten us to the evidence that they are copies from 2000 BC ?

EGYPTIAN MATHEMATICS PAPYRI (and contents exhibited) (buffalo.edu)

The Rhind Papyrus (also called the Ahmes Papyrus) is named after the British collector, Rhind, who acquired it in 1858. It was copied by a scribe, Ahmes (or Ahmos), (~1650 BC) from another document written ~2000 BC, which, possibly in turn, was copied from a document from ~2650 BC (the time of Imhotep?). The Rhind Papyrus is located in the British Museum, and contains mathematics problems and solutions. All the problems below are translations.

Here we see the dating goes back even further, possibly to the very time of Khufu himself. How is that for relevant, slick? The scribe himself (Ahmes) declares it is a copy of a text from 2 centuries earlier. (source)



And: Papyruses, Mathematical (dictionary.com)

Papyruses, Mathematical

extant mathematical works of ancient Egypt, dating from the period of the Middle Kingdom (c. 21st century to c. 18th century B.C.). The most famous are the Rhind Papyrus, now in the British Museum (London), and the Moscow Papyrus, now in the A. S. Pushkin Museum of Fine Arts (Moscow).

The Rhind Papyrus, named after its owner, the Egyptologist H. Rhind, was first studied and published in German by A. Eisenlohr; it is also called the Ahmes Papyrus, after its compiler, the scribe Ahmes (c. 2000 B.C.)

None of the mathematical papyrus from Egypt ever - EVER - demonstrated a working formula for calculating Pi as a ratio between circumference and diameter. They only got as far as approximating a circle's area by the "method of squares" shown earlier.

The Ahmes papyrus states it is a: "thorough study of all things, insight into all that exists, knowledge of all obscure secrets." - Odd, don't you think, it would completely omit something as groundbreaking as the concept of Pi (or Phi, or Trigonometry, and so on...)

Another method devised is to approximate a circle by overlaying a 3x3 grid on it and constructing an octagon and determining the area of the octagon in place of the circle. Crude, but workable.



Now ask yourself, if Pi was so fundamental to making the Great Pyramid, and the GP was a part of the Giza "solar model" as you claim, then why are Khafre's and Menkaure's pyramids not also make using Pi? Why do their slopes diifer? Khafre used a seked of 7:5 versus Khufu's 7:5-1/2 and Menkaure used 7:5-3/5.

'The apparent placement of these other sites in relationship to the meridian of the Great Pyramid becomes even more understandable when we recognize that the Great Pyramid was located at 30* north latitude (currently 29° 58' 51"). At first glance it appears that the builders made an error of 1' 9" in its location. However, without a correction for atmospheric refraction, 29° 58' 22" north latitude appears to be exactly 30*, based on purely astronomical observation. Thus there could instead be an error of 29" in the other direction. Or, there could be an error of only 20" if, as Piazzi Smyth suggests, they had intended to split the difference and try for the intermediate value of 29° 59' 11". This idea becomes more plausible when one realizes that the atmospheric error is in the opposite direction for an alignment based on solar observations, and thus it would make sense that they might have used an intermediate value between the solar and stellar calculations. It is equally likely that they simply could not place the Great Pyramid any farther north, and still remain on their prime meridian bisecting Egypt, because the Giza Plateau ends. As it stands, the Great Pyramid is closer to the cliff at the northern edge of the Giza Plateau than many engineers would have thought feasible. It is even remotely possible that the earth's crust has shifted slightly over the intervening 4500 years and the Pyramid was originally placed at a minutely different latitude. In any case, the precision with which it is placed is astounding, certainly more than accurate enough to prove both their intention and their ability'. (5)

So did the ancient Egyptians know what a degree of latitude was?
If so then they knew there were 47 degrees latitude between the tropics.

Kind of difficult to make it fit after the fact.

They obviously never published the Greek pi symbol.
Maybe it was an Egyptian secret (big science of the day).

originally posted by: Blackmarketeer
a reply to: Ahatmose

Could you enlighten us to the evidence that they are copies from 2000 BC ?

EGYPTIAN MATHEMATICS PAPYRI (and contents exhibited) (buffalo.edu)

The Rhind Papyrus (also called the Ahmes Papyrus) is named after the British collector, Rhind, who acquired it in 1858. It was copied by a scribe, Ahmes (or Ahmos), (~1650 BC) from another document written ~2000 BC, which, possibly in turn, was copied from a document from ~2650 BC (the time of Imhotep?). The Rhind Papyrus is located in the British Museum, and contains mathematics problems and solutions. All the problems below are translations.

Here we see the dating goes back even further, possibly to the very time of Khufu himself. How is that for relevant, slick? The scribe himself (Ahmes) declares it is a copy of a text from 2 centuries earlier. (source)

And: Papyruses, Mathematical (dictionary.com)

Papyruses, Mathematical

extant mathematical works of ancient Egypt, dating from the period of the Middle Kingdom (c. 21st century to c. 18th century B.C.). The most famous are the Rhind Papyrus, now in the British Museum (London), and the Moscow Papyrus, now in the A. S. Pushkin Museum of Fine Arts (Moscow).

The Rhind Papyrus, named after its owner, the Egyptologist H. Rhind, was first studied and published in German by A. Eisenlohr; it is also called the Ahmes Papyrus, after its compiler, the scribe Ahmes (c. 2000 B.C.)

 

None of the mathematical papyrus from Egypt ever - EVER - demonstrated a working formula for calculating Pi as a ratio between circumference and diameter. They only got as far as approximating a circle's area by the "method of squares" shown earlier.

The Ahmes papyrus states it is a: "thorough study of all things, insight into all that exists, knowledge of all obscure secrets." - Odd, don't you think, it would completely omit something as groundbreaking as the concept of Pi (or Phi, or Trigonometry, and so on...)

Another method devised is to approximate a circle by overlaying a 3x3 grid on it and constructing an octagon and determining the area of the octagon in place of the circle. Crude, but workable.

Now ask yourself, if Pi was so fundamental to making the Great Pyramid, and the GP was a part of the Giza "solar model" as you claim, then why are Khafre's and Menkaure's pyramids not also make using Pi? Why do their slopes diifer? Khafre used a seked of 7:5 versus Khufu's 7:5-1/2 and Menkaure used 7:5-3/5.

Thank you for the link to the papyri. I find looking at the math systems of tthe culture that built something far more interesting than coincidental calculations based off of modern measurement systems. You will find pi in anything containing a square base . That does not mean the person who makes the square base or the circle that fits in it knows about pi. Accurate angles arcs and circles can be done with a couple one cubit long straight rods, a couple long strings, and a plumb bob( or I tie the end of the string around a small rock). Some colored thread I cool sew into knots at one cubit intervals on one of the strings would bothbe appreciated but not necessary. With just those simple tools very complex designs can be laid out and constructed without the laborers understanding the complex mathematic principle behind it. Just addition and subtraction with a smasmattering of fractions for dividing the cubit which could be supplied by the engineer as a cubit long straigstring or rod with the proper intervals already marked.

a reply to: Jarocal

That does not mean the person who makes the square base or the circle that fits in it knows about pi.

The obvious smoking gun for the knowledge of pi is the location of the great pyramid on the 30 degree line of latitude.
The Egyptians must have made the choice so that there would be 47 degrees of latitude between the tropics.
I do think the choice of the meter length to make the speed of light close to 300 million meters per second could be a kludge.

If the Great Pyramid was deliberately placed 2125 meters south of the 30th parallel by the Egyptians, then maybe the reason Odysseus spent 17 days on a raft in Homers Odyssey was that 17 is an important Fermat prime?

Oh wait that can't be, know one had the math skills more than 50 years BC.

originally posted by: Ahatmose

By the way, you have your calculated tangent upside down. It should be opposite/adjacent, where, for your angle, the opposite site is the height, not half the base.

LOl What great input into the discussion. I left out a step too bad I thought everyone would see it but for the slower members of the audience allow me to put it simply for them

Yeah, it's up to us "slower members" to correct the errors in your utterly basic mathematics.
So, allow me:

originally posted by: Ahatmose



93.5 / 72 (1/2 base) = 1.2986111111



Tan of 1.2986111111 = 52.40

No, you appear here to have a lack of ability at mathematics. Of course, we can't be sure if your problem is mere ignorance, or drugs, or just enthusiasm.

But, Tan1.2986111111 = 0.01227 (rounded.)

What you're talking about here is the arctangent, AKA inverse tangent.

originally posted by: Ahatmose
now would you care to explain why all published reports place the angle at 51°50'35 and as a matter of fact almost all numbers quoted in Lehner's "book" have wrong angles from the given data yet no one bothers to check and those that do never bring it up. Actually all of Egyptology is like that.

Offhand, I'd guess that it is because Lehner's angle is the angle measured by surveying equipment, while yours is based on estimated (and rounded) length measurements. Again, that's just a guess.

Harte

originally posted by: Blackmarketeer
a reply to: Ahatmose

Could you enlighten us to the evidence that they are copies from 2000 BC ?

EGYPTIAN MATHEMATICS PAPYRI (and contents exhibited) (buffalo.edu)

The Rhind Papyrus (also called the Ahmes Papyrus) is named after the British collector, Rhind, who acquired it in 1858. It was copied by a scribe, Ahmes (or Ahmos), (~1650 BC) from another document written ~2000 BC, which, possibly in turn, was copied from a document from ~2650 BC (the time of Imhotep?). The Rhind Papyrus is located in the British Museum, and contains mathematics problems and solutions. All the problems below are translations.

Here we see the dating goes back even further, possibly to the very time of Khufu himself. How is that for relevant, slick? The scribe himself (Ahmes) declares it is a copy of a text from 2 centuries earlier. (source)

And: Papyruses, Mathematical (dictionary.com)

Papyruses, Mathematical

extant mathematical works of ancient Egypt, dating from the period of the Middle Kingdom (c. 21st century to c. 18th century B.C.). The most famous are the Rhind Papyrus, now in the British Museum (London), and the Moscow Papyrus, now in the A. S. Pushkin Museum of Fine Arts (Moscow).

The Rhind Papyrus, named after its owner, the Egyptologist H. Rhind, was first studied and published in German by A. Eisenlohr; it is also called the Ahmes Papyrus, after its compiler, the scribe Ahmes (c. 2000 B.C.)

 

None of the mathematical papyrus from Egypt ever - EVER - demonstrated a working formula for calculating Pi as a ratio between circumference and diameter. They only got as far as approximating a circle's area by the "method of squares" shown earlier.

The Ahmes papyrus states it is a: "thorough study of all things, insight into all that exists, knowledge of all obscure secrets." - Odd, don't you think, it would completely omit something as groundbreaking as the concept of Pi (or Phi, or Trigonometry, and so on...)

Another method devised is to approximate a circle by overlaying a 3x3 grid on it and constructing an octagon and determining the area of the octagon in place of the circle. Crude, but workable.

Now ask yourself, if Pi was so fundamental to making the Great Pyramid, and the GP was a part of the Giza "solar model" as you claim, then why are Khafre's and Menkaure's pyramids not also make using Pi? Why do their slopes diifer? Khafre used a seked of 7:5 versus Khufu's 7:5-1/2 and Menkaure used 7:5-3/5.

First thank you for those quotes. I had never seen them before. However exactly how would the scribe know they were an exact copy of a document from two centuries before unless he had that document in from of him and was totally confident of the date and exactly how would he have verified this date ? Regardless the quotes were interesting. However why is Egyptology totally full of guess work like the following statement ... "which, possibly in turn, was copied from a document from ~2650 BC" No offense but I don't think I have ever read anything from Egyptology that doesn't have several of these "probablies' in them. However it is to Meidum that we need to journey to possibly tie it all together. Some on this board have totally refused to accept a 9 by 11 ratio at Giza but that is not an isolated instance. case in point ... The perimeter of the base of Meidum is 1100.00 cubits and if one takes a very quick look at The Bent Pyramid we see a possible 9 by 11 correlation quite easily. Click on image for a larger view

However as interesting as this is I took a closer look at this diagram and it yielded something interesting.



The perimeter of the square is of course 12 units so that is no good but the octagon is (sq rt of 2 x 4) + 4 = 9.65685 while the circumference of the circle is 3 x Pi or 9.42478 for an accuracy of 0.976 - not very impressive HOWEVER let's try this if we take a circumference of 12 or one that is equal to the red sqaure we get this 12 / 2 / Pi = 1.90985932

Now I have shown that the ratio between Earth's distance from The Sun (149,598,261 km) and the distance between Earth and Mars (78340839) is equal to a ratio of 1:1.90958206 accuracy rating of 1.90958206 / 1.90985932 = 0.99986 and also the ratio of a volume of a sphere to a cube is:

volume of cube:volume of sphere=(4Pi/3)(1/2x)^3 : x^3

(pi/6)x^3:x^3
answer is pi:6
or pi/6

Reverse it and 6 / pi = 1.9098593 exactly the same as the radius in a circumference of 12.

So ratio of a cube to a sphere is simply the radius of a circle with circumference of 12

AND PLEASE REMEMBER THE RATIO OF THE METER (39.37 inches) TO THE CUBIT (20.62 inches at Giza) IS 1.90931135

1.90931135 / 1.90985932 = 0.9997

Here is a chart of the measurement at Meidum which I put together after finding Petrie's book online:



Pretty obvious I am sure to even the posters on this thread that base was 11 and height was 7 units of 25 cubits. Or is it so obvious. Petrie seemed to feel that it showed Pi just as he thought The Great Pyramid showed Pi. Here is what he wrote:



And just one more note here before we take a look at the actual sizes of what is left in the layers and we see that the height in inches is 3619 inches. Now interestingly the value of 1000 x (Phi squared + 1) = 3168.03 within a single inch of what is surmised. Interesting but I think when we look at the sizes of the remaining course it might reveal a bit more.

PS: And as further proof of the all encompassing 9 by 11 theme I present this diagram. Again click for a larger image view

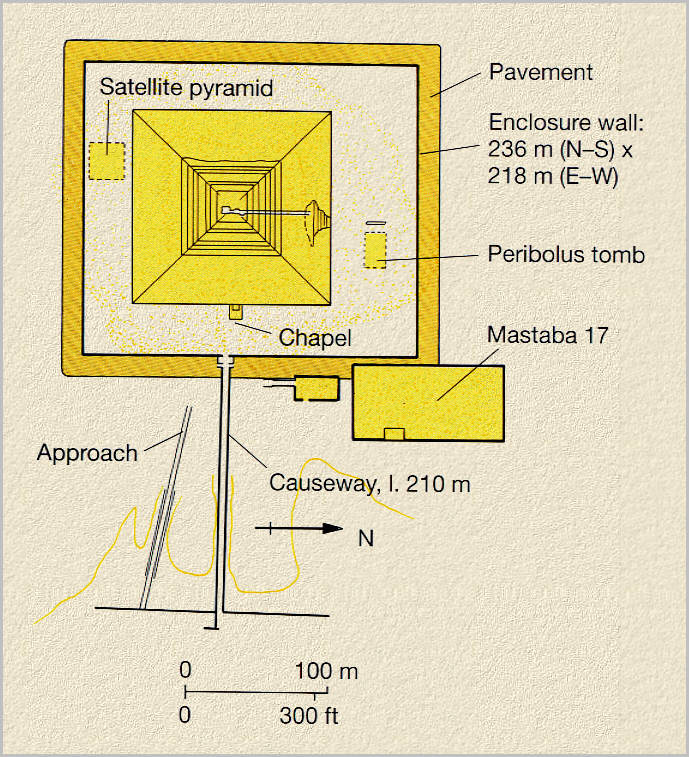
The outside wall is 236 meters = 9291.32 inches or 449.725 cubits at 20.66 inches per cubit and most probably meant to be 450 cubits even. Now the punch line and further proof of 9 by 11. The distance of 450 cubits is if we use 25 as a base unit gives us 18 or 18 x 25 = 450. The base or The Meidum Pyramid is 25 x 11 or 275 so if we take 1/2 the wall times the base and use units of 25 we do indeed have our 9 by 11 units showing up once again.

.

Your images aren't working

originally posted by: Blackmarketeer
Your images aren't working

Very weird working fine at this end. I think it is just psychosomatic and you simply don't want to see these new images.

Test image below:

a reply to: Ahatmose



This is what everyone sees. Don't bother taking a hint. If it loads for you it's likely because you already have the image cached in your browser.

Ps: I'm trying to help you so I can see these images, not trying to deny they exist..