It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
share:
Here is the same formula 48/2(9+3) typed in two calculators from Texas Instruments, the TI-85 and the TI-86, and the answers are different:

The TI-85 gives the answer as 2.
The TI-86 gives the answer as 288.
This topic was debated by a number of people and apparently about half the people got 2 and half the people got 288.
Pretty much everyone agrees that the expression could benefit from parentheses to clarify it, which depending on how the parentheses were applied would give you one answer or the other.
I did a little research into this to see if there really is a right answer and thought I'd post a few things I found that might be of interest.
If you found this expression in a journal published by the American Physical Society, the expression is not ambiguous and has a defined value. Here is the convention used for manuscripts submitted for publication in their journals:
Physical Review Style and Notation Guide (pdf) p21

That convention is prominent in physics in other literature like prominent physics textbooks:
Order of operations
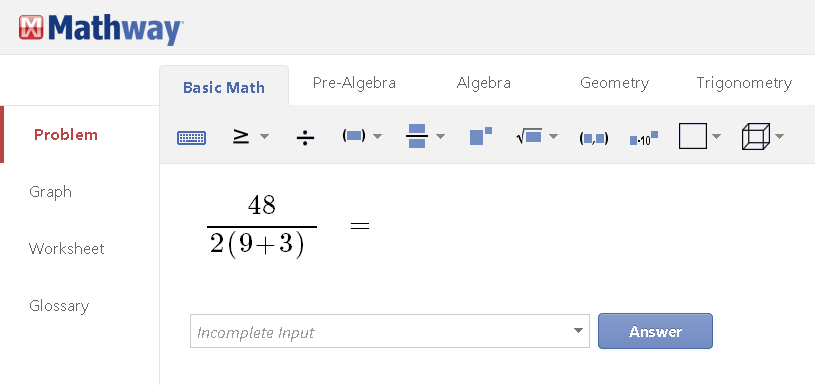
I find it hard to interpret the expression differently from how it displays in that mathway screenshot, because of the bias in the physics textbooks since physics was one of my majors. To put it another way, if you wanted the term (9+3) to be part of the numerator, why not write it to the left of the slash symbol, so the expression then becomes: (9+3)48/2 or 48(9+3)/2, which again using the convention in APS journals and prominent physics texts gives you the unambiguous answer of 288.
There is another interpretation which is pretty common that states the answer is 2, based on the implied multiplication having priority over explicit multiplication issue mentioned in the quote above regarding a change in 2013 in Wolfram Alpha. I couldn't find much documentation on this, but one reason it's not even an issue at the American Physical Society is, they don't even use multiplication signs for multiplication, rather they are used only for vector products so all multiplication is the "implied" type:
48/2(9+3) - implied
48/2x(9+3) - explicit
This can make a difference in some calculators:

The answer is 2 when implied multiplication takes priority, and 288 when the multiplication is explicit and not implied.
I did find out some things about how and why people interpret it differently, and I think there are some misconceptions, which I'll mention here, by some acronyms:
There is some confusion about PEMDAS that M coming before D implies it's consistent with the APR journal standards potting a higher priority on multiplication than Division, but for some reason, the proponents of this mnemonic have chosen not to resolve such ambiguity and say that M coming before D actually doesn't imply M has a higher priority (maybe it should, but it doesn't).
Further, I found that some people have this "left to right" mentality about the order in which operations should be performed, but I don't think this is a sign of clear thinking and may be a sign of a fault in the educational system, as explained here by someone who has given this subject a lot of thought:
“Order of operations” and other oddities in school mathematics
So in conclusion, we can't say that either 2 or 288 is the wrong answer. However if you're following prominent physics textbooks or reading journals from the American Physical Society, if you said the answer is 2, you would be right, because of the conventions followed in those sources. One reason you may want to adopt such convention yourself even if you're not a student of physics is that you will confuse yourself less often if you follow an unambiguous convention (like expressions to the left of the slash are the numerator and expressions to the right of the slash are the denominator). Or if all that school stuff is behind you, maybe this can help your children if they are still in school, since the author of the "school mathematics" source above points out we are probably not doing the best job we can of educating our children.
If you want to run this by your kids to see if they know the answer, it would be interesting to see if they even notice it's ambiguous (unless they started studying physics in which case it might not be as ambiguous, depending on what textbook they use).

The TI-85 gives the answer as 2.
The TI-86 gives the answer as 288.

This topic was debated by a number of people and apparently about half the people got 2 and half the people got 288.
Pretty much everyone agrees that the expression could benefit from parentheses to clarify it, which depending on how the parentheses were applied would give you one answer or the other.
I did a little research into this to see if there really is a right answer and thought I'd post a few things I found that might be of interest.
If you found this expression in a journal published by the American Physical Society, the expression is not ambiguous and has a defined value. Here is the convention used for manuscripts submitted for publication in their journals:
Physical Review Style and Notation Guide (pdf) p21

That convention is prominent in physics in other literature like prominent physics textbooks:
Order of operations
I am postulating that one reason they may teach physics students an unambiguous interpretation is to get them thinking about how to write expressions clearly. In this context, when you see the slash as a "divide by" symbol, what appears to the left of the slash is the numerator, and what appears to the right of the slash is the denominator. When I typed the formula into Mathway, it interpreted and displayed the formula as such:
the manuscript submission instructions for the Physical Review journals state that multiplication is of higher precedence than division with a slash, and this is also the convention observed in prominent physics textbooks such as the Course of Theoretical Physics by Landau and Lif#z and the Feynman Lectures on Physics. Wolfram Alpha changed in early 2013 to treat implied multiplication the same as explicit multiplication (formerly, implied multiplication without parentheses was assumed to bind stronger than explicit multiplication).

I find it hard to interpret the expression differently from how it displays in that mathway screenshot, because of the bias in the physics textbooks since physics was one of my majors. To put it another way, if you wanted the term (9+3) to be part of the numerator, why not write it to the left of the slash symbol, so the expression then becomes: (9+3)48/2 or 48(9+3)/2, which again using the convention in APS journals and prominent physics texts gives you the unambiguous answer of 288.
There is another interpretation which is pretty common that states the answer is 2, based on the implied multiplication having priority over explicit multiplication issue mentioned in the quote above regarding a change in 2013 in Wolfram Alpha. I couldn't find much documentation on this, but one reason it's not even an issue at the American Physical Society is, they don't even use multiplication signs for multiplication, rather they are used only for vector products so all multiplication is the "implied" type:
48/2(9+3) - implied
48/2x(9+3) - explicit
This can make a difference in some calculators:

The answer is 2 when implied multiplication takes priority, and 288 when the multiplication is explicit and not implied.
I did find out some things about how and why people interpret it differently, and I think there are some misconceptions, which I'll mention here, by some acronyms:
In this context, the "O" in BOMDAS means "Order" and is referring to exponents or powers, not the order in which terms appear, and there seems to be some confusion about that which I'll come to shortly.
PEMDAS is common. It stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. PEMDAS is often expanded to "Please Excuse My Dear Aunt Sally" with the first letter of each word creating the acronym PEMDAS. Canada uses BEDMAS. It stands for Brackets, Exponents, Division, Multiplication, Addition, Subtraction...Since multiplication and division are of equal precedence, M and D are often interchanged, leading to such acronyms as BOMDAS.
There is some confusion about PEMDAS that M coming before D implies it's consistent with the APR journal standards potting a higher priority on multiplication than Division, but for some reason, the proponents of this mnemonic have chosen not to resolve such ambiguity and say that M coming before D actually doesn't imply M has a higher priority (maybe it should, but it doesn't).
Further, I found that some people have this "left to right" mentality about the order in which operations should be performed, but I don't think this is a sign of clear thinking and may be a sign of a fault in the educational system, as explained here by someone who has given this subject a lot of thought:
“Order of operations” and other oddities in school mathematics
However this idea of left to right is actually extraneous, but at least now I understand why so many people have this extraneous idea, because that's what they were taught:
An example is the convention known as the Rules for the Order of Operations, introduced into the school curriculum in the fifth or sixth grade:
(1) Evaluate all expressions with exponents.
(2) Multiply and divide in order from left to right.
(3) Add and subtract in order from left to right.
In short, these rules dictate that, to carry out the computations of an arithmetic expression, evaluate the exponents first, then multiplications and divisions, then additions and subtractions, and always from left to right
(B) exponents first, then multiplications and divisions, then additions and
subtractions.
Except for the stipulation about performing the operations “from left to right”, (B) is seen to be exactly the same as the Rules for the Order of Operations. It is important to note that this stipulation about “from left to right” is entirely extraneous, because the associative laws of addition and multiplication ensure that it makes no difference whatsoever in what order the additions or multiplications are carried out.
So in conclusion, we can't say that either 2 or 288 is the wrong answer. However if you're following prominent physics textbooks or reading journals from the American Physical Society, if you said the answer is 2, you would be right, because of the conventions followed in those sources. One reason you may want to adopt such convention yourself even if you're not a student of physics is that you will confuse yourself less often if you follow an unambiguous convention (like expressions to the left of the slash are the numerator and expressions to the right of the slash are the denominator). Or if all that school stuff is behind you, maybe this can help your children if they are still in school, since the author of the "school mathematics" source above points out we are probably not doing the best job we can of educating our children.
If you want to run this by your kids to see if they know the answer, it would be interesting to see if they even notice it's ambiguous (unless they started studying physics in which case it might not be as ambiguous, depending on what textbook they use).
reply to post by Arbitrageur
Ahh the old TI 85 vs TI 86 conspiracy. Btw, you really have way too much time on your hands.
Ahh the old TI 85 vs TI 86 conspiracy. Btw, you really have way too much time on your hands.
reply to post by Arbitrageur
while opening a business once, we were managing preopening purchases of around 1.2mil. this was everything needed to run the business from soup to nuts.
So while we are laying out our "OSE" budget, we break everything down by department, then within the departmnts we classify the items by type (in line with the conventional 10th edition uniform code of accounts book). So we have a workbook with several tabs, each tab with the same info (columns for vendor, classification of the item, unit count, unit cost, etc).
There are also calculated cells so that I can layer in a 10% shipping/handling fee, and the standard sales and use tax. It calculates by item, then calculates the sum.
While going through this exciting exercise with a coworker, we noticed that when you add it up using a calculator, we had about 5k in total variance from that 1.2mil total.
The reason, we found, has to do with the programming that performs the math in the calculator is different than what we have in our computer powering our spreadsheet. My spreadsheets balanced perfectly to the invoices, so the calculator was what was inaccurate.
while opening a business once, we were managing preopening purchases of around 1.2mil. this was everything needed to run the business from soup to nuts.
So while we are laying out our "OSE" budget, we break everything down by department, then within the departmnts we classify the items by type (in line with the conventional 10th edition uniform code of accounts book). So we have a workbook with several tabs, each tab with the same info (columns for vendor, classification of the item, unit count, unit cost, etc).
There are also calculated cells so that I can layer in a 10% shipping/handling fee, and the standard sales and use tax. It calculates by item, then calculates the sum.
While going through this exciting exercise with a coworker, we noticed that when you add it up using a calculator, we had about 5k in total variance from that 1.2mil total.
The reason, we found, has to do with the programming that performs the math in the calculator is different than what we have in our computer powering our spreadsheet. My spreadsheets balanced perfectly to the invoices, so the calculator was what was inaccurate.
reply to post by bigfatfurrytexan
That's interesting, that the calculator was apparently wrong.
One other thing I ran across is that Microsoft Excel does some "wrong" things too, in opposition to certain conventions which are accepted. For example, Excel doesn't handle nested exponents in the generally accepted ways, and the answers in Excel can be considerably off as a result. So, you have to be real careful when using Excel.
That's interesting, that the calculator was apparently wrong.
One other thing I ran across is that Microsoft Excel does some "wrong" things too, in opposition to certain conventions which are accepted. For example, Excel doesn't handle nested exponents in the generally accepted ways, and the answers in Excel can be considerably off as a result. So, you have to be real careful when using Excel.
Not enough time apparently, because I was wondering if the illuminati had something to do with it but I didn't have time to look into that.
doorhandle
reply to post by Arbitrageur
Ahh the old TI 85 vs TI 86 conspiracy. Btw, you really have way too much time on your hands.
Seriously though, I'm more curious about why Wolfram Alpha changed the answer, but not curious enough to ask them.
Arbitrageur
reply to post by bigfatfurrytexan
That's interesting, that the calculator was apparently wrong.
One other thing I ran across is that Microsoft Excel does some "wrong" things too, in opposition to certain conventions which are accepted. For example, Excel doesn't handle nested exponents in the generally accepted ways, and the answers in Excel can be considerably off as a result. So, you have to be real careful when using Excel.
For accounting, it is ideal. Macroeconomics....you need a solid database. I've never considered using it for anything other than business statistics and accounting.
reply to post by Arbitrageur
I got two in my head, but yeah it's pretty standard when using TI to calculate to insert enough parentheses to create your own order of operations
I got two in my head, but yeah it's pretty standard when using TI to calculate to insert enough parentheses to create your own order of operations
edit on 28-2-2014 by slunteri because: (no reason given)
we were taught pemdas in school
Parentheses
Exponent
Multiply
Divide
Addition
Subtraction
that would be the proper way to do the math equation.
Parentheses
Exponent
Multiply
Divide
Addition
Subtraction
that would be the proper way to do the math equation.
PHP will yield 288. It seems after doing the addition in the parens, it processes left to right with the mults and divs giving them the same level of
precedence.
Edit:
Which is how it is documented.
Edit:
Which is how it is documented.
edit on 2/28/2014 by roadgravel because: additional comment
reply to post by Arbitrageur
The general accepted rules of mathematics Multiplication, Division, addition and subtraction is that it occurs in that order. Therefore /2 operand takes place before 9+3.
The general accepted rules of mathematics Multiplication, Division, addition and subtraction is that it occurs in that order. Therefore /2 operand takes place before 9+3.
Aren't the operations in the parens processed first. That is why complex formulas are best done with parens to generate the correct output.
reply to post by roadgravel
yeh they are, but that doesn't override 48/2 ....its not 48/(9+3) first.
yeh they are, but that doesn't override 48/2 ....its not 48/(9+3) first.
Well, I got 288... but any other # could be correct depending on the variables of the equation, or as I would put it, it depends on which rules need
to be applied to achieve the result you are looking for.
The problem imo is using / which means divide, as a divider between num and denom
Calculators should have a separate symbol for compound fractions than the divide sign ( i thought some did?)
Calculators should have a separate symbol for compound fractions than the divide sign ( i thought some did?)
But it's not due to the + sign, the parens override that. It's the implied multiplication of the 12 caused by the parens.
reply to post by roadgravel
I have never heard them referred to as parens. I Googled it, and it appears correct, but it seems odd. Is it a regional thing, just easier to type or is it the fancy pants way?
Anyway I got 288.
Knowyourmeme article on this actually breaks it down fairly well.
I have never heard them referred to as parens. I Googled it, and it appears correct, but it seems odd. Is it a regional thing, just easier to type or is it the fancy pants way?
Anyway I got 288.
Knowyourmeme article on this actually breaks it down fairly well.
reply to post by Domo1
just a short way of saying the longer word. I suppose it's a programmer thing. Like saying dot instead of period.
just a short way of saying the longer word. I suppose it's a programmer thing. Like saying dot instead of period.
If you need a calculator do that equation then you deserve to be mislead!
They just didn't make the terms multiply when there is no operator in between them. Read the manual!
They just didn't make the terms multiply when there is no operator in between them. Read the manual!
It's accepted by some, but not universally, but why it's not more accepted I don't know. I I think it would be a good thing if it was. But since the 9+3 is in parentheses, that gets added to 12 before anything else.
AthlonSavage
reply to post by Arbitrageur
The general accepted rules of mathematics Multiplication, Division, addition and subtraction is that it occurs in that order. Therefore /2 operand takes place before 9+3.
Then you are left with 48/2(12) and if we follow your order of multiplication before division, 2 multiplied by 12 would happen first, then the division, right? So the result is 48/24.
It's 48/2(12)
AthlonSavage
reply to post by roadgravel
yeh they are, but that doesn't override 48/2 ....its not 48/(9+3) first.
new topics
-
Russian intelligence officer: explosions at defense factories in the USA and Wales may be sabotage
Weaponry: 1 hours ago -
African "Newcomers" Tell NYC They Don't Like the Free Food or Shelter They've Been Given
Social Issues and Civil Unrest: 2 hours ago -
Russia Flooding
Other Current Events: 4 hours ago -
MULTIPLE SKYMASTER MESSAGES GOING OUT
World War Three: 4 hours ago -
Two Serious Crimes Committed by President JOE BIDEN that are Easy to Impeach Him For.
US Political Madness: 5 hours ago -
911 emergency lines are DOWN across multiple states
Breaking Alternative News: 5 hours ago -
Former NYT Reporter Attacks Scientists For Misleading Him Over COVID Lab-Leak Theory
Education and Media: 7 hours ago -
Why did Phizer team with nanobot maker
Medical Issues & Conspiracies: 7 hours ago -
Pro Hamas protesters at Columbia claim hit with chemical spray
World War Three: 8 hours ago -
Elites disapearing
Political Conspiracies: 10 hours ago
top topics
-
Go Woke, Go Broke--Forbes Confirms Disney Has Lost Money On Star Wars
Movies: 12 hours ago, 13 flags -
Pro Hamas protesters at Columbia claim hit with chemical spray
World War Three: 8 hours ago, 11 flags -
Elites disapearing
Political Conspiracies: 10 hours ago, 9 flags -
Freddie Mercury
Paranormal Studies: 12 hours ago, 7 flags -
Nirvana - Immigrant Song
Music: 17 hours ago, 5 flags -
A Personal Cigar UFO/UAP Video footage I have held onto and will release it here and now.
Aliens and UFOs: 10 hours ago, 5 flags -
African "Newcomers" Tell NYC They Don't Like the Free Food or Shelter They've Been Given
Social Issues and Civil Unrest: 2 hours ago, 5 flags -
Two Serious Crimes Committed by President JOE BIDEN that are Easy to Impeach Him For.
US Political Madness: 5 hours ago, 5 flags -
911 emergency lines are DOWN across multiple states
Breaking Alternative News: 5 hours ago, 4 flags -
Former NYT Reporter Attacks Scientists For Misleading Him Over COVID Lab-Leak Theory
Education and Media: 7 hours ago, 4 flags
active topics
-
I Guess Cloud Seeding Works
Fragile Earth • 21 • : BrucellaOrchitis -
Elites disapearing
Political Conspiracies • 20 • : HerbertWest -
What Time is it on the Moon ?
Space Exploration • 50 • : wildespace2 -
Russian intelligence officer: explosions at defense factories in the USA and Wales may be sabotage
Weaponry • 18 • : Lazy88 -
Why did Phizer team with nanobot maker
Medical Issues & Conspiracies • 6 • : annonentity -
Israel ufo shoot down drones?
Aliens and UFOs • 26 • : GENERAL EYES -
African "Newcomers" Tell NYC They Don't Like the Free Food or Shelter They've Been Given
Social Issues and Civil Unrest • 4 • : GENERAL EYES -
The Acronym Game .. Pt.3
General Chit Chat • 7722 • : bally001 -
Two Serious Crimes Committed by President JOE BIDEN that are Easy to Impeach Him For.
US Political Madness • 7 • : Disgusted123 -
Russia Flooding
Other Current Events • 1 • : ksihkahe
