It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
share:
Time - Energy Equivalence
by John SkieSwanne
What is time? We can walk backward in space, but never backward in time. It's the great mystery, which prevents us to reach the past.
But... recently I noticed something which I wanted to share with you so that the mystery might start to clear up. I noticed that Time is not only related to distance and speed... but also might be equivalent (not just related) to energy and mass.
Mass-energy equivalence has been discovered by Albert Einstein in 1905, and it goes as such:
E=mc^2
Which happens to be the most popular equation ever. To those investigative minds who may doubt the equation's validity, I must insist that this equation can be verified to be true. Merging it with Planck's equation give a modified version of DeBroglie's equation, which accurately predicts that electron-positron annihilation will give off gamma radiation.
Now, I've noticed that there is a hidden Time component in Einstein's "E=mc^2" equation. I figured that it was possible to reverse this famous equation so that instead of showing mass-energy equivalence, the equation gives time-energy equivalence (or time-mass equivalence) instead.
The "c" component represents a very specific, fixed speed: light speed (299,792,498 meters per second). As you know, speed is, in fact, reducible to two components: distance divided by time.
In "c^2", only the distance is squared, not the time component. By this I mean that for instance, if "A" would represent "5 meters covered each 1 second", then "A^2" becomes "25 meters covered in 1 second", and not "25 meters covered in 5 seconds".
For the sake of simplicity, let's pretend for an instant that there's an exotic length unit which some planet around Vega uses, and it's called a "Joua", and 1 Joua is exactly equal to 59958491.6 of our meters. In this exotic scale, light speed would be equal to 5 Joua per 1 second.
Now all you have to do is take a pen and a paper to compute the inversion of Einstein's equation:
If there's a mass of 3 kilograms, and if the square of 5 Joua per second is equal to 25 Joua per 1 second, then Energy will be equal to 3*((5^2)/1), or 3*(25). In other words, 75.
E=mc^2
E=m*(the square of 5 joua / 1 second)
E=m*(25 joua / 1 second)
E=m*(25/1)
E=m*(25)
E=3*25
75=3*25
Now let us reverse this.
Let's deduce: What is c^2 equal to? If 75 is equal to 3 multiplied by 25 (75=3*25), then 25 can only be equal to 75 divided by 3 (25=75/3). Which means the first thing we are going to do is couple the energy component with the mass component:
c^2=E/m
But that's not all. Notice the square (^2) component. To have the pure light speed component, we have to separate "c" from its square. but c (5 joua per 1 second) can't equal 25 on its own, unless the 25 is squareroot-ed.
c=sqrt(E/m)
Now all that's left for us to do is to separate Time from the c component. We know that Time is equal here to 1 second. But 1 cannot give 5 on its own. Which means, 5 must be divided by another 5, which happens to be the value of the distance component:
T=d/(sqrt(E/m))
So now, without further delay, ladies and gentlemen, I present to you, the Time-energy (or time-mass) equivalence equation:
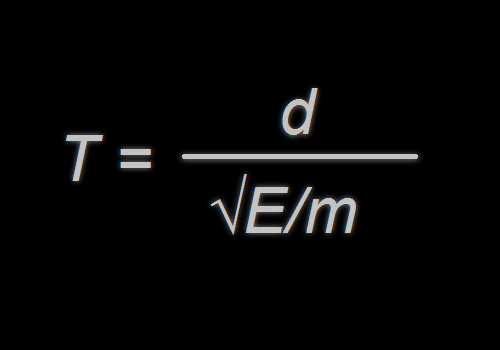
Where d is the distance, equal to 299,792,498 meters.
In the past, I often wondered if Time was not a force by itself. Today I learned this is not true, but yet, I can't help but notice how Time is dependent upon distance, like any other forces...
Anyway. This equation does predict something quite interesting, though - check this out:
If mass of the opposite sign should exist, such as the one predicted by Dragan Hajdukovic's theory, then its equivalent time would stop being positive. According to current mathematics, Time wouldn't even become negative. It would become un-real. Literally. The equation will include an imaginary number, and the resulting Time value will be a non-real number. This may imply that Dragan's gravitational dipoles cannot exist in "real" time; or it may imply that gravitational fields of the opposite sign (if such thing exists at all) have Time which is quite anomalous (and quite interesting, too!).
Anyway, so this Time-energy equivalence equation is what I recently found out. I don't know what to make of it yet - I'm only scratching the surface. What say you?
At Time's End,
Swan
by John SkieSwanne
What is time? We can walk backward in space, but never backward in time. It's the great mystery, which prevents us to reach the past.
But... recently I noticed something which I wanted to share with you so that the mystery might start to clear up. I noticed that Time is not only related to distance and speed... but also might be equivalent (not just related) to energy and mass.
Mass-energy equivalence has been discovered by Albert Einstein in 1905, and it goes as such:
E=mc^2
Which happens to be the most popular equation ever. To those investigative minds who may doubt the equation's validity, I must insist that this equation can be verified to be true. Merging it with Planck's equation give a modified version of DeBroglie's equation, which accurately predicts that electron-positron annihilation will give off gamma radiation.
Now, I've noticed that there is a hidden Time component in Einstein's "E=mc^2" equation. I figured that it was possible to reverse this famous equation so that instead of showing mass-energy equivalence, the equation gives time-energy equivalence (or time-mass equivalence) instead.
The "c" component represents a very specific, fixed speed: light speed (299,792,498 meters per second). As you know, speed is, in fact, reducible to two components: distance divided by time.
In "c^2", only the distance is squared, not the time component. By this I mean that for instance, if "A" would represent "5 meters covered each 1 second", then "A^2" becomes "25 meters covered in 1 second", and not "25 meters covered in 5 seconds".
For the sake of simplicity, let's pretend for an instant that there's an exotic length unit which some planet around Vega uses, and it's called a "Joua", and 1 Joua is exactly equal to 59958491.6 of our meters. In this exotic scale, light speed would be equal to 5 Joua per 1 second.
Now all you have to do is take a pen and a paper to compute the inversion of Einstein's equation:
If there's a mass of 3 kilograms, and if the square of 5 Joua per second is equal to 25 Joua per 1 second, then Energy will be equal to 3*((5^2)/1), or 3*(25). In other words, 75.
E=mc^2
E=m*(the square of 5 joua / 1 second)
E=m*(25 joua / 1 second)
E=m*(25/1)
E=m*(25)
E=3*25
75=3*25
Now let us reverse this.
Let's deduce: What is c^2 equal to? If 75 is equal to 3 multiplied by 25 (75=3*25), then 25 can only be equal to 75 divided by 3 (25=75/3). Which means the first thing we are going to do is couple the energy component with the mass component:
c^2=E/m
But that's not all. Notice the square (^2) component. To have the pure light speed component, we have to separate "c" from its square. but c (5 joua per 1 second) can't equal 25 on its own, unless the 25 is squareroot-ed.
c=sqrt(E/m)
Now all that's left for us to do is to separate Time from the c component. We know that Time is equal here to 1 second. But 1 cannot give 5 on its own. Which means, 5 must be divided by another 5, which happens to be the value of the distance component:
T=d/(sqrt(E/m))
So now, without further delay, ladies and gentlemen, I present to you, the Time-energy (or time-mass) equivalence equation:
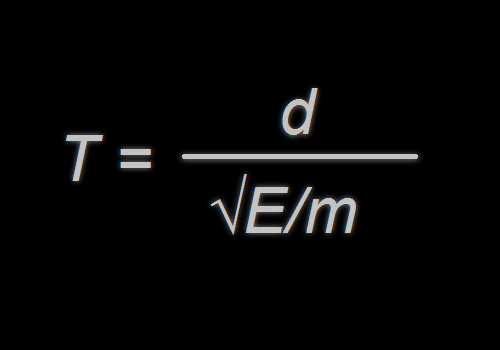
Where d is the distance, equal to 299,792,498 meters.
In the past, I often wondered if Time was not a force by itself. Today I learned this is not true, but yet, I can't help but notice how Time is dependent upon distance, like any other forces...
Anyway. This equation does predict something quite interesting, though - check this out:
If mass of the opposite sign should exist, such as the one predicted by Dragan Hajdukovic's theory, then its equivalent time would stop being positive. According to current mathematics, Time wouldn't even become negative. It would become un-real. Literally. The equation will include an imaginary number, and the resulting Time value will be a non-real number. This may imply that Dragan's gravitational dipoles cannot exist in "real" time; or it may imply that gravitational fields of the opposite sign (if such thing exists at all) have Time which is quite anomalous (and quite interesting, too!).
Anyway, so this Time-energy equivalence equation is what I recently found out. I don't know what to make of it yet - I'm only scratching the surface. What say you?
At Time's End,
Swan
reply to post by swanne
Time is simply a measurement of how long it takes entropy to occur. But does it follow a linear path? I strongly suspect otherwise.
Time is simply a measurement of how long it takes entropy to occur. But does it follow a linear path? I strongly suspect otherwise.
edit on
26-12-2013 by andy06shake because: (no reason given)
This is an extremely basic concept I have about time, that it is simply motion, which is energy.
Atoms and molecules are in motion even when an object is motionless (of course nothing is motionless).
Kinetic energy is motion which is equivalent to time.
Just my basic thoughts on time.
Atoms and molecules are in motion even when an object is motionless (of course nothing is motionless).
Kinetic energy is motion which is equivalent to time.
Just my basic thoughts on time.
reply to post by swanne
Okay Swan - I have never seen that before. When you said "There is a hidden time component in e = mc^2, I said "Well, where is it?" and then you mentioned "c" and I immediately said, "Oh my God he's right..."
I'm going to look these over.
Imaginary time. Interesting. I've been wondering about imaginary numbers representing another dimension in the normal x-y-z graphs. I have also been wondering about using imaginary numbers in order to explain more about Godel's Incompleteness Theorem and Set Theory -
So I was thinking that if the system of natural numbers was multi-dimensional, you might need to use imaginary numbers in order to prove the relationships between the natural numbers.
Okay Swan - I have never seen that before. When you said "There is a hidden time component in e = mc^2, I said "Well, where is it?" and then you mentioned "c" and I immediately said, "Oh my God he's right..."
I'm going to look these over.
Imaginary time. Interesting. I've been wondering about imaginary numbers representing another dimension in the normal x-y-z graphs. I have also been wondering about using imaginary numbers in order to explain more about Godel's Incompleteness Theorem and Set Theory -
The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an "effective procedure" (e.g., a computer program, but it could be any sort of algorithm) is capable of proving all truths about the relations of the natural numbers (arithmetic). For any such system, there will always be statements about the natural numbers that are true, but that are unprovable within the system. The second incompleteness theorem, an extension of the first, shows that such a system cannot demonstrate its own consistency.
So I was thinking that if the system of natural numbers was multi-dimensional, you might need to use imaginary numbers in order to prove the relationships between the natural numbers.
edit on 26amThu, 26 Dec 2013 09:26:13 -0600kbamkAmerica/Chicago by darkbake because: (no reason given)
MichiganSwampBuck
Kinetic energy is motion which is equivalent to time.
ke = (1/2)*mv^2
(2*ke)/m = v^2
Root((2*ke)/m) = v
v = meters / second
Okay O.P. - how did you go about ripping the seconds out of that m /s again? Oh... you just called meters "d"...
(Root((2*ke)/m))/d = t
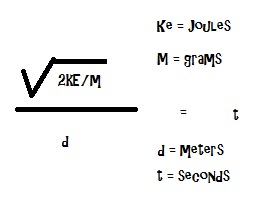
In my equation as well, you can get imaginary time from a negative mass...
Oh... check this out! If your Ke = 2 joules, m = 1 gram, d = 1 meter, then you travel for 2 seconds!
Okay... so if your ke = -2 joules, and your m = 1 gram, d = 1 meter, you travel for 2i seconds...
That's assuming you are using some kind of machine that is made of matter.
Or, you could have an anti-matter machine and that takes out the need for the anti-energy... and then:
ke = 2 joules, m = -1 gram, d = 1 meter, you travel for 2i seconds.
When people speak of anti-matter, it's important to recognize that anti-matter isn't some sort of 'negative' matter. An anti-particle is just as real as any other particle. If you use Einstein's famous E=mc2 relation you find that an anti-particle has positive energy, since it has a mass which is identical to the mass of its partner 'particle.' The 'anti-' part of the name just signifies the fact that the quantum numbers that the particle has are opposite of those of the corresponding particle.
PhysLink.com
Okay. So at this point since anti-matter is defined by quantum numbers I might have to delve into diagrams of this at some point (I do things pictorially) in order to come to any other conclusions.
Although a lot of times cool stuff is overlooked in the pictorial representations of advanced formulas! I think it is because no one takes them seriously.
Saving this thread. S&F.
edit on 26amThu, 26 Dec 2013 09:45:42 -0600kbamkAmerica/Chicago by darkbake because: (no reason
given)
edit on 26amThu, 26 Dec 2013 09:55:22 -0600kbamkAmerica/Chicago by darkbake because: (no reason given)
reply to post by swanne
Good food for thought, but I noticed an error in your logic.
Numerical calculations mean nothing without corresponding units. 75 what? It wouldn't be 75 Joules, since the Joule is a unit tied to the gram, meter, second, etc. It would be 75 "somethings," with "something" being another assumed measurement.
The end result would be the same, because the physical laws that connect the units in a measurement system are constant.
Still, t = d / √(E/m) intrigues me for some reason.
Also:
Incorrect. If c is in the units of m/s, then c² is in the units of m²/s². Somehow you managed to come up with an accurate final equation despite this.
I have no idea what you are doing here, but again, it appears you have the final equation correct. It appears you are attempting to introduce a constant into the equation, which never quite made it.
I would also like to point out one final thing:
We can only walk backwards in space if we assign an arbitrary direction to the term "forward." One can look at any movement in space as forward simply by adjusting that convention. Velocity in space is usually considered a positive scalar component of the vector describing the motion in space.
The same can be thought of when considering time. Is it possible that we are going "backwards" in time already? Absolutely, if one assumes the forward direction to be the opposite of our direction. In reality, however, that assumption of positive direction is meaningless outside the context of the specific equations it is used in, since either assumption will give the same final result.
TheRedneck
Good food for thought, but I noticed an error in your logic.
If there's a mass of 3 kilograms, and if the square of 5 Joua per second is equal to 25 Joua per 1 second, then Energy will be equal to 3*((5^2)/1), or 3*(25). In other words, 75.
Numerical calculations mean nothing without corresponding units. 75 what? It wouldn't be 75 Joules, since the Joule is a unit tied to the gram, meter, second, etc. It would be 75 "somethings," with "something" being another assumed measurement.
The end result would be the same, because the physical laws that connect the units in a measurement system are constant.
Still, t = d / √(E/m) intrigues me for some reason.
Also:
In "c^2", only the distance is squared, not the time component. By this I mean that for instance, if "A" would represent "5 meters covered each 1 second", then "A^2" becomes "25 meters covered in 1 second", and not "25 meters covered in 5 seconds".
Incorrect. If c is in the units of m/s, then c² is in the units of m²/s². Somehow you managed to come up with an accurate final equation despite this.
Now all that's left for us to do is to separate Time from the c component. We know that Time is equal here to 1 second. But 1 cannot give 5 on its own. Which means, 5 must be divided by another 5, which happens to be the value of the distance component:
I have no idea what you are doing here, but again, it appears you have the final equation correct. It appears you are attempting to introduce a constant into the equation, which never quite made it.
I would also like to point out one final thing:
What is time? We can walk backward in space, but never backward in time. It's the great mystery, which prevents us to reach the past.
We can only walk backwards in space if we assign an arbitrary direction to the term "forward." One can look at any movement in space as forward simply by adjusting that convention. Velocity in space is usually considered a positive scalar component of the vector describing the motion in space.
The same can be thought of when considering time. Is it possible that we are going "backwards" in time already? Absolutely, if one assumes the forward direction to be the opposite of our direction. In reality, however, that assumption of positive direction is meaningless outside the context of the specific equations it is used in, since either assumption will give the same final result.
TheRedneck
I'm no mathematician, but it seems that time is represented by irrational numbers in many if not most cases within this equation. Unless of course the
ratio of energy to mass is a perfect square.
So like the infinite transcendental number pi, could one imagine that each infinite transcendental number generated by this equation produces a unique pattern for that instance of time, while simultaneously containing within it all information within existence or every possible finite sequence of numbers?
That is to say, each of us should exist at least by the spelling of our name and digits on a social security card, simultaneously within other infinite yet unique time-lines.
Just something to think about.
source: www.askamathematician.com... its-of-pi/
So like the infinite transcendental number pi, could one imagine that each infinite transcendental number generated by this equation produces a unique pattern for that instance of time, while simultaneously containing within it all information within existence or every possible finite sequence of numbers?
That is to say, each of us should exist at least by the spelling of our name and digits on a social security card, simultaneously within other infinite yet unique time-lines.
Just something to think about.
source: www.askamathematician.com... its-of-pi/
edit on 26-12-2013 by seasoul because: (no reason given)
Nice try, but you made a mistake. in the equation E=mc², d and t have a fixed ratio, and your equation doesn't represent that fixed ratio. So the exact point of your mistake is this:
swanne
Where d is the distance, equal to 299,792,498 meters.
You can't do that and retain the meaning of the original equation.
Now all that's left for us to do is to separate Time from the c component.
if you say that
d=299,792,498 meters then you are also saying that t=1, because of that fixed ratio, but you didn't say that and it's not shown in your equation, but it's part of the original equation.
if d=299,792,498 meters, your equation gets a 1 on the left side instead of t, and it's still just a re-arranged version of E=mc²
In the process of breaking up the constant c into what appear to be component variables, you have partly destroyed the original equation.
ETA: To put it another way, if the original equation was E=mv² where v was a variable velocity, then what you did would be fine. But c isn't a variable.
edit on 26-12-2013 by Arbitrageur because: clarification
reply to post by swanne
you made a mistake,
E = mc^2
In SI units:
J = Kg X m/s X m/s
J X s^2 = Kg X m^2
s^2 = Kg X m^2 / J
s = m X root(Kg/J)
So in order for s to be negative the root of Kg/J has to be negative OR distance has to be negative. For the root of Kg/J to be negative there has to be an imaginary component (which really means a vector at 90 degrees or 270 degrees). Mass is a scalar, unless the higgs boson uncovers a vector component which is a possibility, although unlikely. Energy is also scalar.
So. I'm afraid that unless the higgs field imparts an as yet undiscovered vector component to mass that equation will never result in negative time.
you made a mistake,
E = mc^2
In SI units:
J = Kg X m/s X m/s
J X s^2 = Kg X m^2
s^2 = Kg X m^2 / J
s = m X root(Kg/J)
So in order for s to be negative the root of Kg/J has to be negative OR distance has to be negative. For the root of Kg/J to be negative there has to be an imaginary component (which really means a vector at 90 degrees or 270 degrees). Mass is a scalar, unless the higgs boson uncovers a vector component which is a possibility, although unlikely. Energy is also scalar.
So. I'm afraid that unless the higgs field imparts an as yet undiscovered vector component to mass that equation will never result in negative time.
yorkshirelad
So. I'm afraid that unless the higgs field imparts an as yet undiscovered vector component to mass that equation will never result in negative time.
It is all very well, but please note that I never stated that the equation was capable of yielding negative time. I in fact actually agree with you: negative time cannot exist, only, at worst, imaginary time (includes imaginary number i).
In fact, my equation may perhaps, in that respect, prove how come time is always observed to be positive (aka, the arrow of time) in our universe.
edit on 26-12-2013 by swanne because: (no reason given)
Your post made me think alot, I'll spend some time thinking about it but now I'm at work.
Good point, and that's what I thought at first. But It makes no sense if one thinks about it. the square of, for instance, 2 meters per 2 seconds can't give 4 meters per 4 seconds, Because 4 meters per 4 seconds is exactly equal to 2 meters per 2 seconds. If I go at 60 miles per hour, and you'd tell me to double my speed, I would go to 120 miles per hour, not 120 miles per 2 hours (which is equal to 60 miles per hour).
Regards,
Swan
TheRedneck
Incorrect. If c is in the units of m/s, then c² is in the units of m²/s². Somehow you managed to come up with an accurate final equation despite this.
Good point, and that's what I thought at first. But It makes no sense if one thinks about it. the square of, for instance, 2 meters per 2 seconds can't give 4 meters per 4 seconds, Because 4 meters per 4 seconds is exactly equal to 2 meters per 2 seconds. If I go at 60 miles per hour, and you'd tell me to double my speed, I would go to 120 miles per hour, not 120 miles per 2 hours (which is equal to 60 miles per hour).
Regards,
Swan
edit on 26-12-2013 by swanne because: (no reason given)
I like what you've done, there, but I must point out a flaw:
When you square a ratio, you have to square the numerator and the denominator, and you also have to square the units. i.e.
(5 meters / second) squared becomes (25 meters squared / second squared)
(5 meters / 2 seconds) squared becomes (25 meters squared / 4 seconds squared)
Also note that 25 meters squared is a measurement of area (two dimensional space), not length (one dimensional).
swanne
The "c" component represents a very specific, fixed speed: light speed (299,792,498 meters per second). As you know, speed is, in fact, reducible to two components: distance divided by time.
In "c^2", only the distance is squared, not the time component. By this I mean that for instance, if "A" would represent "5 meters covered each 1 second", then "A^2" becomes "25 meters covered in 1 second", and not "25 meters covered in 5 seconds".
When you square a ratio, you have to square the numerator and the denominator, and you also have to square the units. i.e.
(5 meters / second) squared becomes (25 meters squared / second squared)
(5 meters / 2 seconds) squared becomes (25 meters squared / 4 seconds squared)
Also note that 25 meters squared is a measurement of area (two dimensional space), not length (one dimensional).
reply to post by swanne
Cool swanne! I always enjoy seeing what you come up with next. Something ive always wondered about and attempting giving thought to but never enough solid and precise and focused thought to fully comprehend the significance is; In E=Mc^2, what is the true significance of the speed of light squared? Out of all the values and numbers in the universe and in theory, why is that value so intimately linked with mass and energy, very intriguing ya?
Cool swanne! I always enjoy seeing what you come up with next. Something ive always wondered about and attempting giving thought to but never enough solid and precise and focused thought to fully comprehend the significance is; In E=Mc^2, what is the true significance of the speed of light squared? Out of all the values and numbers in the universe and in theory, why is that value so intimately linked with mass and energy, very intriguing ya?
reply to post by swanne
If we let x = 2m/2s = 1 m/s, then x² = 4m²/4s² = 1 m²/s². That does indeed "work" because 1² = 1.
If we set x = 4m/2s = 2 m/s, then x² = 16m²/4s² = 4 m²/s² = (2 m/s)².
Math always works. Never try to second-guess it.
TheRedneck
(I am using x instead of c because c is an experimentally proven constant for the speed of light in a vacuum. The intriguing part of your OP is that you showed how c being a constant also means the value of E/m is a constant, something I never really considered but which should have been obvious to me.)
If we let x = 2m/2s = 1 m/s, then x² = 4m²/4s² = 1 m²/s². That does indeed "work" because 1² = 1.
If we set x = 4m/2s = 2 m/s, then x² = 16m²/4s² = 4 m²/s² = (2 m/s)².
Math always works. Never try to second-guess it.
TheRedneck
(I am using x instead of c because c is an experimentally proven constant for the speed of light in a vacuum. The intriguing part of your OP is that you showed how c being a constant also means the value of E/m is a constant, something I never really considered but which should have been obvious to me.)
reply to post by darkbake
Seems Yorkshirelad concurs with you:
A fourth dimension is 90 degrees relative to all of the three existing dimensions.
That's right. Very well said.
Imaginary time. Interesting. I've been wondering about imaginary numbers representing another dimension in the normal x-y-z graphs.
Seems Yorkshirelad concurs with you:
there has to be an imaginary component (which really means a vector at 90 degrees or 270 degrees).
A fourth dimension is 90 degrees relative to all of the three existing dimensions.
When people speak of anti-matter, it's important to recognize that anti-matter isn't some sort of 'negative' matter. An anti-particle is just as real as any other particle. If you use Einstein's famous E=mc2 relation you find that an anti-particle has positive energy, since it has a mass which is identical to the mass of its partner 'particle.' The 'anti-' part of the name just signifies the fact that the quantum numbers that the particle has are opposite of those of the corresponding particle.
That's right. Very well said.
reply to post by Arbitrageur
Good point. In E=mc^2, energy-mass can vary but time (locked inside the "c" component) will always equal 1 second. As for my equation, the T value is dependent upon the energy-mass, and may not always equal 1 second.
Thanks for pointing this disparity to me, I'll have to check that up when I'll have more free time (pun not intended).
in the equation E=mc², d and t have a fixed ratio, and your equation doesn't represent that fixed ratio.
Good point. In E=mc^2, energy-mass can vary but time (locked inside the "c" component) will always equal 1 second. As for my equation, the T value is dependent upon the energy-mass, and may not always equal 1 second.
Thanks for pointing this disparity to me, I'll have to check that up when I'll have more free time (pun not intended).
reply to post by ImaFungi
It seems that the original equation is a bit more complex than that. We use E=mc^2, but this is just a contraction of a bigger equation where c is actually written as "c^4": upload.wikimedia.org...
As you see, in the original equation, "c" was not squared, but was actually at power 4: c^4. As some of these components would cancel out and/or were less important, we often reduce it to E=mc^2.
I don't know why c has to be squared (or put to the fourth power). I do know though that our universe has at least 4 dimensions...
It seems that the original equation is a bit more complex than that. We use E=mc^2, but this is just a contraction of a bigger equation where c is actually written as "c^4": upload.wikimedia.org...
As you see, in the original equation, "c" was not squared, but was actually at power 4: c^4. As some of these components would cancel out and/or were less important, we often reduce it to E=mc^2.
I don't know why c has to be squared (or put to the fourth power). I do know though that our universe has at least 4 dimensions...
edit on 27-12-2013 by swanne because: (no reason given)
reply to post by swanne
Ok C being ^2 or ^4 is interesting. But im asking why C at all; What is it about the value of the speed of light, relates to the relationship between mass and energy?
Ok C being ^2 or ^4 is interesting. But im asking why C at all; What is it about the value of the speed of light, relates to the relationship between mass and energy?
reply to post by VictorVonDoom
Right... and if 5m/2s equals 2.5m/1s, then its square is indeed 6.25m/1s, or again 25m/4s.
I used to reduce all denominators to 1, so I incorrectly assumed that squaring it was redundant. My bad!
Hm... in Einstein's equation, isn't c^2 (which was originally written as "c^4") actually a measurement of speed?
(5 meters / 2 seconds) squared becomes (25 meters squared / 4 seconds squared)
Right... and if 5m/2s equals 2.5m/1s, then its square is indeed 6.25m/1s, or again 25m/4s.
I used to reduce all denominators to 1, so I incorrectly assumed that squaring it was redundant. My bad!
Also note that 25 meters squared is a measurement of area (two dimensional space), not length (one dimensional).
Hm... in Einstein's equation, isn't c^2 (which was originally written as "c^4") actually a measurement of speed?
reply to post by TheRedneck
Okay, now this works for me as well. I would do,
If x = 4m/2s,
then x = 2m/1s.
thus x^2 = 4m/1s.
This even works for the square of 9m/3s. Since 9m/3s is equal to 3m/1s, then the logical result should be 9m/1s, or, again, 81m/9s.
Okay now it all makes sense. In my OP I had the instinct to always reduce the denominator to 1, and that's why I incorrectly assumed that squaring it was redundant. Thanks for making me realize my mistake!
If we set x = 4m/2s = 2 m/s, then x² = 16m²/4s² = 4 m²/s² = (2 m/s)².
Okay, now this works for me as well. I would do,
If x = 4m/2s,
then x = 2m/1s.
thus x^2 = 4m/1s.
This even works for the square of 9m/3s. Since 9m/3s is equal to 3m/1s, then the logical result should be 9m/1s, or, again, 81m/9s.
Okay now it all makes sense. In my OP I had the instinct to always reduce the denominator to 1, and that's why I incorrectly assumed that squaring it was redundant. Thanks for making me realize my mistake!
edit on 27-12-2013 by swanne because: (no reason given)
new topics
-
VP's Secret Service agent brawls with other agents at Andrews
Mainstream News: 40 minutes ago -
Sunak spinning the sickness figures
Other Current Events: 1 hours ago -
Nearly 70% Of Americans Want Talks To End War In Ukraine
Political Issues: 1 hours ago -
Late Night with the Devil - a really good unusual modern horror film.
Movies: 3 hours ago -
Cats Used as Live Bait to Train Ferocious Pitbulls in Illegal NYC Dogfighting
Social Issues and Civil Unrest: 4 hours ago -
The Good News According to Jesus - Episode 1
Religion, Faith, And Theology: 6 hours ago -
HORRIBLE !! Russian Soldier Drinking Own Urine To Survive In Battle
World War Three: 8 hours ago -
Bobiverse
Fantasy & Science Fiction: 11 hours ago -
Florida man's trip overseas ends in shock over $143,000 T-Mobile phone bill
Social Issues and Civil Unrest: 11 hours ago
top topics
-
Florida man's trip overseas ends in shock over $143,000 T-Mobile phone bill
Social Issues and Civil Unrest: 11 hours ago, 8 flags -
SETI chief says US has no evidence for alien technology. 'And we never have'
Aliens and UFOs: 15 hours ago, 7 flags -
Cats Used as Live Bait to Train Ferocious Pitbulls in Illegal NYC Dogfighting
Social Issues and Civil Unrest: 4 hours ago, 7 flags -
VP's Secret Service agent brawls with other agents at Andrews
Mainstream News: 40 minutes ago, 4 flags -
Former Labour minister Frank Field dies aged 81
People: 13 hours ago, 4 flags -
Bobiverse
Fantasy & Science Fiction: 11 hours ago, 3 flags -
HORRIBLE !! Russian Soldier Drinking Own Urine To Survive In Battle
World War Three: 8 hours ago, 2 flags -
Late Night with the Devil - a really good unusual modern horror film.
Movies: 3 hours ago, 2 flags -
Nearly 70% Of Americans Want Talks To End War In Ukraine
Political Issues: 1 hours ago, 2 flags -
Sunak spinning the sickness figures
Other Current Events: 1 hours ago, 1 flags
active topics
-
Mood Music Part VI
Music • 3100 • : TheDiscoKing -
VP's Secret Service agent brawls with other agents at Andrews
Mainstream News • 12 • : xuenchen -
Ditching physical money
History • 19 • : 20241105 -
Breaking Baltimore, ship brings down bridge, mass casualties
Other Current Events • 484 • : ThatSmellsStrange -
SETI chief says US has no evidence for alien technology. 'And we never have'
Aliens and UFOs • 39 • : SchrodingersRat -
Truth Social goes public, be careful not to lose your money
Mainstream News • 127 • : xuenchen -
15 Unhealthiest Sodas On The Market
Health & Wellness • 42 • : ThatSmellsStrange -
President BIDEN Vows to Make Americans Pay More Federal Taxes in 2025 - Political Suicide.
2024 Elections • 120 • : ImagoDei -
Nearly 70% Of Americans Want Talks To End War In Ukraine
Political Issues • 6 • : budzprime69 -
HORRIBLE !! Russian Soldier Drinking Own Urine To Survive In Battle
World War Three • 25 • : Freeborn
