Imaginary Numbers

Here are 3 short videos which sum up what imaginary numbers are and how much we don't understand them:

www.youtube.com...
www.youtube.com...
www.youtube.com...

Now I want to dig a bit deeper now and examine the range of operational rules which apply to imaginary numbers. We know the rules for multiplying imaginary numbers with real numbers and other imaginary numbers, and I have shown some algebra which demonstrates why it works. The general rules for multiplication are as follows:

4i x 2 = 8i
-4i x 2 = -8i
4i x -2 = -8i
-4i x -2 = 8i

4i x 2i = -8
-4i x 2i = 8
4i x -2i = 8
-4i x -2i = -8

Now to figure out how division works it should be a simple process of applying the same shifting rules observed with multiplication, but we invert the process by using a division operation instead.

4i / 2 = 2i
-4i / 2 = -2i
4i / -2 = -2i
-4i / -2 = 2i

4i / 2i = -2
-4i / 2i = 2
4i / -2i = 2
-4i / -2i = -2

Now what if we want to take it a step further and do what most mathematicians will tell you is impossible? How do we do addition and subtraction with imaginary numbers? Well the algebra we already use shows us that we can easily do 2i+1i and get 3i or we can do 2i-1i and get 1i.

But what about if we want a single solution to 4+4i? Well if you're paying attention, 4+4i is in the form of a complex number (a+bi) and we are taught that you can't simplify something like that. However I'm going to argue it is possible to add or subtract an imaginary number with a real number.

I will use some fairly simple algebra to prove my point and show that there are specific addition and subtraction rules which apply to imaginary numbers. I'm starting to feel very confident that the key to understanding imaginary numbers is to simply imagine them as normal numbers but which behave differently when operated on.

First we start with the square root of -16 which is found with the known rules:

√-16 = √16 x √-1 = 4 x 1i = 4i

So we can say that:

4i² = -16

And we can also say:

4i² + 4i² = -32

Now if we add 16 to each side of the equation we get:

16 + 4i² + 4i² = -16

We can substitute -16 with 4i² like so:

16 + 4i² + 4i² = 4i²

Now we can apply radicals to both sides and remove all the squared operations:

√16 + 4i + 4i = 4i

Then we can simplify the left side slightly:

4 + 8i = 4i

And finally we can subtract 4i from both sides:

4 + 4i = 0

Look at that, apparently 4+4i is equal to 0. But 4+4i is in the form of a complex number, it shouldn't be possible to simplify it into one value according to many people. However it appears I have just done exactly that here. And what does it tell us? It tells us that the addition operator works the opposite way to normal, much like multiplication using i.

We can use this one piece of information to essentially discern all the rules for how addition and subtraction works when dealing with imaginary numbers. For subtraction we can basically do the same thing we did before and invert the addition process, deriving the rules we need to complete the entire set of imaginary number operations.

When you think about the equation (4 + 4i = 0) or (2 + 4i = -2) or (6 + 4i = 2) or (-2 + 4i = -6) you realize that the rules for addition are very strange. The addition process actually behaves like a subtraction process. If you place the imaginary number before the real number you need to shift the sign of the result after doing the subtraction.

Consider the equation (-2 + 4i = -6). To solve this you simply do (-2 - 4 = -6). Just replace the addition symbol (+) with a minus symbol (-) and ignore the i. Here are the rules for addition:

4 + 2i = 2
-4 + 2i = -6
4 + -2i = 6
-4 + -2i = -2

4i + 2i = 6i
-4i + 2i = -2i
4i + -2i = 2i
-4i + -2i = -6i

So if we treat addition as subtraction, then we treat subtraction as addition:

4 - 2i = 6
-4 - 2i = -2
4 - -2i = 2
-4 - -2i = -6

4i - 2i = 2i
-4i - 2i = -6i
4i - -2i = 6i
-4i - -2i = -2i

Also note how the addition and subtraction rules are different from multiplication and division rules. If you multiply or divide an imaginary number with an imaginary number the result is always a real number. However the result is always an imaginary number if you multiply or divide an imaginary number with a real number.

The opposite trend occurs with addition and subtraction, meaning if you subtract or add two imaginary numbers the result is always imaginary and if you subtract or add a real number with an imaginary number the result is always real. With all these rules in place it should be possible to do mathematics with imaginary numbers directly.

One problem that may arise in the system I just detailed is the following.

What if we take 4 from both sides of this equation:

4 + 4i = 0

To get this equation:

0 + 4i = -4

That almost looks like it's saying 4i=-4, which we obviously know cannot be true. However I would point out that unlike operations with normal numbers, that addition symbol plays a key role in the equation. If it were 0+4 then you could drop the 0+ part, but I don't think that same rule applies when dealing with a mix of real and imaginary numbers because the whole idea of an imaginary number is that the operators behave differently.

So if we follow the rules for addition detailed above, the equation is really saying (0 - 4 = -4). Another point to notice about this is that if we replace the addition symbol with a minus symbol we get a different result.

0 - 4i = 4

We treat the subtraction operator as an addition operator in this case, which gives us a result of 4 and not -4.

reply to post by ChaoticOrder


So what stops us further simplifying:

4 + 4i = 0

4i = -4

i = -4/4

i = -1

It still maintains mathematical integrity as it expresses the imaginary as a real... I know the system breaks as we put the result back in the top

4i² = -16

4 x -1^2 = -16

16 = -16

But maybe it is not broken as this is what imaginary numbers do in reversing the sign operations?

reply to post by kwakakev

4i = -4

i = -4/4

i = -1

edit: ok I see the problem here too. i isn't equal to -1, i² is equal to -1. So yes, the problem occurs when you assume 4i=-4 as I mentioned in the post above yours.

4i² = -16

4 x -1^2 = -16

16 = -16

The problem with this is that it's not actually (4 x i²), it's (4i)². The difference is confusing I know. I should have made that clearer.

reply to post by ChaoticOrder

lol I think my brain just malfunctioned upon reading that.

It has been a good thread for it, lol.

I agree that i = -1 is not an accurate equality, but am considering it a real representation of the imaginary. With all the talk about dimensions, I view a dimension just as a variable. With large equations having many inputs, it can be viewed as multidimensional when mapping out all the inputs and their relationships. As information towards a specific aim is gained through calculations, information is also lost as the outputs are compressed into specific values and some of that is going on here.

I do not get how 4 + 4i = 0 is not equivalent to 4i = -4. I have heard how the practical use of imaginary numbers in a complex setting does not allow for this and the justification. It does suggest to me that the real relationship is then i(4 + 4j) = 0 or something similar if it keeps breaking here.

(4 x -1)^2 = -16 is right, good pickup.

In looking at e^-(i*Pi) = -1 for another approach as to what is going on and first ignoring the sign flipping, any real number taken to the power of 0 will result in 1. This does suggest that there is nothing special with e and pi in this equation as i is responsible for a couple of irrational numbers becoming rational. e and pi are clearly defined values with i the only unknown component and 0 the only real number to match in values.

So is it right to say x^-(i*y) = -1 and if not, what is so special about e, pi and i?

reply to post by ChaoticOrder


i represents the square root of -1 so i^2=-1
therefore 4 x i^2 is -4 is it not?

But we're getting into major semantics over a relatively simple but majorly useful mathematical tool IMHO.

Oops - ignore this as I just realised I stated the obvious that had already been stated (double redundancy)

reply to post by kwakakev

I agree that i = -1 is not an accurate equality, but am considering it a real representation of the imaginary.

But i² equals -1, not i. I can sort of see what you are trying to say but its just not valid algebraically. If you say i=-1 then you can say 4i is equal to -4, which it clearly isn't.

I do not get how 4 + 4i = 0 is not equivalent to 4i = -4.

I attempted to explain why several posts ago. The whole thing about imaginary numbers (or so I claim) is that they behave differently to normal numbers when operated on. So you can't simply drop the real part of the expression without first determining how it will effect the imaginary part. You need to think of it as if it were really 0+4i=-4.

The operators are the key to imaginary numbers. Keep in mind that 4i+0 is the same thing as 0+4i, they both equal -4, but they are not the same as just 4i. This is really not much stranger than the shifting process which occurs with i^n. So (4i + 0 = -4) becomes the following (remembering that we treat addition as subtraction):

4 - 0 = 4

Since the imaginary number comes first we flip the sign of the result to get -4.

reply to post by Pilgrum

4 x i^2 is -4 is it not?

Yes, (4 x i²) is equal to -4, but (4 x i)² is not.

Lets just say i was equal to 2 (it isn't).

4 x 2² = 16
(4 x 2)² = 64

When I see an expression like 4 + j4 I see a complex number IE it has a real and imaginary component so those two numbers cannot be simply added as they describe points on 2 axes displaced 90 degrees from each other. It describes a vector of length 5.66 at an angle of 45 degrees above the real (X) axis. To simply add the 2 numbers they need to both be of the same type (either real or imaginary).

A lot of previous posts would be very confusing to the uninitiated and I'm probably not making it much clearer here either.

reply to post by Pilgrum

When I see an expression like 4 + j4 I see a complex number IE it has a real and imaginary component so those two numbers cannot be simply added as they describe points on 2 axes displaced 90 degrees from each other.

Yes you are completely correct in your thinking here, that's the way it's taught and that's the way you should probably just continue to work with imaginary numbers. What I have presented here is something completely new, you wont learn it anywhere. Basically I'm trying to argue that you can in fact add or subtract an imaginary number with a real number (see the 2nd post from the top of this page).

reply to post by ChaoticOrder


Well yes you can mix them up because i has been assigned a value but does the result have any actual meaning?
IE real and imaginary numbers exist on their own unique planes so mixing them is like mixing apples and oranges so what you get is a mush that's neither one nor the other (tastes good though).

I am starting to take the view that imaginary numbers are like mathematical scaffolding, they help get to the next level, but not quite strong enough to build a lasting foundation.

So you can't simply drop the real part of the expression without first determining how it will effect the imaginary part. You need to think of it as if it were really 0+4i=-4.

This is what I mean by i(4 + 4j) = 0. In this case, i is the determining factor. What if i is a quadratic equation representing multiple points for a given value? Could this help account for the sign reversal?

If you are looking to do some magic with imaginary numbers then I am currently more inclined to see what is being missed in their application rather than applying them to new endeavours. Keep it real.

reply to post by Pilgrum

IE real and imaginary numbers exist on their own unique planes so mixing them is like mixing apples and oranges so what you get is a mush that's neither one nor the other (tastes good though).

We can multiply or divide imaginary numbers with real numbers so I see no adequately solid reason why addition and subtraction is out of the question. Your problem, like many others here, is that you have linked the concept of a complex number too tightly with the concept of an imaginary number in your mind. You don't need to learn about complex numbers to learn about imaginary numbers. Dealing with complex numbers is nice and useful because we can have a number which contains two objects which behave very differently. But I don't believe it's impossible to "mix" real and imaginary numbers, if we simply think of them as normal numbers which behave differently when operated on. When you visualize imaginary numbers in that way it's obvious that addition and subtraction with real numbers is possible.

reply to post by kwakakev

Could this help account for the sign reversal?

It's really quite obvious why that happens. A sign reversal is the only way that you can reach the square root of -1 or any other negative number. Think about it... 2 x 2 is 4 and -2 x -2 is 4. The only possible way we can have a number which when multiplied by its self equals a negative number, is if a multiplication operation on that number can produce inversed signs. When you ask what is the square root of -16 all you need to do is find the square root of 16 and than transform it to the imaginary form.

So if √16=4 then √-16=4i. You see, an imaginary 4 multiplied with an imaginary 4 has that special sign shifting behavior which gives us a result of -16. It's not that 4i is some weird mysterious quantity that we can't imagine, it's just a number like any other number, but it behaves in that special way when we operate on it. We know √1=1 and thus √-1=1i. Therefore it's obvious that 1i represents the imaginary version 1.

Now think about this and it makes perfect sense:

1 x 1 = 1
1 x 1 x 1 = 1
1 x 1 x 1 x 1 = 1
1 x 1 x 1 x 1 x 1 = 1

1i x 1i = -1
1i x 1i x 1i = -1i
1i x 1i x 1i x 1i = 1
1i x 1i x 1i x 1i x 1i = 1i

But I don't believe it's impossible to "mix" real and imaginary numbers, if we simply think of them as normal numbers which behave differently when operated on.

...but what you have not done is explain WHY? what is the purpose of this exercise. you've gotten some excellent feedback from micpsi and manfromeurope, but it appears that in both cases you were dismissive of their advice.

all you need to do is find the square root of positive 9 and than convert it to the imaginary representation of the same number, which would be 3i, and that is the correct answer to the square root of -9 if you solve it algebraically.

this is the only place in this thread where your claim of imaginary numbers being "different than" real numbers makes any sense. i admit, you had me stumped for quite a while (what the heck can he be talking about?!) you've posted some videos of mathematicians and physicists proclaiming the mystery of envisioning these beasts (i assure you, they have no difficulty imagining them, they are just being generous to the uninitiated.)

...but i can see now, from your quote above, that you are taking a very simple position after all...

...and in the process, destroying the entire purpose of relegating real and imaginary units in the first place...

lemme ask again: WHY?

Originally posted by ChaoticOrder
There is no number on the real or imaginary number line which when multiplied by its self equals an imaginary number.

in my previous post back on page 2 of this thread i gave a link to some infos about hypernumbers (wiki article here). i will reiterate to you that i think this info will be quite helpful to you in imagining what an imaginary number is. he has extended the concept just about as far as it can go, and has given many colorful descriptions of these fields of numbers which aid in envisioning the "shape" of the number system.

to address your above quote: in the hypernumbers, i think you will find there are multiple imaginary multiplication tables. and in some of these tables, you will find that multiplication of two imaginary units result in another imaginary number.

also in my previous post i posted an image of the solutions of polynomials in the range of 'i'. after reading this whole thread and understanding the type of arithmetic you are attempting on the imaginary unit, i truly think that image is the closest thing you can come to in understanding what the imaginary number "looks like". it is a beautiful example of the behavior of the isolated imaginary unit as it is approached as a solution. the positions in that image where the color density is brighter (or darker) will behave differently than what you have outlined in the operational scheme you have been proposing in this thread.




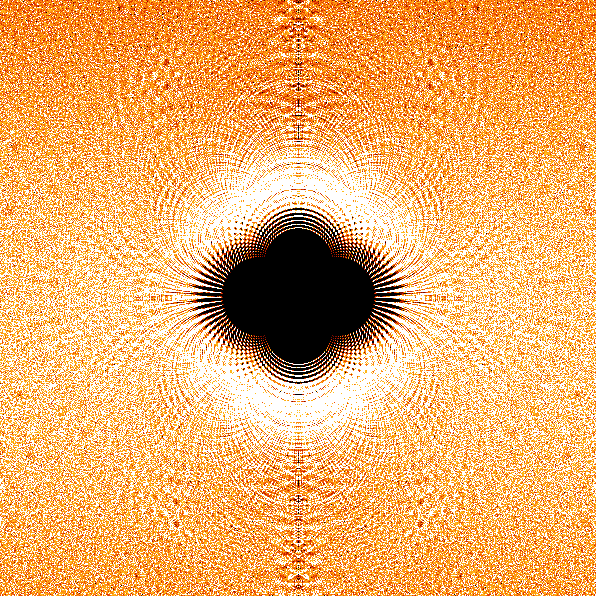
i agree that it is sometimes useful to talk yourself through these concepts....sometimes to the point of confuzing the hell out of yourself. and so long as you come out UN-confused in the end, i think you will be more-the-better.

so, the time has come for you to become unconfused.


good luck!

reply to post by tgidkp

...but what you have not done is explain WHY? what is the purpose of this exercise.

Why? Because having the ability to directly do arithmetic with imaginary numbers is a highly desirable tool and I'm certain if it works as I describe it, there would be many applications for it.

you've posted some videos of mathematicians and physicists proclaiming the mystery of envisioning these beasts (i assure you, they have no difficulty imagining them, they are just being generous to the uninitiated.)

Now you're just in denial my friend.

in my previous post back on page 2 of this thread i gave a link to some infos about hypernumbers (wiki article here). i will reiterate to you that i think this info will be quite helpful to you in imagining what an imaginary number is.

From the wiki article:

Musean hypernumbers are often perceived as an unfounded mathematical speculation

And that other link reads more like metaphysics rather than mathematics.

reply to post by ChaoticOrder

A sign reversal is the only way that you can reach the square root of -1 or any other negative number.

It is if our inputs are only limited to the 1st or 3rd quadrants of the Cartesian plane. This is what got me thinking about some deeper quadratic process. Instead of some liner relationship defining both side of the square as either both positive or both negative. We have a situation where one side of the square is negative and the other positive for some reason.

If the inputs have a half charge it could also account for √-1 and its subsequent stepping through imaginary and real values as the power rises.

reply to post by kwakakev

We have a situation where one side of the square is negative and the other positive for some reason.

Does that statement even make logical sense? The square of a number means a number multiplied by the exact same number. You cannot say "one side of the square is negative and the other is positive" because then it's not a squared operation. Unless I'm misunderstanding you...

reply to post by ChaoticOrder


so, rather than read the article, you read the opening paragraph, decided that the whole thing is bunk, and quit reading? yes, I see now how serious of an investigator you are.

a half page down from that, it reads...

The first two levels in hypernumber arithmetic correspond to real and imaginary number arithmetic. The basis after Musès is identical to j from the split-complex numbers, and is a non-real root of . Epsilon numbers are assigned the 3rd level in the hypernumbers program.

in other words, the hypernumber concept involves all of the accepted complex number systems (quaternions, split-quaternions, etc.) and extends them into levels which are so abstract that most mathematicians have been unable to understand.

so, rather than read and absorb information from someone who has a firm grasp on your proposal, you will prefer to assume that I am somehow misled? have fun spinning yer wheels.