Coincidence and the birthday paradox

and I can show you by using elementary mathematics, nothing beyond multiplication and division.

Simple mathematics???

Mate, the maths you used here, is way above my math skills. lol.

Sorry, I lost you half way through the thread.

vv

I have to say this has my brain frying. The mathematics is relatively simple to understand, and the implications could be interesting. This would imply that not only do 'coincidences' (I prefer the term synch) occur, but they occur often. Now would the viable sampling space for this be only a single persons experience? or would it be for the whole of the total number of people sampled?

Interesting post. Is there any way you can simplify it further for those of us that are mathematically challenged?

I'm mathematically challenged. What is the birthday paradox about?

I'm not mathematically challenged, but still didn't understand! Haha.
Very interesting concept though, please simplify further if possible?

[snipped at user's request]

My head hurts

And I thought I was good in math.....I am so lost right now its not even funny..

sounds interesting though

reply to post by Cryptonic

I don't quite know how to answer. For one thing, I hardly ever concern myself with coincidences/synchronicities which occur in day-to-day life; I have my hands full with grading, tutorials, papers, that sort of boring stuff

For another, it is often--rather, always--the case that we cherry-pick what is "relevant" and what is not. In fact, even if we read all the history books... the history books are all cherry-picked! If we could store a sufficiently large and well-distributed set of statistics, we could get a more conclusive answer.

Here is a page on the coincidences/synchronicities surrounding the number of "elevens" which show up around the 9/11 incident (plus a deliciously sarcastic retort). In this case I'd venture that we have on the order of 10^7 pieces of information.


Now, the explanation for those who are lost. It's good that people are curious about it. Maybe it will get people to do more math? I don't know.

Say you have some objects, represented by Xs. You have a group of people. Each person is allowed to pick one X. More than one person can pick the same X. What are the chances that more than one person picks the same X?

For the sake of simplicity, let's have 5 Xs and 2 people.

X X X X X

We can list out all the ways which 2 people can pick from 5 Xs by representing them as sequences of numbers: 11, 12, 13, 14, 15, 21, 22, 23, etc. For example, 42 means the first person picks the 4th X and the second person picks the 2nd X.

You can figure out how many ways there are in total by listing all the ways (there are 25 in total if you list them all out) or calculating. Since there are 5 choices for each person and 2 people, there are 5^2 = 25 ways.

This formula works for any N Xs and S people. For example, if N = 3 and S = 3 there are 3^3 = 27 ways. Although 27 is quite small, one would rather not list out all the ways for N = 365 and S = 23. That means it is a good idea to make a formula. And we have.

Now here's the tricky part. How many ways are there in which more than one person picks the same X? This time we have to dive straight in to the formula. The trick is to exclude the ways in which all people pick different Xs.

For the case of 5 Xs and 2 people, the first person has 5 choices, the second person has 4. So we have 5 * 4 = 20. It looks like this listed out: 12, 13, 14, 15, 21, 23, 24, 25, etc. We exclude these ways from the total, so we have 25 - 20 = 5.

For the case of 5 Xs and 3 people, the first person has 5 choices, the second has 4, the third has 3. So we have 5 * 4 * 3 = 60. There are 5^3 = 125 ways in total, so excluding them we have 125 - 60 = 65.

This kind of product, for instance 10 * 9 * 8 * 7, where we start with a number and multiply and decrease over and over, can be expressed using factorial notation: 3! = 3 * 2 * 1, 4! = 4 * 3 * 2 * 1, and so on. Therefore, 10! / 6! = 10 * 9 * 8 * 7.

Similarly, for the case of N Xs and S people, we exclude N! / (N - S)! ways.

To put it all together:
There are N! / (N - S)! ways to exclude
There are N^S ways in total
After excluding, we get N^S - N! / (N - S)!
Dividing by the total number of ways, we get (N^S - N! / (N - S)!) / N^S
Simplifying to 1 - N! / ((N - S)! * N^S)

Which is the collision function stated in the OP.

The birthday paradox is just a "surprising" result obtained from plugging in N = 365 and S = 23 into the collision function.

As an aside... how do people expect to wrap their heads around the serious stuff like astrophysics, classical thermo- and electrodynamics, and quantum mechanics while being stumped by probability/combinatorics?

Here is a plot of the BPN function for N up to 10^7.



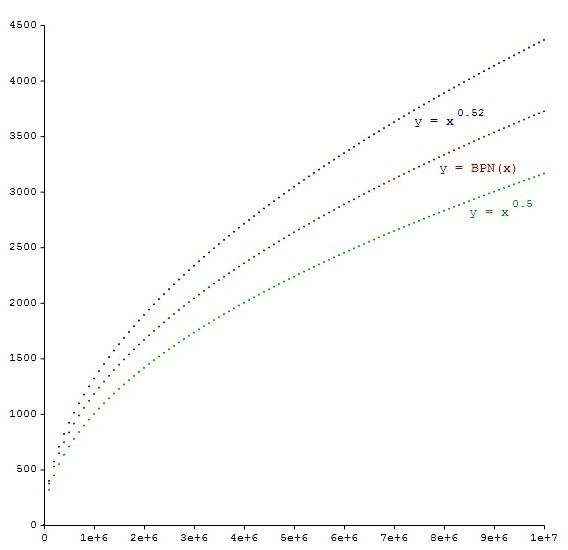
The functions y = x^0.5 and y = x^0.52 are also shown for comparison. All functions are colour-coded.

It seems from this image that the growth rate of BPN is between y = x^0.5 and y = x^0.52. Therefore according to this image the limit BPN(x) / x tends to zero. However, actually proving the bound for BPN will fly over most people's heads.

That is truly fascinating! Those of you who don't quite understand, just break the formula down piece by piece, when you understand the individual values you can understand the concept dont feel bad either, you are only proving the failure of school systems to teach problem solving and data processing skills XD

I alway thought that coincidence could be quantified mathematically but never spent much time thinking on the subject... This in a way proves that coincidence is simply a mechanism of reality as we perceive it! Awesome thread, just love it!

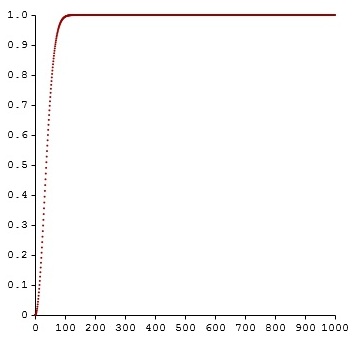
I can plot the probability of at least K collisions occurring, not just one collision; that would be more meaningful because synchronicities often happen in bunches. For now, I have plotted the probability of the simple case, encountering at least one collision.

Here is a plot of y = C(50, x).


Here is a plot of y = C(100, x).


Here is a plot of y = C(1000, x).

Its some nice maths you have there, but you haven't convinced me that Synchronicity doesn't exist.

Mainly, you are starting with an assumption that there is no connections between events, or that all events are discrete. You also assume there is no meaning in those connections. These assumptions may not be true - for example in your birthday example, there are going to be effects of the seasons, politics, climate, economy etc on when people are born. So while you can give the probability of two people sharing the same birthday, you've made no comment on how or why they do. This is the deeper nature of synchronicity that pure maths cannot explain.

e.g. Jack and Jill take part in one of your example experiments. It turns out that they share a birthday. Not really that special according to your theory. But what if they share a birthday because both their sets of parents went to watch the same romantic movie on the night of conception? What's the chances that both their parents went to that movie, then concieved around the same time, then the babies were born at around the same time, then they both grew up, came to the same place and both volunteered for your experiment? I am no mathematician, but I expect the odds are astronomical.

That's just a hypothetical example, but my point is its not as simple as you are trying to make it. It doesn't mean its impossible for it to be purely chance, but IMO when you look at the deeper connections behind "coincidences" and especially what they mean to individuals, your theory goes out the window.

Probability is an abstract concept not strictly related to reality. If you are about to flip a coin, there is theoretically a 50/50 chance of heads or tails. But that doesn't actually tell you anything about what will happen, how or why. After you flip the coin the probability of heads is either 1 or 0, because it was either heads or tails. If you flip a million coins you'd expect 500,000 heads and the same number of tails, but in any individual experiment that's never the case. Only as the number of flips approaches infinity do the actual results approach 50/50 - and that is impossible for us here in 3D space with limited time on our hands. So basically, its a model or approximation and can only be applied to large sample sizes.

When talking about a set of meaningfully related events, replete with personal significance, you can't apply probability.

This is simply an algorithm that denies infinity and assumes there are a perfect set of numbers. The only real number is the number 1 (infinite).

So actually , what you just explained was an infinity , or a vicious cycle if i remember correctly which defines either a very controlled or (created universe) or a very random universe that has existed for eternity and constantly recycles itself in an eternal (vicious cycle). This also suggests reality as we know it has no creation or destruction point. It simply regresses and explodes yet again for ever and ever and ever , then of course God comes into the picture.

So coincidences are only true in the fact that the function shown is false resulting in the function as unknowable - suggesting 100% complete randomness or design instead of mere coincidence.

However , current science says something cannot be created out nothing and you must have an action for a reaction.

So complete eternal randomness would be impossible as something cannot simply appear without an action in turn suggesting an Infinite could not exist without an infinite.

000000000000000000000000000000000000000 (repeating forever - void) (spark) 111111111111111111111111111 building blocks appear (creation or the big boom)

My professor was a Deist.

----------------------

However , it has been 3 semesters since I took Theoretical Physics , so I am a little rusty. It was the most interesting and hardest class i have ever taken. It explains the very real possibility of creation , but also explains the possibility that the Universe is a never-ending Cycle of proven immortality. Meaning the Universe will NEVER end as energy cannot be diminished , and if you have energy that does not diminish then you will also have the buildings blocks necessary for another big bang. However , the problem with that is , is it impossible for the Infinite (reality as we know it) to exist without an Infinite to make the infinite cycle ..


However , you are using logical fallacy to explain the probability of a coincidence to occur as well as a howler error , you are negating physics. A core component of the expansion of mathematics and the world around us.

Almost ALL coincidences in mathematics are actually casual functions and not coincidences at all. The only real coincidences that can be taken seriously as far as i know of are the platonic solids i believe , however , in physics , this further correlates to an intelligent design and are actually related to geometry which is very very interesting.

The platonics just so happen to be the sustaining life essence of all of existence. A Triangle seems to be the absolute perfect geometric shape , and represents all life as we know it.

The platonics ( forms of triangles basically) suggest that there is another infinite we cannot see or comprehend. A 'higher' dimension above this one , one that is the building block for this dimension.

What is funny ... our ancestors knew all of this before we accepted it .... weird. How the hell did they figure this out without having fancy particle colliders and fancy telescopes ?

-------------------------------------------------------------------

I am not trying to discuss religion and offend any one. However , in Theoretical Physics the main thing discussed is infinity. So you discuss creation (intelligent design) and an eternal universe a lot. However , things are an organized chaos , how does a random action create organization out of chaos in an eternity? It doesn't ... then of course you have quantum physics appearing and quantum physics is the second version of the class (introduction / discussion of quantum physics any way).

Exactly the kind of thing I was looking for. Thanks.

reply to post by Cecilofs

I am aware of what probability theory is and what it isn't. It isn't supposed to be perfect. It is a model. What does "the probability of an event" mean? It is a ratio between the size of a set and the size of a subset (hence its restriction to the range [0, 1]). Example: we model the outcomes of a fair 6-sided die using the set [1, 2, 3, 4, 5, 6]. We model the desired outcomes using a subset. Let's say we want a 4. Then we say [4]. The size of [4] is 1 and the size of [1, 2, 3, 4, 5, 6] is 6. We find that the probability of getting a 4 is 1/6.

Indeed, theory can be detached from real life. Probability theory is purely theoretical and thus only applicable before taking any samples. What actually happens doesn't matter; I could roll the die a million times and get a million 4s. But the probability of getting a 4 is still 1/6, because we have already decided on using [1, 2, 3, 4, 5, 6] and [4].

It seems to be a backwards way of thinking, so why do we use it? It is often easier--and thus more practical--than analyzing lots of samples.

As for your hypothetical:

What's the chances that both their parents went to that movie, then concieved around the same time, then the babies were born at around the same time, then they both grew up, came to the same place and both volunteered for your experiment? I am no mathematician, but I expect the odds are astronomical.

The space of possibilities is enormous. Anything could have happened to disrupt this chain of events: one of the parents has a car accident on the way to the hospital, one of the babies is born with a heart defect, one of the kids is sent to work in a salt mine. Yet, you can still model this space using a set, with each element representing a sequence of events instead of a single event. Even with astronomical odds against your hypothetical being chosen, it can still be chosen.

Here is an analogy. Suppose you shuffle a standard deck of 52 cards using a machine with such power that each permutation is equally likely. You shuffle using the machine. Out come the cards, sorted by rank and suit. Would that surprise you? But it would have been equally likely to see some meaningless jumble of cards. The point is that we determine what is meaningful. Maybe the order Ace of Clubs, Seven of Diamonds, Jack of Diamonds, etc. is meaningful to me.

As for Synchronicity: it is a matter of belief, much like belief in God. It is a concept derived from a somewhat liberal interpretation of quantum entanglement. For the interested, here is an article from Ars Technica about the misuse of QE. A passage from the article states:

Entanglement is delicate, rare, and short-lived.

It follows that "macro-entanglement" is nigh-improbable, amounting to solving an astronomical number of simultaneous wave equations.

I do not believe in Synchronicity; on the other hand, probability theory has already been applied to great effect. And with this statement you have shown me that Synchronicity is indeed a matter of belief:

you haven't convinced me that Synchronicity doesn't exist

That was never my intention in the first place.

I have already chosen to interpret the universe one way, and someone else may have chosen to interpret it a different way.

Be aware that I have also chosen not to involve myself in any mudslinging, as tempting as it may be.

Originally posted by TadeuszIndeed, theory can be detached from real life. Probability theory is purely theoretical and thus only applicable before taking any samples. What actually happens doesn't matter

I get what you are saying and I agree with this statement. IMO this is why you can't compare probabilities to synchronicity. Probability is a model for reality, but it is not reality. Likewise, it assumes that everything is random and that there is equal chance any of the outcomes could occur (in the case of a coin flip). The point I am trying to make is that's not necessarily the case - the coin was never going to be tails so the probability of heads was 1 all along, despite the model which says it should be 50/50.

As for your hypothetical: Even with astronomical odds against your hypothetical being chosen, it can still be chosen. Suppose you shuffle a standard deck of 52 cards using a machine with such power that each permutation is equally likely. You shuffle using the machine. Out come the cards, sorted by rank and suit. Would that surprise you? But it would have been equally likely to see some meaningless jumble of cards. The point is that we determine what is meaningful. Maybe the order Ace of Clubs, Seven of Diamonds, Jack of Diamonds, etc. is meaningful to me.

Yes, absolutely. While the perfect ordering is exactly as likely as any random ordering, it is significant to us. I agree we create our own meaning, I just don't think that means it isn't real

you haven't convinced me that Synchronicity doesn't exist....
That was never my intention in the first place.

Ok I may have misunderstood your posts. My understanding is that you were trying to show that even things which seem impossible are actually not that unlikely and therefore, we shouldn't be surprised when "random" events seem meaningful. i.e. That you don't think synchronicity is real, but rather that people arbitrarily assign meaning to events that SEEM impossible, but in terms of cold hard maths, they aren't.

It is a belief thing. You start with the assumption that everything is random, I start with the assumption that it isn't.

I have already chosen to interpret the universe one way, and someone else may have chosen to interpret it a different way.

Indeed. I always found the why more interesting than the how, but to each their own

reply to post by Cecilofs

It is a belief thing. You start with the assumption that everything is random, I start with the assumption that it isn't.

It's quite a popular thing on which people disagree. A related question is: do we have free will? These are questions with no answers. All the same, I would like to hear your opinion: what does it really mean when some things are not random? Does it mean that there is a higher power with some measure of control over the universe?

My opinion: hard determinism with probability. Every state has a well-defined set of next states to "choose" from, but we don't know which. Science is essentially materialistic and cynical; it seeks to prove this assumption wrong by building more and more intricate theoretical models of the universe. If we do achieve this, then we would pretty much have hit the jackpot--discovered the higher power behind the universe. Even if we never get there, then we would have at least advanced as a species.

While a scientist would love to see synchronicity in action, he would smother it with more theory and ask for more evidence

Originally posted by TadeuszIt's quite a popular thing on which people disagree. A related question is: do we have free will? These are questions with no answers. All the same, I would like to hear your opinion: what does it really mean when some things are not random? Does it mean that there is a higher power with some measure of control over the universe?

Yes I do think there is some sort of higher power or consciousness. Its exact nature I don't know, but I am trying to find out.

I believe in free will in that we chose to come here and experience this life. That our will and the will of "God" or whatever higher power is out there is the same and the goal is to align your will with the will of the universe.

Overall though, I believe that we create our reality (and co-create shared reality) and so some things that happen have a meaning internally for each individual, like a sign from ourselves to ourselves. Or if not meaning, then a purpose in that it carries us from one moment or place to the next so that we can have more experiences and learn more.

I admit though that the concept of a completely meaningless, random world depresses me, so its possible I just don't want to accept it. After all, if that is the case, then why do anything at all? Why not murder, steal, or just kill yourself?

reply to post by Cecilofs


You are doing what everyone does, that which makes the birthday scenario seem counterintuitive. This is the question you asked.

What's the chances that both their parents went to that movie, then concieved around the same time, then the babies were born at around the same time, then they both grew up, came to the same place and both volunteered for your experiment? I am no mathematician, but I expect the odds are astronomical.

This would be akin to asking what are the odds someone in the group of 23 shares YOUR birthday.

This is what you should have asked.

What's the chances that two sets of parents went to the same movie, then concieved around the same time, then the babies were born at around the same time, then they both grew up, came to the same place and both volunteered for the same experiment?

The difference being that you are falsely creating a coincidence by limiting the starting point to only two sets of parents. In reality you need to start with ALL parents who saw that movie.

Couples tend to see romantic movies.
Having sex after is not uncommon.
Conceiving on the same night will mean the babies will be born at the same time.
The parents were from the same area so the children will grow up in that area.
You may have 20 children born as the result of that steamy movie, you just need any 2 of them to end up at the experment to create the illusion of coincidence.

What you did was create coincidence, when in reality there is mathematical probabilities at work on an exponential level. Just because only 2 children showed up for the experiment does not mean they were the only 2 born. Some events have very low odds, but in a world with billions of people they will happen.