Why Pi = 3.141 .. instead of 3.144?

Originally posted by IblisLucifer

Pi (3.14159265...) can only be rational if you make 2 circles one inside the other put 2 on both sides of the inside one .[....] 9.1428571428571428571428571428571... much more rational

But the value you just used is based only on "successive approximation" of a curve into lines which fall short.
In the rational sense of yours you could use the "rational approximation" of 22/7. This has nothing to do with the sqrt(16/phi) or 4/sqrt(phi).

As I stated before on another post, "I am not saying that algebrally the use of "pi" is wrong, but that the arithmetic value is wrong as it is based on successive approximation of a curve into lines which fall short. What I have provided is closed form formula for calculating the arithmetic value (A closed-form-derivation of Pi by breaking a square into 16 parts that Phi can be expressed in terms of a circle's area and circumference). "

Blah...Blah...Blah...that is what I am hearing (reading)!

It is simple....3.141....lets see:

There are various other ways of finding the Lengths or Areas of particular Curve Lines, or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to the Circumference as 1 to ... 3.14159, etc. = π

Ahhh...Pi....

reply to post by jerryznv


Bah, your statement is begging the question (but it is good example of circular logic! )
Booze is a drink of the wise ones, so wise is the one who drinks booze..

4 cos(pi / 4) = 2.82842712
sqrt(10) = 3.16227766

Originally posted by JackTheTripper
reply to post by jerryznv

 

Bah, your statement is begging the question (but it is good example of circular logic!

)
Booze is a drink of the wise ones, so wise is the one who drinks booze..

edit on 10-12-2011 by JackThBeTripper because: (no reason given)

Bah...and yours is left empty...what is the equation?

There is no awner to an unsolvable....not today anywany!

Eh, what are you talking about? Be more clear please. It seems you are justifying your claims by using an inaccurate approximation of pi.

Originally posted by 547000

Eh, what are you talking about? Be more clear please. It seems you are justifying your claims by using an inaccurate approximation of pi.

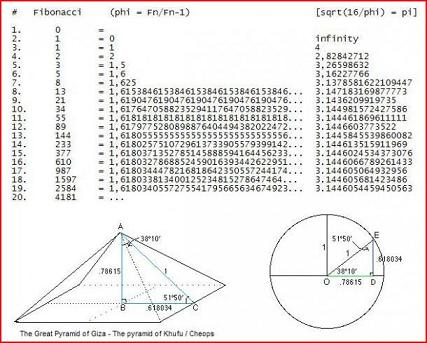
WHAT? I am instead claiming that the current standard of pi is based by inacurate approximation of pi and I am uttering a closed form formula for pi, which can be proofed (using mathematics) to be correct and which gives the pi value 3.1446011... Please do download the pdf from the link on my signature below. Read it and and tell me why it is not correct.

I can't understand it. Be more precise. Give definitions so the argument can be followed.

Stonehenge contains pi ~ 3.1446... as well!

Dude... You can measure it with a stick and a string and it will still be 3.14159...

If the radius is 1, a half circle is pi. All numbers are relative to the distance between 0 and 1, including the length of a curve. It's pretty simple. I've measured it myself.

You can't just throw fibonacci and phi at something and magically transform it.

The best connection I've found between phi with pi is this: 1/phi*2 = 0.309. When you're sine value is 0.309, the radian value is 0.314 (pi/10).

Originally posted by JackTheTripper

Originally posted by 547000

Eh, what are you talking about? Be more clear please. It seems you are justifying your claims by using an inaccurate approximation of pi.

WHAT? I am instead claiming that the current standard of pi is based by inacurate approximation of pi and I am uttering a closed form formula for pi, which can be proofed (using mathematics) to be correct and which gives the pi value 3.1446011... Please do download the pdf from the link on my signature below. Read it and and tell me why it is not correct.

There are many "proofs" which once they were completed have proven to be paradoxical.

See Euclid for starters....

With that said, there is much more to Mr. Fibonacci than meets the eye. Many real mathematicians know this. It's just that they can't quite put their finger on exactly what "it" is.

Yet...

Supercomputers crunch away and hope springs eternal....

Great thread OP. S + F for you!

Originally posted by Riffrafter

There are many "proofs" which once they were completed have proven to be paradoxical.

See Euclid for starters....

With that said, there is much more to Mr. Fibonacci than meets the eye. Many real mathematicians know this. It's just that they can't quite put their finger on exactly what "it" is.

Yet...

Supercomputers crunch away and hope springs eternal....

Referring to the 47th or to the Euclidean Algorithm?
Yet, finally words I can comprehend... Farewell, traveller!

reply to post by JackTheTripper







I’m not exactly up to scratch on the mathematics on all this, but I know it’s quite complex. Check out the video above at 0.39:00, there’s some interesting geometry around squaring the circle, found within crop circles…it’s pretty amazing stuff.


- JC

Originally posted by circlemaker
Dude... You can measure it with a stick and a string and it will still be 3.14159...

If the radius is 1, a half circle is pi. All numbers are relative to the distance between 0 and 1, including the length of a curve. It's pretty simple. I've measured it myself.

You can't just throw fibonacci and phi at something and magically transform it.

The best connection I've found between phi with pi is this: 1/phi*2 = 0.309. When you're sine value is 0.309, the radian value is 0.314 (pi/10).

Yes, well - I think I have come to conclusion with this. As there is no straight line in nature, the lenght of the circles diameter - when (maginarily) drawn will vary and thus approximate using the golden rule to the perfect straight line. When the (imaginary) line is measured by following exactly the line, it is slightly longer than the exact approximation of pi value (3.141...). In a sense the value 3.144 does meet the description of "circle's circumference to its diameter".

From The infernal prime spiral -page
At the beginning (Graph 1), we can only see 2 rotating arms in the spiral. But gradually (Graph 2 and 3), we can see 2 big arms in which we have exactly 10 little arms.Why 10 ? I never used this number neither in the function nor in the program. Now, if we take x in degrees, we obtain a simple Archimede spiral less and less dense (due to the prime numbers rarefaction). So, would it be an hidden property of pi ?

- Isaac Keslassy (11 Apr 1999), who has found that it wasn't a property of pi but a property of a range including pi (3.141 to 3.144) : curious, no ?

[...]

- Erick Wong (03 Oct 1999), for his excellent explanations of all the phenomenas. Here are extracts from the mail:

The prime spiral on your web page is easily explained in terms of rational approximations to 2*Pi (this is why numbers close to Pi also work, since they have the same approximants).
The best rational approximations for 2*Pi, given by the continued fraction 6+1/(3+1/(1+1/(1+1/(7+1/(2+...))))) are 6/1, 19/3, 25/4, 44/7, 333/53, 710/113, ...
Now, imagine plotting the numbers (6n+1) in radians. We get the spiral instead of a straight line because 6 is not exactly 2*Pi.
The spirals are counterclockwise because 6 < 2*Pi radians.
I think that 19/3 and 25/4 are not close enough to 2*Pi to be recognized, and 44/7 is much better. Well, Phi(44)=20 and that's why there are 20 arms (the two large "gaps" correspond to the spirals 44n+[10,11,12] and 44n+[32,33,34], which are never prime. Now the spirals are clockwise because 44>2*Pi*7.
As we zoom out further, I expect to find spirals corresponding to the very good approximation 710/113. and ther should be exactly Phi(710)=280 arms.

So please forgive my clearly insane or ridiculous babblings.
A postulate arises: As phi is constantly found in the nature, it may be that the closest approximation of perfect circle the nature can produce could be expressed using the formula 4/sqrt(phi).

reply to post by JackTheTripper


Pi is not just measurable by length but by area too. Measured it by both upper and lower bound it converges to 3.14159... Surely you agree that a figure that circumscribes a circle has a greater area and yet as the number of sides increases without bound the area does not converge to 3.144... I gave you a book to check out in the other thread. And I don't believe you understand that if the infinite series and algebraic relations are right, there is no reason that pi is calculated wrong.

it's quiet soothing when sung

I have a circle that is 100cm in diameter,
please tell me what the circumference is?

reply to post by JackTheTripper


The Pi that I was taught was 3.14159etc. Personally I would trust my Japanese academic math teacher over your (presumably) American math teacher any day of the week. And technically, both mainstream perspectives are wrong as it properly rounds up to 3.142.

I work in construction engineering and 3.141592 is as far as I ever take it and that is really technical overkill for solving real life mathematical/dimension problems. Why do I use the 3.141592 value...errr...because it is accurate and the stuff we build using this formula actually fits and I never have problems with it...that pretty much trounces anything else...practicality baby....this is what I do....

reply to post by Damrod


You are correct, but I'd still say the 4/sqrt(phi) is the best approach in nature while approximating to pi..
Take this mathematically drawn hamp leaf as an example.