It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
share:
cheap warning device...keep an eye on a fixed compass with north marked... because if the needle does not point in that same place any more overnight
something is up look up Edgar Cayce predictions you can even check out virtual flood maps online to see if you would end up under water...
reply to post by Lynda101
According to science homo sapiens only came 200.000 - 500.000 years ago.
But that's not the point i guess.
Many other species survived this event so i don't believe a pole shift would all we know and bring the end of the world.
But it's a good question if you think on the type of shift that could happen.
According to science homo sapiens only came 200.000 - 500.000 years ago.
But that's not the point i guess.
Many other species survived this event so i don't believe a pole shift would all we know and bring the end of the world.
But it's a good question if you think on the type of shift that could happen.
reply to post by intergalactic fire
You're right, I wrote homo sapiens, but I should have mentioned the lineage tracing back to australopithecus probably our first ancestor. I'm having one of those days when my body is working but my brain never got up this morning.
You're right, I wrote homo sapiens, but I should have mentioned the lineage tracing back to australopithecus probably our first ancestor. I'm having one of those days when my body is working but my brain never got up this morning.
Originally posted by intergalactic fire
Another question i wanted to ask,
If the magnetic poles change, is it possible the earth's rotation direction change also?
Anyone knows the theory why the earth spins counterclockwise?
No
the earth's rotation is whats still left from the momentum it got when all the dust and debris which formed the planet clumped together.
eventually the rotation speed was significantly modified when a (so the theory states) ' a mars sized object slammed into the earth, creating its moon'
the rotation-speed is slightly modified if the magma changes its way floating deep down our feet, but basically earth mass and the momentum picked up on creation is so immense that no INTERNAL process would be able to change its rotational direction completly
we may get slight variations in the range of milliseconds
changing the direction completly would require a similar sized mass to slam into the planet, which would result in a complete destruction of the planet as we know it.
the question why the earth spins this way around and not the other, is difficult to explain.
Its believed that the planet formed itself out of a debris disk around the sun which should have rotated the same way around the sun like the sun itself .. possibly being dragged by the sun itself in this direction.
Now we may had slight rotation variances at the location where the first fat pebble which later became earth formed, where the passing dust at the side facing the sun dragged on it at a different speed as the other side, and soon we got a slight rotating pebble.
Then a whole lot of more dust was assimilated in millions and millions of years, and ..similar to an ice-skater pulling its arm to the body...this mass aquisition speeds up the pebble to the rotation it still has today.
And since we have no sort of drag anymore today the earth will spin forever this way.
reply to post by intergalactic fire
I will let someone who actually believes in the crustal displacement theory stand in for that discussion
As far as the magnetic pole shift goes, as you showed, there is plenty of evidence for this. How it changes? I have my ideas on that. The electric universe theory has alot of interesting, and potentially valid ideas in it. I believe that we overlook the one major player in the solar system who very easily could be affecting our magnetic field directly.
milwaukee.indymedia.org/images/2009/06/211121.jpg
Our own sun has to have an electrical/magnetic impact on this planet. Now how it affects the pole shift I cannot say, as electricity and magnetism is one of my weak points, but if the Earths electrical/magnetic field is generated from dynamo effect, then the Sun's field would interact to some degree with ours. Maybe a perfect storm scenario is what it takes for the pole shift to occur ( Huge CME directed at Earth at the same time the Sun's pole flips? ).
All speculation on my part admittedly, and I have no evidence to back it up, but I firmly believe that everything in the solar system interacts not only gravitically, but magnetically and electrically too.
Danno
I will let someone who actually believes in the crustal displacement theory stand in for that discussion
As far as the magnetic pole shift goes, as you showed, there is plenty of evidence for this. How it changes? I have my ideas on that. The electric universe theory has alot of interesting, and potentially valid ideas in it. I believe that we overlook the one major player in the solar system who very easily could be affecting our magnetic field directly.
milwaukee.indymedia.org/images/2009/06/211121.jpg
Our own sun has to have an electrical/magnetic impact on this planet. Now how it affects the pole shift I cannot say, as electricity and magnetism is one of my weak points, but if the Earths electrical/magnetic field is generated from dynamo effect, then the Sun's field would interact to some degree with ours. Maybe a perfect storm scenario is what it takes for the pole shift to occur ( Huge CME directed at Earth at the same time the Sun's pole flips? ).
All speculation on my part admittedly, and I have no evidence to back it up, but I firmly believe that everything in the solar system interacts not only gravitically, but magnetically and electrically too.
Danno
reply to post by intergalactic fire
I am not sure how pole reversal could affect the rotation of the planet. An actual change of the direction of the rotation of the mantle and core would be super destructive to the crust. Once again, the Pacific and N American plates sheer size argue against that kind of major change. If major mantle/crustal disruptions have taken place in the past, those plates would be much more fragmented than they are.
I think the only thing that could potentially affect the actual rotation of the planet to the degree of actually reversing it would have to be an impact of something as large or larger than the earth. Think 2nd law of thermodynamics.....
EDIT: TMJ got to the rotation bit before I did
Danno
I am not sure how pole reversal could affect the rotation of the planet. An actual change of the direction of the rotation of the mantle and core would be super destructive to the crust. Once again, the Pacific and N American plates sheer size argue against that kind of major change. If major mantle/crustal disruptions have taken place in the past, those plates would be much more fragmented than they are.
I think the only thing that could potentially affect the actual rotation of the planet to the degree of actually reversing it would have to be an impact of something as large or larger than the earth. Think 2nd law of thermodynamics.....
EDIT: TMJ got to the rotation bit before I did
Danno
edit on 10/7/2011 by MoparDanno because: (no reason given)
reply to post by TMJ1972
I agree with everything you posted, but to take this a bit OT and play devils advocate......
What about Venus? Wouldn't Venus's retrograde rotation poke a hole in that theory? Or is it theorized that Venus was whacked with a very large mass at somepoint in its formation? It would have had to been pretty early on in the planets formation, as we have found no evidence of that size of a "dent" in Venus that I know of
Danno
I agree with everything you posted, but to take this a bit OT and play devils advocate......
What about Venus? Wouldn't Venus's retrograde rotation poke a hole in that theory? Or is it theorized that Venus was whacked with a very large mass at somepoint in its formation? It would have had to been pretty early on in the planets formation, as we have found no evidence of that size of a "dent" in Venus that I know of
Danno
Originally posted by Phage
While the magnetosphere does protect the atmosphere from the solar wind, it would take millions of years (in the event of a total collapse) for the atmosphere to be stripped away. Even with no magnetic field we would not be toasted but over a long time we may not have enough air to breathe.
edit on 10/7/2011 by Phage because: (no reason given)
And how do we know this?
Originally posted by MoparDanno
All speculation on my part admittedly, and I have no evidence to back it up, but I firmly believe that everything in the solar system interacts not only gravitically, but magnetically and electrically too.
True, but...
one have to be aware that those influences are just very very tiny over time.
The only two important things keeping the earth stable in its motion are
1. the rotation of the Earth-Moon system around the sun, since the suns mass gravitationally totally dominates the solar system and combines like 99.9% of the mass of the entire solar system
2. the gravitanional influence of the moon being exact THIS size and in THIS distance helping the earth to keep its axis stable. (see uranus for the results not having such a comparable companion)
From my point of view a whole lot of people overestimate influences from other sources too much, or can simply not imagine how hughe the solar system is, with the result that we have endless debates about Elinen here for example.
Nothing much can influence the planet here, otherwise history had like 4.5 billion years of time to mess things here totally up. which obviously did not happen.
reply to post by DieBravely
Your question is a bit ambiguous. How do we know what?
That the atmosphere protects us? Because electromagnetic radiation is unaffected by the magnetosphere. Because the levels of radiation outside of the atmosphere are much greater than those on the surface, even at the poles where particle radiation is directed toward the Earth's surface. As pointed out, the particles can be seen giving up their energy in auroral displays before they reach the surface.
That with no magnetosphere the atmosphere would be stripped away over time? Because that's what happened to the atmosphere of Mars.
science.nasa.gov...
And how do we know this?
Your question is a bit ambiguous. How do we know what?
That the atmosphere protects us? Because electromagnetic radiation is unaffected by the magnetosphere. Because the levels of radiation outside of the atmosphere are much greater than those on the surface, even at the poles where particle radiation is directed toward the Earth's surface. As pointed out, the particles can be seen giving up their energy in auroral displays before they reach the surface.
That with no magnetosphere the atmosphere would be stripped away over time? Because that's what happened to the atmosphere of Mars.
science.nasa.gov...
edit on 10/7/2011 by Phage because: (no reason given)
reply to post by alfa1
do you have any proof whatsoever for or against what happens when the earth crosses the galactic plane? didnt think so. and for a second i thought we had millions of years of data for you to back up your claim, but guess what? that is impossible.
do you have any proof whatsoever for or against what happens when the earth crosses the galactic plane? didnt think so. and for a second i thought we had millions of years of data for you to back up your claim, but guess what? that is impossible.
One problem to also consider is how the sun (consisting of the greatest majority of the mass in the solar system) contains a much smaller
percentage of the total angular momentum of the entire solar
system.
How has this energy been transferred to the planets?
This put me in mind of a post here:
Are things the way we've learned or is somehting else possible?
A possible weak link in the condensation theory is sometimes known as the angular momentum problem. Although our Sun contains about 1000 times more mass than all the planets combined, it possesses a mere 0.3 percent of the total angular momentum of the solar system. Jupiter, for example, has a lot more angular momentum than does our Sun—in fact, about 60 percent of the solar system's angular momentum. All told, the four jovian planets account for well over 99 percent of the total angular momentum of the solar system. By comparison, the lighter (and closer) terrestrial planets have negligible angular momentum.
How has this energy been transferred to the planets?
Originally posted by TMJ1972
snip
Then a whole lot of more dust was assimilated in millions and millions of years, and ..similar to an ice-skater pulling its arm to the body...this mass aquisition speeds up the pebble to the rotation it still has today.
And since we have no sort of drag anymore today the earth will spin forever this way.
This put me in mind of a post here:
Originally posted by JustMike
reply to post by Doodle19815
snip
Oh, just one thing I wanted to mention as it came to me while reading Jaded's post about the currently-unaccepted concept of an expanding Earth versus the currently-accepted theory of plate tectonics. I feel that seeing as plate tectonics is only a theory and frankly doesn't answer all the questions anyway, there could be room for them to consider some aspects of the expansion concept within it.
I put that poorly, I know, but for example, I wonder about this fact: our planet's rotational period is not constant. The general trend is that the rotation rate is slowing. I recall reading somewhere that back in the Devonian, the day was around 22 hours, by the Jurassic it had lengthened to 23 hours, because the Earth's rotation had slowed. (Note: the year was around the same, but it just had more days in it then than it does now.)
Now, it makes sense that as our planet is not a closed system (as we're travelling through space), forces acting on it will affect its rate of spin, and one could argue that these external factors are enough to slow down the spin. In fact it seems that generally, that's the argument -- along with energy loss from the planet. (Not sure if that works out but I recall reading it.)
Overall though, this external forces thing sounds fine, but on the other hand, have any detailed analyses been done to demonstrate that the rate of the Earth's slow down is totally accounted for by these factors? Because if the Earth is expanding -- even at an incredibly slow rate -- then the law of conservation of angular momentum has to be considered.
It states that a given mass moving around an axis at a certain rate will move more slowly if some of the mass is positioned further from the axis of rotation. (eg an ice skater doing a spin can slow down the spin quite rapidly by moving her arms out and speed up by moving them in close.)
Ergo, if the Earth is expanding even at a very slow rate, then with more mass further from the axis, it will slow down.
So, putting it simply: does the Earth's reducing rate of spin (over millions of years) correspond exactly to the known external forces acting on that could reduce its spin, when taken along with its energy loss? If not, then it's expanding.
I have no idea if it is or it isn't. My concern is that if it is, then it is something we'd have to consider in quake research.
And with that I really need to sign off. Good night
and stay safe...
Mikeedit on 18/9/11 by JustMike because: typ-o
Are things the way we've learned or is somehting else possible?
reply to post by MoparDanno
Yes, i was going to ask the same question, what happened to Venus on that aspect?
reply to post by TMJ1972
I've heard of that theory on why the earth spins, but i thought maybe there were other theories or speculations on that.
I asked that question while thinking of magnets and electricity. Lorentz force.
Maybe there is galactic current of some kind that we haven't measured yet and the interaction with the magnetic field lines pushes our planet in a spin?
On the other hand, the sun changes polarity every solar cycle but it don't changes it's rotation direction. But than it's not really a planet of course and don't know if that would make a difference.
Yes, i was going to ask the same question, what happened to Venus on that aspect?
reply to post by TMJ1972
I've heard of that theory on why the earth spins, but i thought maybe there were other theories or speculations on that.
I asked that question while thinking of magnets and electricity. Lorentz force.
Maybe there is galactic current of some kind that we haven't measured yet and the interaction with the magnetic field lines pushes our planet in a spin?
On the other hand, the sun changes polarity every solar cycle but it don't changes it's rotation direction. But than it's not really a planet of course and don't know if that would make a difference.
Going a couple of rungs up the ladder from planetary motion to galactic motion and thinking about some things I've been reading about, I decided to
look in the DOE's knowledge database and see if anything came up.
Imagine my surprise when I read the following in this abstract:
Ok, so as matter condenses it has, randomly distributed within it, areas of angular momenta (areas of spin) throughout. How does this relate to planetary motion?
In other words, from the tiniest scale imaginable (subatomic) to the largest (galactic super clusters), there are universal causes of motion.
From within the text of the document. This shows that prior to any matter formation (dark(if you subscribe to the theory) and baryonic) there are already properties of spin present.
So here they are asking the same question I had earlier, how has the energy of angular momentum been transferred away from a system's center to its constituent components?
Translation: Traditional models are not sufficient to explain the transport of angular momentum.
It seems to me that what is being said is that the initial spin in an area (existing before matter creation remember) plays a role in transporting angular momentum.
(continued)
Imagine my surprise when I read the following in this abstract:
It is suggested that star formation is organized following the same principles as we have applied in a recent explanation of galaxy and massive black hole formation. In this scenario angular momentum is randomly distributed by tidal torquing among condensations, Lyman-[alpha] clouds or cores for star formation during the initial non-linear phase of collapse.
Ok, so as matter condenses it has, randomly distributed within it, areas of angular momenta (areas of spin) throughout. How does this relate to planetary motion?
This parameter is calculated in very many simulations of structure formation of the universe as well as core formation and appears to be universal and independent of any scale.
In other words, from the tiniest scale imaginable (subatomic) to the largest (galactic super clusters), there are universal causes of motion.
emphasis mine
Furthermore the NFW distribution of dark matter has not yet formed, but the angular momentum of both the dark and baryonic matter has been set by previous tidal torquing events. (This implies that despite the usual calculations tha t determine X using dark matter, the result should be same for baryonic matter in core formation.)
From within the text of the document. This shows that prior to any matter formation (dark(if you subscribe to the theory) and baryonic) there are already properties of spin present.
In the black hole case the single unifiying principle of the RVI predicts not only this mass ratio, but the extraordinary correlation of BH mass with the velocity dispersion of stars surrounding the BH. The same principle can be applied to the stellar case with the prediction of the formation of a solar mass on average, and also the mass of a surrounding disk as well as a flat rotation velocity correlated with the mass of the collapsed star. Before deriving these relations, a discussion of the transport of angular momentum by the RVI and other possible mechanisms is considered.
So here they are asking the same question I had earlier, how has the energy of angular momentum been transferred away from a system's center to its constituent components?
There are a number of ways that have been suggested to transport the angular momentum: primarily by magnetic fields and the turbulence that is presumed to be generated by the magneto rotational instability, MRI. There are two problems with this explanation: no turbulent viscosity can work for the case of galactic BH formation because of the excessive mass of the disk, >> than the BH mass, necessary t o transport the angular momentum at near the Eddinton limit. In the case of a proto stellar disk, the low electrical conductivity of the near neutral gas a t low temperature, N 100 K , and with N mass fraction of dust. (The dust attaches and immobilizes the free ions from cosmic ray ionization.) The RVI circumvents both these problems and further predicts the masses and velocity dispersion
Translation: Traditional models are not sufficient to explain the transport of angular momentum.
Among various initial equilibria that we have examined, we generally find t h a t there are three stages of the disk evolution: (1) The exponential growth of the initial small amplitude perturbations are in excellent agreement with the linear theory. ( 2 ) The production of large scale vortices and their interactions with the background flow, including shocks. Significant accretion is observed due to these vortices. (3) The coupling of Rossby waves/vortices with global spiral waves, which facilitate further accretion throughout the whole disk. Even after more than 20 revolutions at the radius of the vortices, we find that the disk maintains a state that is populated with vortices, shocks, and spiral waves/shocks, all of which transport angular momentum outwards. We have shown that there is an efficient outward angular momentum transport in stages (2) and (3) ,over most parts of the disk, with an equivalent Shakura-Sunyaev angular momentum transport parameter a in the range from 10 [super-2] to 10 [super-4]. By carefully analyzing the flow structure around a vortex, we have shown how such vortices prove to be almost ideal “units” in transporting angular momentum outwards, namely by positively correlating the radial and azimuthal velocity component
It seems to me that what is being said is that the initial spin in an area (existing before matter creation remember) plays a role in transporting angular momentum.
(continued)
edit on 8-10-2011 by jadedANDcynical because: ladder, not latter... duh
reply to post by jadedANDcynical
(continued from previous post)
So we are left to wonder how it is that the study of angular momentum fits in with this:
Looking in the Cornell University Library e-print site we find this paper:
Which again is discussing higher dimensional effects upon our observable universe. The idea of higher dimensions existing without (that is "surrounding" our universe) is not a new one. Mystics have been telling us this is the case since before we had written language, science on the other hand, has taken a little longer to come to that conclusion:
And just why was this idea ignored for such a long time?
So, sticky, not easily answered or pigeon-holed questions arose, no wonder scientists shied away, but no more:
We all know that the littlest differences can have the most dramatic effects if applied in precisely the correct way in a specific location.
Ok, so how does all of this talk of higher dimensional energies relate to our universe?
stay tuned for part three...
(continued from previous post)
So we are left to wonder how it is that the study of angular momentum fits in with this:
source
The mission of the Energy Department is to ensure America’s security and prosperity by addressing its energy, environmental and nuclear challenges through transformative science and technology solutions.
Looking in the Cornell University Library e-print site we find this paper:
We revisit the Riemann-Cartan geometry in the context of recent higher-dimensional theories of spacetime. After introducing the concept of torsion in a modern geometrical language we present some results that represent extensions of Riemannian theorems. We consider the theory of local embeddings and submanifolds in the context of Riemann-Cartan geometries and show how a Riemannian spacetime may be locally and isometrically embedded in a bulk with torsion. As an application of this result, we discuss the problem of classical confinement and the stability of motion of particles and photons in the neighbourhood of branes for the case when the bulk has torsion. We illustrate our ideas considering the particular case when the embedding space has the geometry of a warped product space . We show how the confinement and stability properties of geodesics near the brane may be affected by the torsion of the embedding manifold. In this way we construct a classical analogue of quantum confinement inspired in theoretical-field models by replacing a scalar field with a torsion field.
Which again is discussing higher dimensional effects upon our observable universe. The idea of higher dimensions existing without (that is "surrounding" our universe) is not a new one. Mystics have been telling us this is the case since before we had written language, science on the other hand, has taken a little longer to come to that conclusion:
The idea that our spacetime may have more than four dimensions seems to be a recurrent theme in contemporary theoretical physics research. Such idea was first conjectured by G. Nordstrom [1], in 1914 (before the completion of general relativity), whose aim was to achieve unification of gravity with electromagnetism. Although Nordstrom’s interesting work, done in the context of a scalar gravity theory, was ignored for a long time, the same basic idea was taken up again, a few years later, by the mathematician T. Kaluza [2]
And just why was this idea ignored for such a long time?
In almost all theories mentioned above it has been generally assumed that the underlying higher-dimensional space (often referred to as the bulk [7]) has a Riemannian character. Surely this is the more natural assumption to be made since the Riemannian theory is the geometrical setting of the well-established theory of general relativity. With very few exceptions, there has not been much discussion on whether the bulk could admit more general geometries.
So, sticky, not easily answered or pigeon-holed questions arose, no wonder scientists shied away, but no more:
In spite of the limited interest it has arisen among theoretical physicists since its conception (perhaps due to the fact that it differs very little from general relativity), some authors believe that the Einstein-Cartan theory can have an important role in a future quantum theory of gravitation [16]. Moreover, torsion cosmology has been investigated recently in connection with the acceleration of the Universe [17]
We all know that the littlest differences can have the most dramatic effects if applied in precisely the correct way in a specific location.
Ok, so how does all of this talk of higher dimensional energies relate to our universe?
One of the motivations for studying the geodesic motion in the presence of torsion is the following. As is well known, in the brane-world scenario the stability of the confinement of matter fields at the quantum level is made possible by assuming an interaction of matter with a scalar field. An example of how this mechanism works is nicely illustrated by a field-theoretical model devised by Rubakov, in which fermions may be trapped to a brane by interacting with a scalar field that depends only on the extra dimension [13]. On the other hand, the kind of confinement we are concerned with is purely geometrical, and that means the only force acting on the particles is the gravitational force. In a purely classical (non-quantum) picture, one would like to have effective mechanisms, other than the presence of a quantum scalar field, to constrain massive particles to move on hypersurfaces in a stable way
stay tuned for part three...
reply to post by jadedANDcynical
(part three) I really HATE these post limits...
Hold on a moment!
Does that paper really say "scalar field?"
You mean like non-existent scalar weapons?
Yep, it is discussing a scalar (higher dimensional) energy field...
Anyway, what does this talk of torsion have to do with spin in general and celestial motion in specific?
Without torsion we would have the following motion:
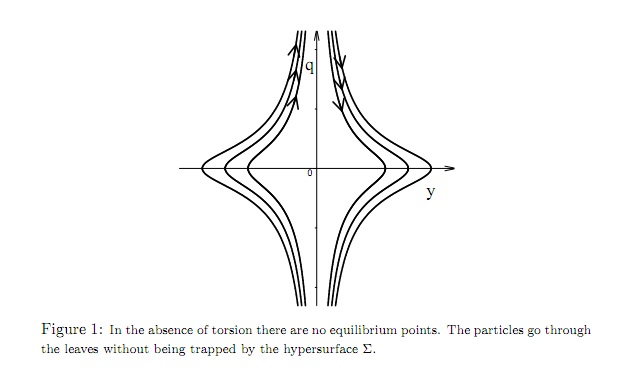
If we include the existence of a torsion field, we get this:
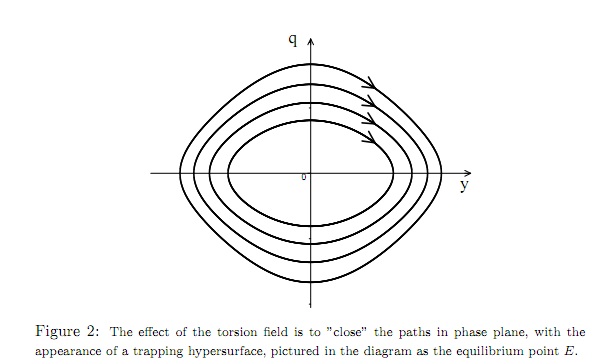
So it would seem that the inclusion of a torsion filed (a non-local all-present energy field "outside" our universe) fits with what is observed in our universe..
more
It seems that there are situations in which the spin from the higher dimension is not transferred to our universe thus leaving it in potential. Is this potential what is targeted in researching zero point energy?
Food for thought in any case...
(part three) I really HATE these post limits...
Hold on a moment!
Does that paper really say "scalar field?"
You mean like non-existent scalar weapons?
Two possibilities of implement such a program have already been studied. One is to assume a direct interaction between the particles and a physical scalar field [25]. Following this approach it has been shown that stable confinement in a thick brane is possible by means of a direct interaction of the particles with a scalar field through a modification of the Lagrangian of the particle. A second approach would appeal to pure geometry: for instance, modelling the bulk with a Weyl geometrical structure. In this case it is the Weyl field that provides the mechanism necessary for confinement and stabilization of the motion of particles in the brane [14]. At this stage, we would like to know whether classical confinement of particles and photons could also be obtained by using a torsion field, that is, by allowing for the bulk to have a Riemann-Cartan geometry.
Yep, it is discussing a scalar (higher dimensional) energy field...
Anyway, what does this talk of torsion have to do with spin in general and celestial motion in specific?
Without torsion we would have the following motion:

If we include the existence of a torsion field, we get this:

So it would seem that the inclusion of a torsion filed (a non-local all-present energy field "outside" our universe) fits with what is observed in our universe..
We have shown that for a class of torsion fields, the geometry induced on four-dimensional spacetime has a Riemannian structure. This means that it is possible to embed isometrically a Riemannian spacetime into a Riemann-Cartan five-dimensional bulk with non-vanishing torsion. We also have shown that confinement and stability properties of geodesics near the brane may be affected by the torsion.
more
Transposing these ideas to the Einstein-Cartan theory of gravity, one would naturally wonder whether spin could also be generated, or induced, in the same manner, from a higher-dimensional space. The results obtained in Sec. 3, allow us to draw some conclusions in this respect. One is that if the bulk M is a torsionless space ( hence not sourced by matter with spin), then it is not possible to generate spin geometrically (through dimensional reduction) in the four-dimensional spacetime M. A second conclusion is that, in general, spin in four dimensions may be generated from five dimensions, but in some particular cases the bulk does not transfer spin to four-dimension.
It seems that there are situations in which the spin from the higher dimension is not transferred to our universe thus leaving it in potential. Is this potential what is targeted in researching zero point energy?
Food for thought in any case...
edit on 8-10-2011 by jadedANDcynical because: close parenthesis
reply to post by jadedANDcynical
No.
Not like non-existent scalar weapons. A scalar field has nothing to do with "scalar waves" (which do not exist as claimed). It is a way of defining a property of each point in a given space. You can have a scalar field for temperature, or magnetic field strength, or pressure, or any other property.
en.wikipedia.org...
Does that paper really say "scalar field?"
You mean like non-existent scalar weapons?
No.
Not like non-existent scalar weapons. A scalar field has nothing to do with "scalar waves" (which do not exist as claimed). It is a way of defining a property of each point in a given space. You can have a scalar field for temperature, or magnetic field strength, or pressure, or any other property.
en.wikipedia.org...
edit on 10/8/2011 by Phage because: (no reason given)
reply to post by Phage
That isn't what is discussed here:
Or here
?
That isn't what is discussed here:
We use data on the local 3-dimensional galaxy distribution for studying the statistics of the detection rates of gravitational waves (GW) coming from supernova explosions. We consider both tensor and scalar gravitational waves which are possible in a wide range of relativistic and quantum gravity theories. We show that statistics of GW events as a function of sidereal time can be used for distinction between scalar and tensor gravitational waves because of the anisotropy of spatial galaxy distribution. For calculation of the expected amplitudes of GW signals we use the values of the released GW energy, frequency and duration of GW pulse which are consistent with existing scenarios of SN core collapse. The amplitudes of the signals produced by Virgo and the Great Attractor clusters of galaxies is expressed as a function of the sidereal time for resonant bar detectors operating now (IGEC) and for forthcoming laser interferometric detectors (VIRGO).Then, we calculate the expected number of GW events as a function of sidereal time produced by all the galaxies within 100 Mpc. In the case of axisymmetric rotational core collapse which radiates a GW energy of $10^[-9]M_[\odot]c^2$, only the closest explosions can be detected. However, in the case of nonaxisymmetric supernova explosion, due to such phenomena as centrifugal hangup, bar and lump formation, the GW radiation could be as strong as that from a coalescing neutron-star binary. For radiated GW energy higher than $10^[-6]M_[\odot]c^2$ and sensitivity of detectors at the level $h \approx 10^[-23]$ it is possible to detect Virgo cluster and Great Attractor, and hence to use the statistics of GW events for testing gravity theories.
Or here
?
reply to post by jadedANDcynical
Most everything I've seen claimed about "scalar weapons" is that they involve some sort of electromagnetic radiation, which is an oxymoron. Electromagnetic radiation consists of transverse waves not longitudinal (scalar) waves.
Are you suggesting that "scalar weapons" use gravitational waves? Which is what your first source is talking about. It's talking about waves moving through a scalar gravity field.
Are you suggesting that "scalar weapons" use sound waves? Which is what your second source is talking about. It's talking about density waves moving through air (a scalar field).
www.amazon.com...
Most everything I've seen claimed about "scalar weapons" is that they involve some sort of electromagnetic radiation, which is an oxymoron. Electromagnetic radiation consists of transverse waves not longitudinal (scalar) waves.
Are you suggesting that "scalar weapons" use gravitational waves? Which is what your first source is talking about. It's talking about waves moving through a scalar gravity field.
Are you suggesting that "scalar weapons" use sound waves? Which is what your second source is talking about. It's talking about density waves moving through air (a scalar field).
This monograph is an excellent introduction to the mathematical techniques used to describe the scattering and propagation of scalar waves, in particular sound waves.
www.amazon.com...
reply to post by Phage
I've read a great deal on what scalar technology is, and the frequency science it is. No time for this thread,for me to be stuck in the hours of research. I highly recommend it to everyone to do this research themselves. It has a lot of potential for harm. One scientist showed in a lab setting, in a covered glass container, basically what scalar waves can do to Clouds, and the Ionsphere, and how it lifts it up. It can create rain/floods, and drought. Not to mention earthquakes and all sorts of things.
I even wonder if it has something to do with the core and sudden increase in the polar wander.
Not only that, but there are patents out for much more powerful systems.
I was told by someone, that the only reason they keep the over unity away from people, and clean cheap/free energy is GREED. That doesnt' cause problems. But scalar would need to be controlled by higher levels, because its relatively simple, and could be used in gang warfare in very bad ways. ie. you take revenge on the competition by destroying his home city. Not safe to have out on the streets.
But unfortunately, we already have it in the hands of the worst bullies in the cosmos nearly, just a step up from the abyss.
I've read a great deal on what scalar technology is, and the frequency science it is. No time for this thread,for me to be stuck in the hours of research. I highly recommend it to everyone to do this research themselves. It has a lot of potential for harm. One scientist showed in a lab setting, in a covered glass container, basically what scalar waves can do to Clouds, and the Ionsphere, and how it lifts it up. It can create rain/floods, and drought. Not to mention earthquakes and all sorts of things.
I even wonder if it has something to do with the core and sudden increase in the polar wander.
Not only that, but there are patents out for much more powerful systems.
I was told by someone, that the only reason they keep the over unity away from people, and clean cheap/free energy is GREED. That doesnt' cause problems. But scalar would need to be controlled by higher levels, because its relatively simple, and could be used in gang warfare in very bad ways. ie. you take revenge on the competition by destroying his home city. Not safe to have out on the streets.
But unfortunately, we already have it in the hands of the worst bullies in the cosmos nearly, just a step up from the abyss.
edit on 8-10-2011
by Unity_99 because: (no reason given)
new topics
-
MH370 Again....
Disaster Conspiracies: 25 minutes ago -
Are you ready for the return of Jesus Christ? Have you been cleansed by His blood?
Religion, Faith, And Theology: 2 hours ago -
Chronological time line of open source information
History: 4 hours ago -
A man of the people
Diseases and Pandemics: 5 hours ago -
Ramblings on DNA, blood, and Spirit.
Philosophy and Metaphysics: 5 hours ago -
4 plans of US elites to defeat Russia
New World Order: 7 hours ago -
Thousands Of Young Ukrainian Men Trying To Flee The Country To Avoid Conscription And The War
Other Current Events: 10 hours ago
top topics
-
Israeli Missile Strikes in Iran, Explosions in Syria + Iraq
World War Three: 14 hours ago, 17 flags -
Thousands Of Young Ukrainian Men Trying To Flee The Country To Avoid Conscription And The War
Other Current Events: 10 hours ago, 7 flags -
Iran launches Retalliation Strike 4.18.24
World War Three: 13 hours ago, 6 flags -
12 jurors selected in Trump criminal trial
US Political Madness: 13 hours ago, 4 flags -
4 plans of US elites to defeat Russia
New World Order: 7 hours ago, 4 flags -
A man of the people
Diseases and Pandemics: 5 hours ago, 3 flags -
Chronological time line of open source information
History: 4 hours ago, 2 flags -
Are you ready for the return of Jesus Christ? Have you been cleansed by His blood?
Religion, Faith, And Theology: 2 hours ago, 1 flags -
Ramblings on DNA, blood, and Spirit.
Philosophy and Metaphysics: 5 hours ago, 1 flags -
MH370 Again....
Disaster Conspiracies: 25 minutes ago, 0 flags
active topics
-
Israeli Missile Strikes in Iran, Explosions in Syria + Iraq
World War Three • 72 • : DBCowboy -
Fossils in Greece Suggest Human Ancestors Evolved in Europe, Not Africa
Origins and Creationism • 67 • : strongfp -
Thousands Of Young Ukrainian Men Trying To Flee The Country To Avoid Conscription And The War
Other Current Events • 16 • : Cvastar -
Are you ready for the return of Jesus Christ? Have you been cleansed by His blood?
Religion, Faith, And Theology • 10 • : TruthJava -
Not Aliens but a Nazi Occult Inspired and then Science Rendered Design.
Aliens and UFOs • 13 • : Ophiuchus1 -
12 jurors selected in Trump criminal trial
US Political Madness • 36 • : Cvastar -
MH370 Again....
Disaster Conspiracies • 0 • : Cvastar -
So I saw about 30 UFOs in formation last night.
Aliens and UFOs • 34 • : Arbitrageur -
4 plans of US elites to defeat Russia
New World Order • 27 • : andy06shake -
ChatGPT Beatles songs about covid and masks
Science & Technology • 22 • : iaylyan
