It looks like you're using an Ad Blocker.
Please white-list or disable AboveTopSecret.com in your ad-blocking tool.
Thank you.
Some features of ATS will be disabled while you continue to use an ad-blocker.
9
share:
Being a web/graphics designer I come across a lot of crazy designs created by math. We have fractal art which is amazing:

Then we have the Mandlebot/Mandlebulb which is an entire 3-dimensional "world" created from math.

All of the images below come from the above object. Look at the one with what looks like stars on the right-my fav.

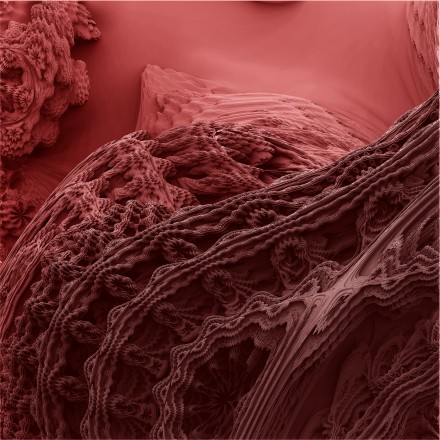
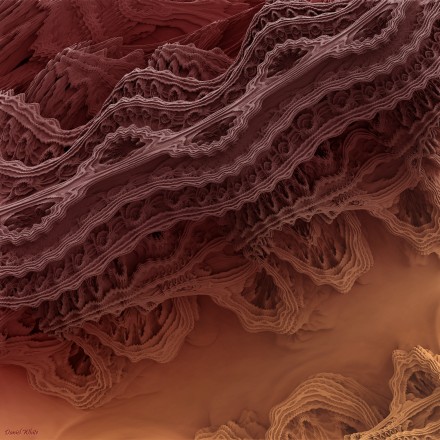





An awesome video inside the Mandlebulb:
Link:www.skytopia.com...
Hope you enjoyed!

Then we have the Mandlebot/Mandlebulb which is an entire 3-dimensional "world" created from math.
TIMESTAMP 08/11/2009. The original Mandelbrot is an amazing object that has captured the public's imagination for 30 years with its cascading patterns and hypnotically colourful detail. It's known as a 'fractal' - a type of shape that yields (sometimes elaborate) detail forever, no matter how far you 'zoom' into it (think of the trunk of a tree sprouting branches, which in turn split off into smaller branches, which themselves yield twigs etc.).
It's found by following a relatively simple math formula. But in the end, it's still only 2D and flat - there's no depth, shadows, perspective, or light sourcing. What we have featured in this article is a potential 3D version of the same fractal. For the impatient, you can skip to the nice pics, but the below makes an interesting read (with a little math as well for the curious).

All of the images below come from the above object. Look at the one with what looks like stars on the right-my fav.








An awesome video inside the Mandlebulb:
What's the formula of this thing?
There are a few subtle variations, which mostly end up producing the same kind of incredible detail. Listed below is one version. Similar to the original 2D Mandelbrot, the 3D formula is defined by:
z -> z^n + c
...but where 'z' and 'c' are hypercomplex ('triplex') numbers, representing Cartesian x, y, and z coordinates. The exponentiation term can be defined by:
[x,y,z]^n = r^n [ sin(theta*n) * cos(phi*n) , sin(theta*n) * sin(phi*n) , cos(theta*n) ]
...where:
r = sqrt(x^2 + y^2 + z^2)
theta = atan2( sqrt(x^2+y^2), z )
phi = atan2(y,x)
And the addition term in z -> z^n + c is similar to standard complex addition, and is simply defined by:
[x,y,z]+[a,b,c] = [x+a, y+b, z+c]
The rest of the algorithm is similar to the 2D Mandelbrot!
Here is some pseudo code of the above:
r = sqrt(x*x + y*y + z*z )
theta = atan2(sqrt(x*x + y*y) , z)
phi = atan2(y,x)
newx = r^n * sin(theta*n) * cos(phi*n)
newy = r^n * sin(theta*n) * sin(phi*n)
newz = r^n * cos(theta*n)
...where n is the order of the 3D Mandelbulb. Use n=8 to find the exact object in this article.
Link:www.skytopia.com...
Hope you enjoyed!
edit on 25-9-2011 by samlf3rd because: (no reason given)
edit on 25-9-2011 by samlf3rd because: (no reason
given)
edit on 25-9-2011 by samlf3rd because: Uploaded images properly
edit on 25-9-2011 by samlf3rd because: (no
reason given)
totally incredible!!! i loved this so beautiful,and so bizzar at the same time. i fell in love with fractal art 20 + years og,but i've never
seen 3-D fractals before! totally cool
reply to post by reficul
I know I want to get the program, I do use Apophisys, which is very awesome:apophysis.org...
That will keep you busy for a few years. Play with the attributes and go to town. The trick is to open the triangle editor-move them around, change their shape, create new ones, overlap them and wait a long long time to see the results. My son made a 3d tube somehow, it's now my desktop background.
I know I want to get the program, I do use Apophisys, which is very awesome:apophysis.org...
That will keep you busy for a few years. Play with the attributes and go to town. The trick is to open the triangle editor-move them around, change their shape, create new ones, overlap them and wait a long long time to see the results. My son made a 3d tube somehow, it's now my desktop background.
Here is a list of many different types of fractal programs, even for Mac's yeah!
fractalfoundation.org...
fractalfoundation.org...
edit on 25-9-2011 by samlf3rd because: (no reason given)
reply to post by samlf3rd
Beautiful pics. Look up "Fourier" calculus to see the link between this and our brains.
Beautiful pics. Look up "Fourier" calculus to see the link between this and our brains.
I am studying organic chemistry at the moment and while looking at this I am wondering...
...if it would be possible to plot the energy levels of the (infinite number of) organic compounds in this way. it makes a lot of sense that the distribution of energy in the universe would follow this type of plot.
so, in other words, when looking at the mandelbulb, all of the large and /or repetitive structures would represent stable compounds. and the chaotic areas would represent the energetic transitions between the compounds.
in fact, it makes so much sense, I cannot be the first person to have thought of it.
thanks for posting!
...if it would be possible to plot the energy levels of the (infinite number of) organic compounds in this way. it makes a lot of sense that the distribution of energy in the universe would follow this type of plot.
so, in other words, when looking at the mandelbulb, all of the large and /or repetitive structures would represent stable compounds. and the chaotic areas would represent the energetic transitions between the compounds.
in fact, it makes so much sense, I cannot be the first person to have thought of it.
thanks for posting!
reply to post by tgidkp
As I look at these pics and the video I wonder if this is the easiest way to describe the universe. Infinity explained visually? It never ends, because the math is infinite, like space and time.
As I look at these pics and the video I wonder if this is the easiest way to describe the universe. Infinity explained visually? It never ends, because the math is infinite, like space and time.
reply to post by tgidkp
You aren't the first to think of it, nope... however don't let that discourage you. We need more people thinking this way so let it shine!
Namaste!
You aren't the first to think of it, nope... however don't let that discourage you. We need more people thinking this way so let it shine!
Namaste!
Evasius already made a thread on this ;
www.abovetopsecret.com...
Just pointing that out for those who didn't know.
www.abovetopsecret.com...
Just pointing that out for those who didn't know.
new topics
-
2024 Pigeon Forge Rod Run - On the Strip (Video made for you)
Automotive Discussion: 31 minutes ago -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues: 57 minutes ago -
The functionality of boldening and italics is clunky and no post char limit warning?
ATS Freshman's Forum: 2 hours ago -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News: 2 hours ago -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest: 2 hours ago -
Weinstein's conviction overturned
Mainstream News: 4 hours ago -
Supreme Court Oral Arguments 4.25.2024 - Are PRESIDENTS IMMUNE From Later Being Prosecuted.
Above Politics: 5 hours ago -
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest: 5 hours ago -
Chris Christie Wishes Death Upon Trump and Ramaswamy
Politicians & People: 6 hours ago -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media: 8 hours ago
top topics
-
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest: 5 hours ago, 8 flags -
Weinstein's conviction overturned
Mainstream News: 4 hours ago, 6 flags -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media: 8 hours ago, 5 flags -
Supreme Court Oral Arguments 4.25.2024 - Are PRESIDENTS IMMUNE From Later Being Prosecuted.
Above Politics: 5 hours ago, 5 flags -
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest: 2 hours ago, 4 flags -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News: 2 hours ago, 4 flags -
Any one suspicious of fever promotions events, major investor Goldman Sachs card only.
The Gray Area: 10 hours ago, 2 flags -
Chris Christie Wishes Death Upon Trump and Ramaswamy
Politicians & People: 6 hours ago, 2 flags -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues: 57 minutes ago, 2 flags -
God's Righteousness is Greater than Our Wrath
Religion, Faith, And Theology: 15 hours ago, 1 flags
active topics
-
Massachusetts Drag Queen Leads Young Kids in Free Palestine Chant
Social Issues and Civil Unrest • 9 • : theatreboy -
Meadows, Giuliani Among 11 Indicted in Arizona in Latest 2020 Election Subversion Case
Mainstream News • 5 • : Disgusted123 -
Candidate TRUMP Now Has Crazy Judge JUAN MERCHAN After Him - The Stormy Daniels Hush-Money Case.
Political Conspiracies • 774 • : Oldcarpy2 -
God's Righteousness is Greater than Our Wrath
Religion, Faith, And Theology • 29 • : Topcraft -
2024 Pigeon Forge Rod Run - On the Strip (Video made for you)
Automotive Discussion • 4 • : TheInvisibleRedneck -
Gaza Terrorists Attack US Humanitarian Pier During Construction
Middle East Issues • 11 • : JAY1980 -
Chris Christie Wishes Death Upon Trump and Ramaswamy
Politicians & People • 18 • : FlyersFan -
Breaking Baltimore, ship brings down bridge, mass casualties
Other Current Events • 488 • : xuenchen -
Krystalnacht on today's most elite Universities?
Social Issues and Civil Unrest • 3 • : StudioNada -
University of Texas Instantly Shuts Down Anti Israel Protests
Education and Media • 178 • : theatreboy
9


