There's no need for Wave Function collapse or Measurement in Quantum Mechanics

The idea of wave function collapse and measurement has caused so many unnecessary problems when it comes to Quantum Mechanics. Both of these things are nowhere in the theory; they're just postulated because you have a wave function of a quantum system that consists of probable states the particle can be in and once you have knowledge of the state the probabilities go away. Now you’re left with a single state. Scientists assumed there must be collapse of the wave function caused by a measurement.

This leads us to two central problems with Quantum Mechanics. How do you explain wave function collapse and the measurement problem? The problem, no pun intended, is that neither of these things are anywhere in the theory of Quantum Mechanics. Again, they’re just postulated in an ad hoc way to explain features that we see in experiments on quantum systems.

There’s a simple yet elegant answer to this. It’s found in the Relational interpretation of Quantum Mechanics and the recent Wigner’s friend experiment.

Simply, no collapse or measurement occurs. Here’s an explanation from Relational Quantum Mechanics that’s just mind blowing.

All physical interactions are, at bottom, quantum interactions, and must ultimately be governed by the same rules. Thus, an interaction between two particles does not, in RQM, differ fundamentally from an interaction between a particle and some "apparatus". There is no true wave collapse, in the sense in which it occurs in the Copenhagen interpretation.

Because "state" is expressed in RQM as the correlation between two systems, there can be no meaning to "self-measurement". If observer O measures system S, S's "state" is represented as a correlation between O and S. O itself cannot say anything with respect to its own "state", because its own "state" is defined only relative to another observer, O'. If the S+O compound system does not interact with any other systems, then it will possess a clearly defined state relative to O'. However, because O's measurement of S breaks its unitary evolution with respect to O, O will not be able to give a full description of the S+O system (since it can only speak of the correlation between S and itself, not its own behaviour). A complete description of the (S+O)+O' system can only be given by a further, external observer, and so forth.

Taking the model system discussed above, if O' has full information on the S+O system, it will know the Hamiltonians of both S and O, including the interaction Hamiltonian. Thus, the system will evolve entirely unitarily (without any form of collapse) relative to O', if O measures S. The only reason that O will perceive a "collapse" is because O has incomplete information on the system (specifically, O does not know its own Hamiltonian, and the interaction Hamiltonian for the measurement).

en.wikipedia.org...

What this says is that wave function collapse and what’s called self measurement doesn’t occur. What we call measurement isn’t a problem. It’s just some observer gaining information about a quantum system. The problem occurs because people assume a measurement must cause “collapse” even though this isn’t anywhere to be found in Quantum Mechanics or Quantum Field Theory.

So an observer gains knowledge about the quantum system and it’s wave function just expands to include the observer's obtaining knowledge. So an observer that’s entangled with the wave function of the quantum system can’t measure interference because he or she is a part of the entire system described by the wave function. So Schrodinger’s cat is alive and dead.

Now, an observer O’ that’s external to the S+O system in the lab in the case of Wigner’s friend, is a quantum system and Wigner can do an interference measurement and see his friend, the system and the lab in a superposition of both states.

So the wave function never collapses. Here’s an example.

Wigner’s friend is in the lab carrying out the double slit experiment. The friend sees interference when a photon gun is shooting photons at the two slits.

The friend puts an apparatus next to one of the slits to obtain which path information. The photon behaves like a particle now. This isn’t due to collapse but now the wave function extends to the apparatus next to the slit. The friend gains knowledge about the system and now the wave function extends to the friend and the lab.

No collapse or measurement to cause collapse. The friend sees a classical particle because he’s now a part of the wave function of the quantum system and him, the apparatus and the lab in a superposition of all measurements that can occur.

Wigner outside the lab can confirm this by doing an interference measurement on the results and the system. So Wigner acts as a super observer O’ that can measure and see interference between S+O in the lab.

This has profound implications because it shows, different observers can reach different outcomes of an event. It also shows that a system whether quantum or classical in size is never in a state of collapse. They’re always entangled with some wave function.

What does this show about parallel universes? Say Wigner’s friend is measuring the polarization of a photon. He starts with the wave function that says photon is vertical/photon is horizontal. When he carries out a measurement he only sees a result locally from his frame of reference which is that the photon is vertical or the photon is horizontal. Both of these states exist in superposition but each friend can only measure the state in his or her frame of reference. Wigner outside can measure both states and see interference.

Now, Wigner finds out the results. He’s now part of the system and there’s 2 Wigner’s. One who’s in a universe where his friend measures v and one where his friend measures h. Wigner’s Uncle can act as a super observer and measure interference between all 4 states. These 2 states, Wigner+friend v and Wigner+friend h will eventually decohere and evolve as two separate universes.

So what we call a measurement is observer dependent and is relative to the frame of reference(lab in this case) between S and O.

So this interpretation treats collapse and measurement like Einstein treats the distinction between past, present and future. These things are both relative to the observer’s frame of reference.

a reply to: neoholographic

But why so complicated? The wavefunction y(t;v) collapses because you pick a point t when you measure, because you know t you lose the possibility to know v that's just how the uncertainty principle works.
I don't see why that would be a problem? Why I have to invent a system plus observer, plus observer' ....


Think of the little fermion moving around, doing its wave business, if you want to know how fast and which direction it's going you can't nail it to one place because that would mean it loses what you want to know about it. You have to allow for a certain period of t and live with the fact that there's a certain area where it might have been. Now you want to know where it was at the point t: you have to nail it down.
That doesn't do anything to the fermion itself it's just the information you extract.
A wave is some type of movement in time, a function. If you set a point on the t axis as n it "collapses" because you make the description of the movement a simple coordinate. It's no longer a wave function.
And if you invent millions of additional observers it doesn't change that fact.

Also of course the measurement is relative to the one doing the experiment, they could hardly measure what's happening outside of their experiment so... wtf? How is that a statement worth making?

Personally I love physics, I love maths, deepest respect for everybody who's smart enough to do it (I'm just a observer) but
If you have to invent 11 dimensions and parallel universes and that at each point a decision is made you split up into infinity... that's maybe good for mental masturbation, but it's not science.

a reply to: Peeple

You said:

Also of course the measurement is relative to the one doing the experiment, they could hardly measure what's happening outside of their experiment so... wtf? How is that a statement worth making?

That statement is the key. It's saying whether QM is observer dependent or observer independent.

Wigner's friend is observer dependent. Here's the paper that confirmed Wigner's friend on microscopic scales.

Experimental test of local observer independence

The scientific method relies on facts, established through repeated measurements and agreed upon universally, independently of who observed them. In quantum mechanics the objectivity of observations is not so clear, most markedly exposed in Wigner’s eponymous thought experiment where two observers can experience seemingly different realities. The question whether the observers’ narratives can be reconciled has only recently been made accessible to empirical investigation, through recent no-go theorems that construct an extended Wigner’s friend scenario with four observers. In a state-of-the-art six-photon experiment, we realize this extended Wigner’s friend scenario, experimentally violating the associated Bell-type inequality by five standard deviations. If one holds fast to the assumptions of locality and free choice, this result implies that quantum theory should be interpreted in an observer-dependent way.

advances.sciencemag.org...

What this shows is that what we call wave function collapse and measurement is relative to the observer. So there's only measurement and collapse in the lab because the friend becomes entangled with the wave function of the quantum system. For Wigner outside the lab, it doesn't collapse and he can still measure interference.

This is vs. observer independence which pushes things like a universal wave function. So independent of observation, the universal wave function is the same for all observers,

This is a huge difference between a Relational interpretation of QM and Many Worlds. Many Worlds is observer independent and independent of the observer there's a universal wave function.

The Relational interpretation is observer dependent and says there isn't a universal wave function. Rovelli applies Relativity to QM in this way. He says there's no absolute or universal wave function so a measurement just like time is relative to the observer's frame of reference.

Like I said, that's a huge difference.

a reply to: neoholographic

But you still didn't understand that the wave function collapse is an experimental process and not a property of the wave.

Think of a beam of light you got a stream of photons each on their own oscillating in a nice sinus wave through the room and I got that recorded with super (hypothetical) hightech equipment, every three-ish metres every 10^-8 seconds a frame. In between the frames all I know is the photon I'm observing is moving in that direction with its speed. But each frame equals an observer because there is no more wave, there's just a "picture" of a certain light package at a certain place at a certain time.

That doesn't collapse the lightbeam, just my mathmatical prediction turns from a wave with amplitude, frequency etc into "3rd frame; t=10^-6" coordinates.
The observer is just a certain point in time and space.
The collapse more or less a derivative of the wave function for the purpose of extracting information.

I'm going to go with the many scientists that disagree...

a reply to: neoholographic

Imagine a four person tug-of-war between Einstein, Heisenberg, Schrodinger and Tesla.
Ramanujan is the referee, just for added 'clarity'.
In the end, everybody's got a piece of the rope but nobody "wins".

ganjoa

originally posted by: hombero
I'm going to go with the many scientists that disagree...

a reply to: neoholographic

That's a loaded statement...scientists don't even agree with each other on this subject. Not even 50% of the physicists polled believed the Copenhagen interpretation taught in textbooks is correct (which teaches wave function collapse).

A Snapshot of Foundational Attitudes Toward Quantum Mechanics

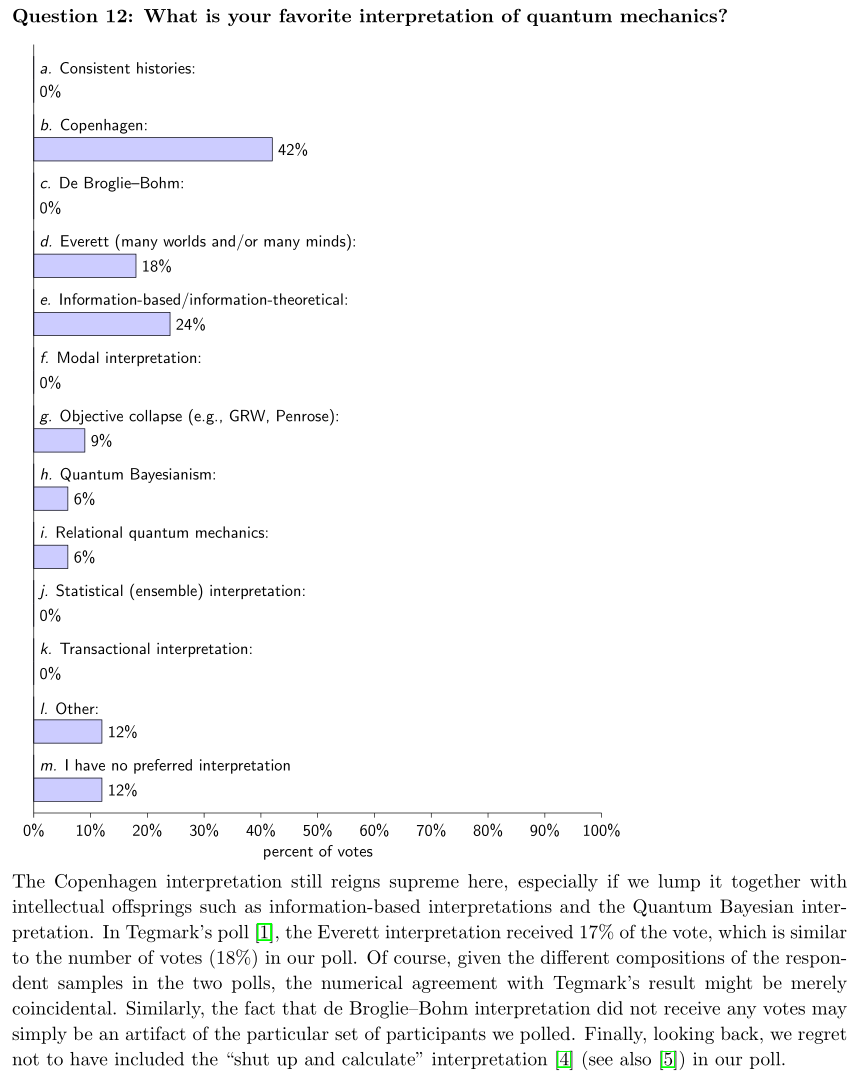
The sample size was small so the percentages are not a rigorous projection for the scientific community, but the idea that scientists don't agree on this topic is hard to argue with.

See "i. Relational quantum mechanics" in the graph. The 2011 poll shows 6% of the participants favoring the Relational quantum mechanics interpretation which is the topic of this thread.

The wikipedia link neo posted should be close enough for government work, but when neoholographic starts ad-libbing his own perceptions, I would take anything he says with a huge grain of salt.

originally posted by: neoholographic
Simply, no collapse or measurement occurs. Here’s an explanation from Relational Quantum Mechanics that’s just mind blowing.

That's a possibility, that no collapse occurs, but we don't really know. According to the 2011 poll, the highest percentage of responses (42%) believe it does (per the Copenhagen interpretation), but there are plenty who believe in alternate ideas where the wave function doesn't collapse. So far, nobody has been able to prove which interpretation is right, so these are competing ideas without conclusive proof until someone can come up with proof of which interpretation is correct.

a reply to: neoholographic

All physical interactions are, at bottom, quantum interactions, and must ultimately be governed by the same rules.

Says who ??

Someone who invented the theory ?
Or someone who believes it, right ??

This statement is actually implying that there is nothing else to think as that this, what quantum mechanics theory says is true.

I will not try to talk you out of this nonsense.. this theory is not just not correct, it is not even wrong !

simply said.. there is no wave function, there is no photon travelling, there is no quanta !!

a reply to: Bandu

Give me a break!

If you have a better theory than Quantum Theory that has given us the modern world we live in and is the most accurate theory we have to date, then get published and win a Nobel Prize.

Why should anyone accept your ramblings? You said:

simply said.. there is no wave function, there is no photon travelling, there is no quanta !!

If there's no wave function, explain this to me Einstein.

The wave-function is real but nonphysical: A view from counterfactual quantum cryptography

Counterfactual quantum cryptography (CQC) is used here as a tool to assess the status of the quantum state: Is it real/ontic (an objective state of Nature) or epistemic (a state of the observer's knowledge)? In contrast to recent approaches to wave function ontology, that are based on realist models of quantum theory, here we recast the question as a problem of communication between a sender (Bob), who uses interaction-free measurements, and a receiver (Alice), who observes an interference pattern in a Mach-Zehnder set-up. An advantage of our approach is that it allows us to define the concept of "physical", apart from "real". In instances of counterfactual quantum communication, reality is ascribed to the interaction-freely measured wave function (ψ) because Alice deterministically infers Bob's measurement. On the other hand, ψ does not correspond to the physical transmission of a particle because it produced no detection on Bob's apparatus. We therefore conclude that the wave function in this case (and by extension, generally) is real, but not physical. Characteristically for classical phenomena, the reality and physicality of objects are equivalent, whereas for quantum phenomena, the former is strictly weaker. As a concrete application of this idea, the nonphysical reality of the wavefunction is shown to be the basic nonclassical phenomenon that underlies the security of CQC.

arxiv.org...


Direct counterfactual communication via quantum Zeno effect

Significance

Recent theoretical studies have shown that quantum mechanics allows counterfactual communication, even without actual transmission of physical particles, which raised a heated debate on its interpretation. Although several papers have been published on the theoretical aspects of the subject, a faithful experimental demonstration is missing. Here, by using the quantum Zeno effect and a single-photon source, direct communication without carrier particle transmission is implemented successfully. We experimentally demonstrate the feasibility of direct counterfactual communication with the current technique. The results of our work can help deepen the understanding of quantum mechanics. Furthermore, our experimental scheme is applicable to other quantum technologies, such as imaging and state preparation.

Abstract

Intuition from our everyday lives gives rise to the belief that information exchanged between remote parties is carried by physical particles. Surprisingly, in a recent theoretical study [Salih H, Li ZH, Al-Amri M, Zubairy MS (2013) Phys Rev Lett 110:170502], quantum mechanics was found to allow for communication, even without the actual transmission of physical particles. From the viewpoint of communication, this mystery stems from a (nonintuitive) fundamental concept in quantum mechanics—wave-particle duality. All particles can be described fully by wave functions. To determine whether light appears in a channel, one refers to the amplitude of its wave function. However, in counterfactual communication, information is carried by the phase part of the wave function. Using a single-photon source, we experimentally demonstrate the counterfactual communication and successfully transfer a monochrome bitmap from one location to another by using a nested version of the quantum Zeno effect.

www.pnas.org...

If there's no wave function, how did information go from point A to point B without the transmission of a particle on the phase part of the wave function?

You said there's no photon traveling.

Tell me, when single photons are shot at the barrier in the double slit experiment and end up on the screen to form an interference pattern or behave like particles if a measuring apparatus is placed at the sides of one of the slits, how did the single photon get from the source to the back of the screen if it didn't travel?

I don't want to get sidetracked here from the thread but what you said makes no sense. If you want to replace quantum theory, I suggest you get a paper published, do experiments to confirm what you're saying, have those experiments replicated and then win a Nobel Prize.

a reply to: neoholographic

Hi again...
all you're saying is that the theory must be right because the theory says it is right.
Hell and heaven must exist because the church is telling so.
Slow down..
Just because someone says the quantum theory must be right and this quantum theory experiments proves it is right...
do you see the conflict ??
It's like the guy who stretches some blanket, put a stone on it that bends it down, and than tell people this is how gravity works.. Using gravity to explain gravity is kind of... stupid, right ??

Now think about QM. This whole thing is just a mathematical construct, nothing more. There are things like creation out of nothing, energies borrowed from the future, negative energies, virtual particles and whole other wired fairy tales stuff invented to hold the theory alive.
The universe is not like this.
You can not take five people out of the room if there are just three people inside and than say you need to put two people inside so the room is empty. The math holds, sure 3-5+2=0

Tell me, when single photons are shot at the barrier in the double slit experiment and end up on the screen to form an interference pattern or behave like particles if a measuring apparatus is placed at the sides of one of the slits, how did the single photon get from the source to the back of the screen if it didn't travel?

The term photon, is just a word needed in the theory to describe an energy level, it is not a real thing, it is a term for something else. This something else is electro magnetic radiation.
A photon, is a name for a chunk of this radiation. That is why it is also called quantised. The whole EM spectrum is continuous, but the theory need chunks for calculus, numbers are chunks, quanta... it has it in it's name

So, how EM radiation is created ??
The movement of charged particles, protons and electrons cause a change in the electric slope in the E field.
This happens all the time.
More rapid change is what you need if you want to do any experiments, right ?
What is a source for this "single photon" you say ? Charged particles ! Electrons !
SO, you move some electrons in some extreme way so that you have a bigger slope in the field, big enough to detect it by some other charged particles in your detector, otherwise you won't be able to "see" anything, right ?

Keep in mind, ALL STUFF IS MADE OF CHARGE PARTICLES !!
all sources, all walls, all receivers, you , me, the sun and everything else.
There is no WALL as you see it in the picture of the slit experiment.. a line with a hole... or two

Is the EM radiation not there before you "send the photon" ??
It is there, all the time. It is also around the billions of atoms in the wall with the slits, that one you "send the photon through"

There is no photon.. just electro magnetic wave propagating in the field. Nothing is travelling from the source to the screen where the EM wave kicks some other charged particles out of they motion... and you say, see !! there is the photon !!
NO, there is non and there was no photon.
What you see is another charged particle displaced from it's orbital by the EM wave that propagated from the source.
Propagation is not movement, it is a change in EM slope. Nothing, no matter or anything is displaced here.

I know... now you will say, there is a wave, yes, an electro magnetic wave. This is not the wave function we are talking about.
The wave function in QM, is just a mathematical construct, the real wave is way too complex to describe it with symbols.

If you have a better theory than Quantum Theory that has given us the modern world we live in and is the most accurate theory we have to date

...not sure what world you live in, my world is build with chemistry, wood, plastic, concrete and steel..

a reply to: Bandu

Look, I'm not going to spend much time debating you on this because your post is incoherent. You offer nothing but opinion without a shred of evidence to support what your saying.

Yes, I accept Quantum Theory because experiment after experiment says it's right and most of the scientific community agrees with it.

Like I said, if you have something that can refute these experiments and show that Quantum Theory is wrong, publish a paper, have experiments replicated and win a Nobel Prize.

You're saying nonsense like this is just meaningless.

Just because someone says the quantum theory must be right and this quantum theory experiments proves it is right... do you see the conflict ?? It's like the guy who stretches some blanket, put a stone on it that bends it down, and than tell people this is how gravity works.. Using gravity to explain gravity is kind of... stupid, right ??

This is just pure gobbledygook.

No, I don't see any conflict. If experiment after experiment supports Quantum Theory then why should I accept your Ted Kaczynski styled ramblings over the success of quantum theory?

Quantum mechanics has had enormous[18] success in explaining many of the features of our universe. Quantum mechanics is often the only theory that can reveal the individual behaviors of the subatomic particles that make up all forms of matter (electrons, protons, neutrons, photons, and others). Quantum mechanics has strongly influenced string theories, candidates for a Theory of Everything (see reductionism).

Quantum mechanics is also critically important for understanding how individual atoms are joined by covalent bonds to form molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. Quantum mechanics can also provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others and the magnitudes of the energies involved.[86] Furthermore, most of the calculations performed in modern computational chemistry rely on quantum mechanics.

In many aspects modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include quantum chemistry, quantum optics, quantum computing, superconducting magnets, light-emitting diodes, the optical amplifier and the laser, the transistor and semiconductors such as the microprocessor, medical and research imaging such as magnetic resonance imaging and electron microscopy.[87] Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule DNA.[88]

Many modern electronic devices are designed using quantum mechanics. Examples include the laser, the transistor (and thus the microchip), the electron microscope, and magnetic resonance imaging (MRI). The study of semiconductors led to the invention of the diode and the transistor, which are indispensable parts of modern electronics systems, computer and telecommunication devices. Another application is for making laser diode and light emitting diode which are a high-efficiency source of light.

en.wikipedia.org...

The only reason I'm debating your nonsense is because of this quarantine so why not. You said:

all you're saying is that the theory must be right because the theory says it is right.

No, I'm saying it's right because experiment after experiment after experiment says it's right. It's called Science vs. this:

The wave function in QM, is just a mathematical construct, the real wave is way too complex to describe it with symbols.

LOL, if it's too complex to describe with symbols, how do we know it exists? Is Science supposed to depend on this magical wave that's only in your mind?

I will stick with Schrodinger vs your magic wave that nobody knows about but you.

a reply to: neoholographic

You still believe in Planck time?

Maybe public disclosure is on a new page?
Things must have changed since 1958.
It was Indian physicists training in Sweden back then.

a reply to: neoholographic

as the time passes... we will see

I see you already have an opinion, quantum mechanics is the GOD !, so why did you said...

There's no need for Wave Function collapse or Measurement in Quantum Mechanics

??

if quantum mechanics is the theory of "the truth" why do you doubt the collapsing wave function ?

... I know you know the difference between a collapsing wave ( not possible ) and an collapsing function - the wave function

... I know you know, the term "Wave Function collapse" is not the same as a electro magnetic wave collapse...

you see... this term "Wave Function collapse" actually means.. the equation does not work out !!

this means at this point the theory fails !!!

a reply to: Bandu
The mathematical models in quantum mechanics do a great job of predicting what will happen in an experiment.
It's not really a "belief" that is the case, it's based on many experiments and observations.

What the model means or how to interpret it physically is up for debate, and the "wave function collapse" is only part of a possible interpretation which seems to be falling out of favor even though it's the interpretation taught in textbooks. There are other interpretations which don't involve wave function collapse and nobody has been clever enough yet to design an experiment to show which interpretation is correct.

But I think Freeman Dyson has a point about wave function collapse, or perhaps lack of it:

The Collapse Of The Wave-Function

Unfortunately, people writing about quantum mechanics often use the phrase "collapse of the wave-function" to describe what happens when an object is observed. This phrase gives a misleading idea that the wave-function itself is a physical object. A physical object can collapse when it bumps into an obstacle. But a wave-function cannot be a physical object. A wave-function is a description of a probability, and a probability is a statement of ignorance. Ignorance is not a physical object, and neither is a wave-function. When new knowledge displaces ignorance, the wave-function does not collapse; it merely becomes irrelevant.

His view may not be universal, but I think he makes a good point.

Think of it this way, if you take a frame out of a movie, does that negate the movie's existence? No, it merely means you have selected a singe momentary frame in a continuum. The continuum (or wave function) remains.

originally posted by: Krakatoa
Think of it this way, if you take a frame out of a movie, does that negate the movie's existence? No, it merely means you have selected a singe momentary frame in a continuum. The continuum (or wave function) remains.

The wave function is nothing like a movie, so that analogy isn't relevant. In a movie frame an object is either at point A or point B, not 50% probability of being at point A and 50% probability of being at point B.

If the wave function says there's a 50% chance of the object being at point A and a 50% chance of it being at point B, there's no analogy in a movie frame for that.

Only after you make an observation, do you find out if the object is at A or B, and once that happens, let's say you find the object at A, how can the wave function still exist since it says the object has a 50% chance of being at B when that's not true anymore? If the object is definitely at A after the observation, there's a 0% chance it's at B after the observation. So that analogy simply doesn't work for quantum mechanics.

a reply to: Arbitrageur

Unfortunately, people writing about quantum mechanics often use the phrase "collapse of the wave-function" to describe what happens when an object is observed. This phrase gives a misleading idea that the wave-function itself is a physical object. A physical object can collapse when it bumps into an obstacle. But a wave-function cannot be a physical object. A wave-function is a description of a probability, and a probability is a statement of ignorance. Ignorance is not a physical object, and neither is a wave-function. When new knowledge displaces ignorance, the wave-function does not collapse; it merely becomes irrelevant.

exactly !!!
any time one observe a system, one interacts with the system, so the system is changed, the "function" ( mathematical calculation ) needs to be "rewritten" to take in count the interaction.

originally posted by: Bandu
a reply to: Arbitrageur

Unfortunately, people writing about quantum mechanics often use the phrase "collapse of the wave-function" to describe what happens when an object is observed. This phrase gives a misleading idea that the wave-function itself is a physical object. A physical object can collapse when it bumps into an obstacle. But a wave-function cannot be a physical object. A wave-function is a description of a probability, and a probability is a statement of ignorance. Ignorance is not a physical object, and neither is a wave-function. When new knowledge displaces ignorance, the wave-function does not collapse; it merely becomes irrelevant.

exactly !!!
any time one observe a system, one interacts with the system, so the system is changed, the "function" ( mathematical calculation ) needs to be "rewritten" to take in count the interaction.

Yeah. Arbitrageur's post should be pinned or something.