Full Earth view from ISS Cupola Impossible 100 percent Fake

originally posted by: WaxingGibbons
a reply to: samara11278

Since the side windows sit at an ~90 degree angle to the round one, giving the cupola a "cup" shape... if you were to look out of those side windows, even though you could not see the full hemisphere of Earth from this distance, you could see black space on the outside edge of the area visible to you.

Not in a perfect sphere around a portion of Earth......

If you think about it logically, you would be able to see edges on every "side" since you have a 360 degree view. It's like if you are sitting in the front row at a movie theater - the screen takes up your whole field of vision (central round window), but if you turn your head, right, left, up, down and diagonally, then you can see the edges of the screen. If the screen was shaped like a sphere, you wouldn't be able to see the picture displaying on the hemisphere because it would be outside your field of view - but you could see the middle-ish part of the image on the edge of the sphere when turned to the side, seeing both the wall and the screen. It would appear as if it was the hemisphere from your perspective because it would look like the edge, even if it was not the true hemisphere.

a reply to: WaxingGibbons

The point of the concept is to show you how to (with math) apply refraction to any angle.

You're right that angles don't matter because my example proves refraction is possible at any angle.

=============

Elementary geometry tells us that, because the angle between the dashed lines at G is a right angle, the distance OG from the observer (O) to the horizon (G) is related to the radius R and the observer's height h by the Pythagorean Theorem:


(R + h)2= R2 + OG2
or
OG2 = (R + h)2 − R2 .
But if we expand the term (R + h)2 = R2 + 2 R h + h2, the R2 terms cancel, and we find
OG = sqrt ( 2 R h + h2 ).

It's customary to use the fact that h R at this point, so that we can neglect the second term. Then

OG ≈ sqrt ( 2 R h )
is the distance to the horizon, neglecting refraction.

The solid arc OH now represents the curved line of sight; H is the (refracted) apparent horizon. Notice that refraction lets us see a little farther, if the ray is concave toward the Earth, as shown here.

If we can assume a constant lapse rate in the air between the eye and the Earth's surface, and if the observer's height h is small compared to the 8-km height of the homogeneous atmosphere, then we can assume the curved ray is an arc of a circle. This assumption makes things easy, because the relative curvature of the ray and the Earth's surface is all that matters. In effect, we can use the previous result, but just use an effective radius of curvature for the Earth that is bigger than the real one.

This assumption is made so often that it's conventional in surveying and geodesy to use a “refraction constant” that's just the ratio of the two curvatures. A typical value of the ratio is about 1/7; that is, the ray curves about 1/7 as much as the Earth does (or, equivalently, the radius of curvature of the ray is about 7 times that of the Earth's surface).

Using this “typical” value means we should just use the formula given above, but use a value R′ instead of R for the effective radius of the Earth, where

1/R′ = 1/R − 1/(7R) = 6/(7R) ,
so that
R′ = R × 7/6 .

Arguing if this refraction is capable of showing the edges first needs to be accepted as possible. It creates a round Panorama, as Samurai put best. The fact it's round reveals none of it's very easily probable distortion. The windows literally exist to create this effect.

www.youtube.com...

Consider this video, filmed from inside the cupola module. As you can see, it's quite easy to look around and see the edges of the Earth. With a wide angle lens, you could capture all 7 angles and fit the Earth's edges in a single shot. It doesn't need to be a composite shot. It's not fake, simple as that.

a reply to: tigertatzen

He's denying refraction even EXISTS. You wouldn't be WRONG if he wasn't so WRONG.

a reply to: samara11278

No, from 450 km you can only see about 4700 km of the surface, so there is no way you would see space around the edges of this area, at all, in fact, since space is not next to this area, there is more surface next to this area. The Earth would simply fill up the whole cupola up to the frame, especially with the pics I posted which are taken from deeper inside the cupola, about 2 m from the windows.

Again, from 450 km you simply cannot see more than around 4700 km of the surface......

With an Fish I lens I CAN make the Shot



With and Without glass in the windows

But now there is distortion of the edges of the windows, they round up.

originally posted by: WaxingGibbons
a reply to: samara11278

No, from 450 km you can only see about 4700 km of the surface, so there is no way you would see space around the edges of this area, at all, in fact, since space is not next to this area, there is more surface next to this area. The Earth would simply fill up the whole cupola up to the frame, especially with the pics I posted which are taken from deeper inside the cupola, about 2 m from the windows.

Again, from 450 km you simply cannot see more than around 4700 km of the surface......

But when looking out of the SIDE windows that are not facing the earth directly, but are almost perpendicular to it, you are viewing at an angle skirting the edge of the front field of view. it doesn't matter how close you are to something, if you look 90 degrees left/right/up/down, you will see the surroundings as long as the object isn't concave and curving around you.

a reply to: EartOccupant

You can't view the entire Earth from 450 km, there simply is no line of sight. Again, it has been proven over and over again and even NASA says it is not possible.

We also established that these pics show only a portion of the Earth, so why does a portion of the Earth look like a perfect sphere with space all around it?

Hold a basketball in front of your face close enough that you cannot see anything but the basketball. Now turn your head to either side.

Naw I have actually identified the problem with the official shot

They shoulda just said it's a facsimile, huh!

Coz ATS just takes this stuff apart, we're so smart, so modern

Now also the thickness of the panes, up for your conjecture....no longer merely the angle of the perimeter window panes....now we introduce the thickness

Can I have a nice round of applause, please...thank you....thank you....''tis nothing for a stepper

Radio edit.... and throw in a star somebody!......he....he

a reply to: Shamrock6

Yes I think you are right...a flat Earther who is distraught and discouraged by factual information.

originally posted by: EartOccupant
With an Fish I lens I CAN make the Shot



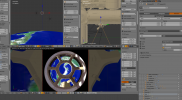
With and Without glass in the windows

But now there is distortion of the edges of the windows, they round up.

Nice job simulating it in blender.

a reply to: WaxingGibbons

Hey, i'm just trying to visualize your quest.

a reply to: samara11278

The camera position is 2m from the windows, so your field of view is limited by the 2m diameter, no matter what. And again, you simply can't view the entire Earth from 450 km up, NASA says this themselves, and a simple diagram shows this.

a reply to: samara11278

The camera is not turned to the side, it is looking straight through the middle of the cupola, from 2m inside the cupola......

I starred ya samara....let's trade stars....

Oh wait this about a planet.....my bad

a reply to: MacK80

I did not deny such a thing, the values I used for my calculation were even corrected for refraction, I used Metabunks calculator.

a reply to: WaxingGibbons

Hey. look at the solar panel carefully....why is it curving? like its distorted a bit due to refraction. I use photoshop and also take pictures. Depending on the lenses used you can see more than other times. this window has specialized glass/panes to enable observation and pictures apparently.

IS this th esame place in both pictures... if so... why does the stuff outside of it change posistion? COuld they be Photoshopped in? That or its a DIFFERENT VIEWPORT each time. Op thats really clever of you.

a reply to: EartOccupant

Well, you are doing something wrong because it is not possible to view the entire Earth from 450 km, and again, we already established that it shows a portion of the Earth as a sphere with space all around it.

Yes, two meters.....I figured about that, you are right, the cupola would have to be almost half the space station to get the shot

See, WaxingGibbons has judgement.....so hard to come across these days

Hey WaxingGibbons....we need ya over at the pentagon accident scene thread really badly

a reply to: WaxingGibbons